Conductance & its Applications | Physical Chemistry PDF Download
| Table of contents |

|
| Conductance |

|
| Variation of Conductance with Dilution |

|
| Application of Kohlrausch’s Law |

|
| (i) Determination of Molar Conductivity of a Weak Electrolyte |

|
| Transport Number |

|
Conductance
Conductance is the ability of a substance to conduct electric current. It is the reciprocal of resistance, meaning that the higher the conductance, the lower the resistance to electric flow.
Formula
The conductance (G) of an electrolytic solution can be expressed as:
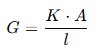
where:
- G = Conductance (measured in siemens, S)
- K = Specific conductance or conductivity of the solution (S/m)
- A = Area of cross-section of the electrodes (m²)
- l = Distance between the electrodes (m)
Specific Conductance
Specific conductance (K) is defined as the conductance of a solution when the distance between electrodes is 1 cm and the area of the electrodes is 1 cm². It is a measure of how well the solution conducts electricity due to the movement of free ions.
Unit: The unit of specific conductance is S/m (siemens per meter) or Ω−1 (ohm inverse).
Molar Conductance (Λ)
Molar conductance refers to the conductance of all the ions produced by one mole of an electrolyte in solution. It can be expressed as:

where:
- Λ = Molar conductance (Ω⁻¹ cm² mol⁻¹)
- G = Conductance of the solution (S)
- C_m = Concentration of the solution in terms of molarity (mol/L)
SI Unit: Molar conductance is expressed in S m² mol⁻¹.
Equivalent Conductance (Λ_eq)
Equivalent conductance is the conducting power of all the ions produced by one gram-equivalent of an electrolyte in a solution. It is defined similarly to molar conductance but based on equivalents rather than moles.
Unit: Equivalent conductance is measured in S cm² equiv⁻¹.
Relationship Between Molar and Equivalent Conductivities
The relationship can be expressed as:
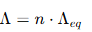
where: n = number of equivalents of the electrolyte, representing the total charge carried by the ions.
Variation of Conductance with Dilution
- Specific Conductance (K) decreases with dilution because the volume of the solution increases more than the number of ions present, leading to fewer ions per unit volume.
- Equivalent Conductance (Λ_eq) and Molar Conductance (Λ) increase with dilution due to a higher degree of dissociation and greater ionic mobility in less concentrated solutions.
Theories Explaining Conductance Changes
1. Arrhenius Theory of Electrolytic Dissociation
- Concept: Proposed by Svante Arrhenius, this theory posits that electrolytes dissociate into ions when dissolved in water. The extent of this dissociation varies with the electrolyte's strength (strong vs. weak).
- Dissociation Equation:
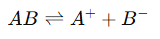
- Equilibrium Constant:
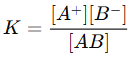
- Degree of Dissociation (α): For weak electrolytes, the degree of dissociation increases with dilution, leading to an increase in the number of ions in the solution. This contributes to an increase in conductance.
2. Ostwald Dilution Law
- Concept: This law describes the relationship between the degree of dissociation (α) and concentration (c) for weak electrolytes. It states that as the concentration of a weak electrolyte decreases, the degree of dissociation increases.
- Formula:
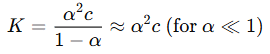
- Application: This theory helps explain why molar conductance increases with dilution for weak electrolytes, as more ions contribute to conductance.
3. Debye-Hückel Theory
- Concept: This theory provides a quantitative description of the behavior of ions in solution. It accounts for the interactions between ions, known as the ionic atmosphere.
- Ionic Atmosphere: Each ion is surrounded by oppositely charged ions, which can affect its mobility. When an electric field is applied, this atmosphere becomes distorted, impacting the ion's movement.
- Effect on Conductance: The mobility of ions decreases due to the asymmetric effect and the electrophoretic effect:
- Asymmetric Effect: Ions experience uneven forces due to the distortion of their ionic atmosphere when an electric field is applied.
- Electrophoretic Effect: Ions carry solvent molecules with them, and the motion of these solvent molecules can oppose the movement of the ions.
4. Debye-Hückel-Onsager Equation
- Concept: This equation extends the Debye-Hückel theory and provides a model for calculating molar conductance of strong electrolytes at low concentrations.
- Equation:

Explanation: This equation captures the decrease in conductance due to the effects of ion interactions as the concentration of the electrolyte changes.
5. Ionic Mobility
- Concept: Ionic mobility refers to the speed at which ions move through a solution when an electric field is applied. It is a key factor in determining conductance.
- Effect of Dilution: As the solution is diluted, ionic mobility increases for both weak and strong electrolytes:
- Weak Electrolytes: Increased dissociation leads to more ions, enhancing overall conductance.
- Strong Electrolytes: Decreased inter-ionic attractions allow ions to move more freely, increasing mobility and, consequently, conductance.
Kohlrausch’s Law
Kohlrausch's Law states that the molar conductivity of an electrolyte at infinite dilution is equal to the sum of the contributions of the individual ions produced by the electrolyte. This law is significant because it allows us to understand the behavior of electrolytes in solution, particularly at very low concentrations where interactions between ions become negligible.
Formula
Kohlrausch's Law can be mathematically expressed as: At infinite dilution, the molar conductivity of an electrolyte can be expressed as the sum of contributions from its individual ions:
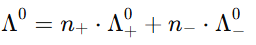
where:
- Λ0 = molar conductivity at infinite dilution
- n+ = number of cations
- n- = number of anions
- Λ+0 and Λ-0 = molar conductivities of the cation and anion at infinite dilution.
Application of Kohlrausch’s Law
(i) Determination of Molar Conductivity of a Weak Electrolyte
To calculate the molar conductivity () of a weak electrolyte like acetic acid (), we can use known conductivities of strong electrolytes that share common ions.
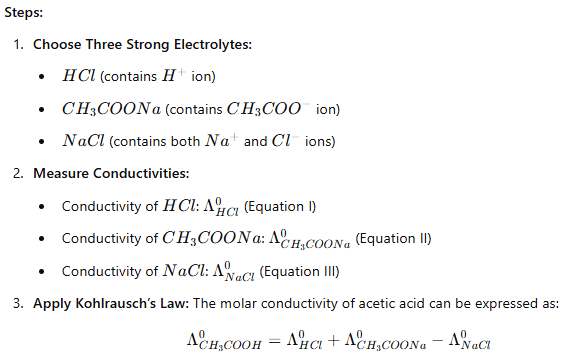
Proof of the Equation:
From Equations I, II, and III:

Adding Equation I and Equation II and then subtracting Equation III will yield the molar conductivity of acetic acid.
(ii) Determination of Degree of Dissociation (α)
The degree of dissociation (α) indicates how much of the weak electrolyte dissociates into ions in a solution. It can be determined using the relationship between molar conductivity and concentration.
Formula:
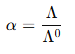
where:
- = observed molar conductivity at a specific concentration.
- = molar conductivity at infinite dilution.
(iii) Determination of Solubility of Sparingly Soluble Salts
For a sparingly soluble salt, the solubility (S) can be determined using its molar conductivity.
Example: For a salt like , the molar conductivity can be used to relate to its solubility in water, leading to an expression for .
(iv) Determination of Ionic Product of Water
The ionic product of water () is defined as the product of the molar concentrations of the hydrogen ions and hydroxide ions
[OH−]:
Formula:
At 25°C, is approximately
Transport Number
The transport number is a dimensionless quantity that represents the fraction of the total electric current carried by each type of ion in an electrolyte solution. It helps to quantify how effectively each ion contributes to the overall conductivity of the solution.
Importance
Understanding the transport number is essential in electrochemistry because it provides insights into:
- The mobility of ions within the solution.
- The efficiency of electrolysis processes.
- The behavior of electrolytes in various concentrations.

Calculation
The transport number can be defined mathematically for cations and anions as follows:
- For cation:

- For anion:
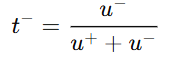
where:
- u+ = mobility of cation
- u- = mobility of anion
Since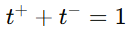 , knowing the transport number of one ion allows for the calculation of the other.
, knowing the transport number of one ion allows for the calculation of the other.
|
84 videos|142 docs|67 tests
|
FAQs on Conductance & its Applications - Physical Chemistry
| 1. What is conductance and how is it measured ? |  |
| 2. How does dilution affect the conductance of an electrolyte solution ? |  |
| 3. What is Kohlrausch’s Law and how is it applied to determine molar conductivity ? |  |
| 4. How can the molar conductivity of a weak electrolyte be determined experimentally ? |  |
| 5. What are transport numbers and why are they important in the study of conductance ? |  |
















