Conduction: One Dimensional - 1 | Heat Transfer - Mechanical Engineering PDF Download
Conduction: One Dimensional, Heat Transfer
The fundamentals of heat conduction were established over one and a half century and its contribution goes to a French mathematician and physicist, Jean Baptiste Joseph Fourier. You may be aware that any flow whether it is electricity flow, fluid flow, or heat flow needs a driving force. The flow is proportional to the driving force and for various kinds of flows the driving force is shown in the table 2.1.
Table 2.1. Various flows and their driving forces
Thus the heat flow per unit area per unit time (heat flux,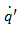 ) can be represented by the following relation,
) can be represented by the following relation,
(2.1)
(2.2)
where, proportionality constant k is the thermal conductivity of the material, T is the temperature and x is the distance in the direction of heat flow. This is known as Fourier’s law of conduction.
The term steady-state conduction is defined as the condition which prevails in a heat conducting body when temperatures at fixed points do not change with time. The term one-dimensional is applied to a heat conduction problem when only one coordinate is required to describe the distribution of temperature within the body. Such a situation hardly exists in real engineering problems. However, by considering one-dimensional assumption the real problem is solved fairly upto the accuracy of practical engineering interest.
2.1 Steady-state conduction through constant area
A simple case of steady-state, one-dimensional heat conduction can be considered through a flat wall as shown in the fig.2.1.
Fig.2.1: Steady-state conduction through a slab (constant area)
The flat wall of thickness dx is separated by two regions, the one region is at high temperature (T1 ) and the other one is at temperature T2 . The wall is very large in comparison of the thickness so that the heat losses from the edges are negligible. Consider there is no generation or accumulation of the heat in the wall and the external surfaces of the wall are at isothermal temperatures T1 and T2 . The area of the surface through which the heat transfer takes place is A. Then the eq.2.2 can be written as,
(2.3)
(2.4)
(2.5)
The negative sign shows that the heat flux is from the higher temperature surface to the lower temperature surface and is the rate of heat transfer through the wall.
Now if we consider a plane wall made up of three different layers of materials having different thermal conductivities and thicknesses of the layers, the analysis of the conduction can be done as follows.
Consider the area (A) of the heat conduction (fig.2.2) is constant and at steady state the rate of heat transfer from layer-1 will be equal to the rate of heat transfer from layer-2. Similarly, the rate of heat transfer through layer-2 will be equal to the rate of heat transfer through layer-3. If we know the surface temperatures of the wall are maintained at T1 and T2 as shown in the fig.2.2, the temperature of the interface of layer1 and layer 2 is assumed to be at T' and the interface of layer-2 and layer-3 as T".
Fig.2.2: Heat conduction through three different layers
The rate of heat transfer through layer-1 to layer-2 will be,
and,
The rate of heat transfer through layer 2 to layer 3 will be,
and,
The rate of heat transfer through layer 3 to the other side of the wall,
On adding the above three equations,
(2.9)
(2.10)
Where, R represents the thermal resistance of the layers. The above relation can be written analogous to the electrical circuit as,
Fig 2.3: Equivalent electrical circuit of the fig.2.2
The wall is composed of 3-different layers in series and thus the total thermal resistance was represented by R (= R1 + R2 + R3 ). The discussed concept can be understood by the illustrations shown below.
The unit of the various parameters used above is summarized as follows,
|
55 videos|100 docs|86 tests
|
FAQs on Conduction: One Dimensional - 1 - Heat Transfer - Mechanical Engineering
| 1. What is one-dimensional conduction in chemical engineering? |  |
| 2. How is heat transferred in one-dimensional conduction? |  |
| 3. What factors affect the rate of one-dimensional conduction? |  |
| 4. How is one-dimensional conduction mathematically described? |  |
| 5. What are some applications of one-dimensional conduction in chemical engineering? |  |





















