Conservation of Momentum & Equilibrium of a Particle | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
What is Conservation of Momentum?
Conservation of momentum is a major law of physics which states that the momentum of a system is constant if no external forces are acting on the system. It is embodied in Newton’s First Law or The Law of Inertia. The law of conservation of momentum is generously confirmed by experiment and can even be mathematically deduced on the reasonable presumption that space is uniform.
Conservation of Linear Momentum
Conservation of linear momentum is based on Newton’s second law of motion which states that in an isolated system the total momentum remains the same. Let’s consider the following example,
Remember: In the above experiment we did not consider any loss of energy due to friction, heat, etc. and all the collisions were elastic in nature i.e. there was a total transfer of energy, Actual observations may differ.
Let’s consider a case where a football of mass M2 is resting on the ground, a bowling ball with a comparatively heavier mass of M1 is thrown at the football at a velocity of U1.
When the bowling ball hits the football the energy is transferred and the bowling ball loses some velocity and moves at a new velocity V1, the football moves at velocity V2, why did the football move?
To conserve linear momentum, i.e. the bowling ball had an initial momentum of M1 so as M2 < M1 and the momentum of football should be equal to the momentum lost by the bowling ball according to the law of conservation of momentum, the football had no other option than moving at a velocity V2.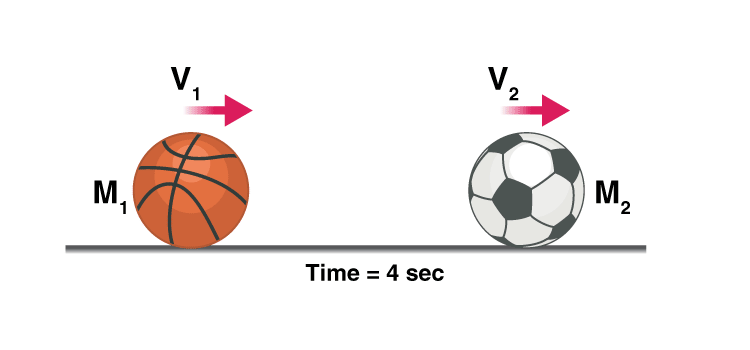
Formula
Mathematically it is given by,
m1u1 + m2u2 = m1v1 + m2v2
Note: m1u1 ≠ m1v1
Where,
m1 is mass of the bowling ball
m2 is the mass of the football
u1 and u2 are the initial velocities and v1 and v2 are the final velocities.
Even though the momentum of each particle changes, altogether the momentum of the system remains constant as long as there is no external force acting on it. In a head-to-head car accident, the momentum is transferred from one car to the other, but so much force is applied that the car structure cannot handle it, this is why a car wrecks. If the cars were able to deal with the amount of force, and the collision was elastic they both will move in opposite directions, considering their weights are the same.
In short, momentum is always conserved in any collision, whether it be an elastic or a non-elastic collision, though kinetic energy is not conserved in a non-elastic collision, the kinetic energy is converted into heat energy or potential energy, etc.
Example of Conservation Of Momentum
Consider this example of a balloon, the particles of gas move rapidly colliding with each other and the walls of the balloon, even though the particles themselves move faster and slower when they lose or gain momentum when they collide, the total momentum of the system remains the same.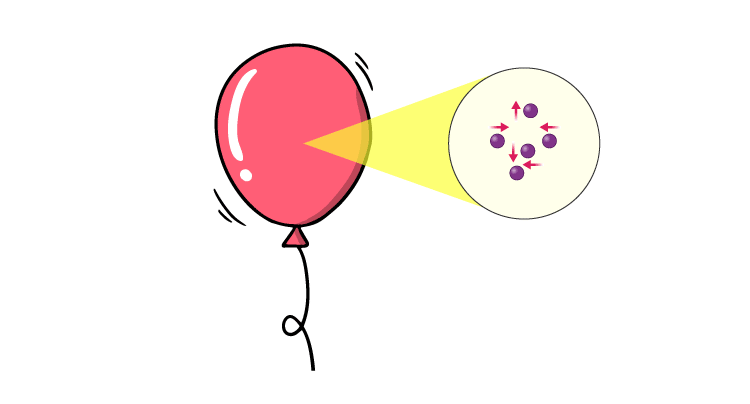 Hence, the balloon doesn’t change in size, if we add external energy by heating it, the balloon should expand because it increases the velocity of the particles and this increases their momentum, in turn, increasing the force exerted by them on the walls of the balloon.
Hence, the balloon doesn’t change in size, if we add external energy by heating it, the balloon should expand because it increases the velocity of the particles and this increases their momentum, in turn, increasing the force exerted by them on the walls of the balloon.
Application of Law of Conservation of Momentum
Having said so the energy of a system is always conserved, one of the best applications of the law of conservation of momentum would be in space travel, there is no medium in space to exert a force on, then how do rockets travel?
Well, they eject matter at very high speed so in an isolated system the momentum should remain constant therefore the rocket will move in the opposite direction with the same momentum as that of the exhaust.
Equilibrium
Forces which have zero resultant and zero turning effect will not cause any change in the motion of the object to which they are applied. Such forces (and the object) are said to be in equilibrium. For understanding the equilibrium of an object under two or more concurrent or coplanar forces let us first discuss the resolution of force and moment of a force about some point.
➢ Resolution of a Force
When a force is replaced by an equivalent set of components, it is said to be resolved. One of the most useful ways in which to resolve a force is to choose only two components (although a force may be resolved in three or more components also) which are at right angles also. The magnitude of these components can be very easily found using trigonometry.
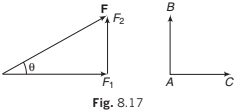
In Fig. 8.17, F1 = F cos θ = component of F along AC.
F2 = F sin θ = component of F perpendicular to AC AB.
Finding such components is referred to as resolving a force in a pair of perpendicular directions.
Note: that the component of a force in a direction perpendicular to itself is zero. For example, if a force of 10 N is applied on an object in horizontal direction then its component along vertical is zero. Similarly, the component of a force in a direction parallel to the force is equal to the magnitude of the force. For example component of the above force in the direction of force (horizontal) will be 10 N.
In the opposite direction the component is −10 N.
➤ Example 8.4 Resolve a weight of 10 N in two directions which are parallel and
perpendicular to a slope inclined at 30° to the horizontal.
Solution: Component perpendicular to the plane
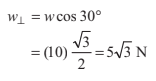
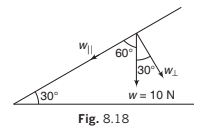
and component parallel to the plane

➤ Example 8.5 Resolve horizontally and vertically a force F N = 8 which makes
an angle of 45° with the horizontal.
Solution Horizontal component of F is

= 4√2 N
and vertical component of F is FV = ° sin 45
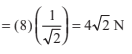
➤ Example 8.6 A body is supported on a rough plane inclined at 30° to the horizontal by a string attached to the body and held at an angle of 30° to the plane. Draw a diagram showing the forces acting on the body and resolve each of these forces
(a) horizontally and vertically,
(b) parallel and perpendicular to the plane.
Solution. The forces are:
(i) The tension in the string T
(ii) The normal reaction with the plane N
(iii) The weight of the body w and the friction f
(a) Resolving horizontally and vertically
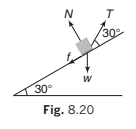
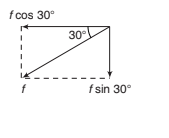
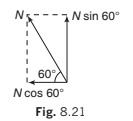

Resolving horizontally and vertically in the senses OX and OY as shown, the components are

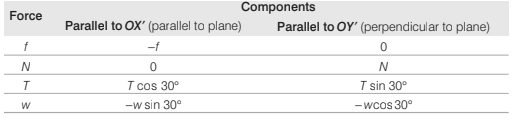
(b) Resolving parallel and perpendicular to the plane
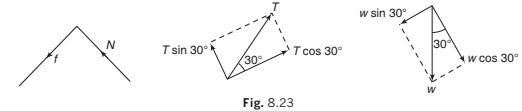
Resolving parallel and perpendicular to the plane in the senses OX ′ and OY ′ as shown, the components are :
➢ Moment of a Force
The general name given to any turning effect is torque. The magnitude of torque, also known as the moment of a force F is calculated by multiplying together the magnitude of the force and its perpendicular distance  from the axis of rotation. This is denoted by C or π (tau). i.e
from the axis of rotation. This is denoted by C or π (tau). i.e

➢ Direction of Torque
The angular direction of a torque is the sense of the rotation it would cause.
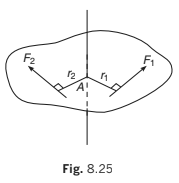
Consider a lamina that is free to rotate in its own plane about an axis perpendicular to the lamina and passing through a point A on the lamina. In the diagram the moment about the axis of rotation of the force F1 is F1 r1 anticlock-wise and the moment of the force F2
is F2r2 clockwise. A convenient way to differentiate between clockwise and anticlock-wise torques is to allocate a positive sign to one sense (usually, but not invariably, this is anticlockwise) and negative sign to the other. With this convention, the moments of F1
and F2 are + F1r1 and −F2 r2 (when using a sign convention in any problem it is advisable to specify the chosen positive sense).
➢ Zero Moment
If the line of action of a force passes through the axis of rotation, its perpendicular distance from the axis is zero. Therefore, its moment about that axis is also zero.
Note: Later in the chapter of rotation we will see that torque is a vector quantity.
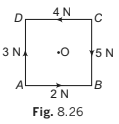
➤ Example 8.7 ABCD is a square of side 2 m and O is its centre. Forces act along the sides as shown in the diagram.
Calculate the moment of each force about
(a) an axis through A and perpendicular to the plane of square.
(b) an axis through O and perpendicular to the plane of square.
Solution. Taking anticlockwise moments as positive we have:

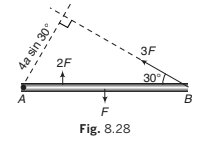
➤ Example 8.8 Forces act as indicated on a rod AB which is pivoted at A. Find
the anticlockwise moment of each force about the pivot.

Solution.

|
199 videos|422 docs|281 tests
|
FAQs on Conservation of Momentum & Equilibrium of a Particle - Physics for Airmen Group X - Airforce X Y / Indian Navy SSR
| 1. What is the conservation of momentum? |  |
| 2. How is momentum defined? |  |
| 3. What is the significance of the conservation of momentum? |  |
| 4. Can momentum be lost in a collision? |  |
| 5. How does conservation of momentum relate to equilibrium? |  |

|
Explore Courses for Airforce X Y / Indian Navy SSR exam
|

|

















