Conservation of momentum | Basic Physics for IIT JAM PDF Download
Newton's second law in its most general form, says that the rate of a change of a particle’s momentum p is given by the force acting on the particle; i.e., F = dp/dt. If there is no force acting on the particle, then, since dp/dt = 0, p must be constant, or conserved. This observation is merely a restatement of Newton’s first law, the principle of inertia: if there is no force acting on a body, it moves at constant speed in a straight line.
Now suppose that an external agent applies a force Fa to the particle so that p changes according to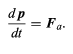 (56)
(56)
According to Newton’s third law, the particle must apply an equal and opposite force −Fa to the external agent. The momentum pa of the external agent therefore changes according to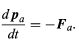 (57)
(57)
Adding together equations (56) and (57) results in the equation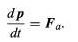 (56)
(56)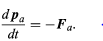 (57)
(57)
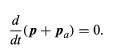 (58)
(58)
The force applied by the external agent changes the momentum of the particle, but at the same time the momentum of the external agent must also change in such a way that the total momentum of both together is constant, or conserved. This idea may be generalized to give the law of conservation of momentum: in all the interactions between all the bodies in the universe, total momentum is always conserved.
It is useful in this light to examine the behaviour of a complicated system of many parts. The centre of mass of the system may be found using equation (55). Differentiating with respect to time gives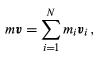 (59)
(59)
where v = dR/dt and vi = dri/dt. Note that mivi is the momentum of the ith part of the system, and mv is the momentum that the system would have if all its mass (i.e., m) were concentrated at its centre of mass, the point whose velocity is v. Thus, the momentum associated with the centre of mass is the sum of the momenta of the parts.
Suppose now that there is no external agent applying a force to the entire system. Then the only forces acting on the system are those exerted by the parts on one another. These forces may accelerate the individual parts. Differentiating equation (59) with respect to time gives (59)
(59)
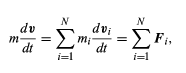 (60)
(60)
where Fi is the net force, or the sum of the forces, exerted by all the other parts of the body on the ith part. Fi is defined mathematically by the equation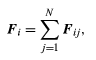 (61)
(61)
where Fij represents the force on body i due to body j (the force on body idue to itself, Fii, is zero). The motion of the centre of mass is then given by the complicated-looking formula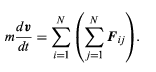 (62)
(62)
This complicated formula may be greatly simplified, however, by noting that Newton’s third law requires that for every force Fij exerted by the jth body on the ith body, there is an equal and opposite force −Fij exerted by the ith body on the jth body. In other words, every term in the double sum has an equal and opposite term. The double summation on the right-hand side of equation always adds up to zero. This result is true regardless of the complexity of the system, the nature of the forces acting between the parts, or the motions of the parts. In short, in the absence of external forces acting on the system as a whole, mdv/dt = 0, which means that the momentum of the centre of mass of the system is always conserved. Having determined that momentum is conserved whether or not there is an external force acting, one may conclude that the total momentum of the universe is always conserved.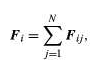 (61)
(61)
|
217 videos|156 docs|94 tests
|
FAQs on Conservation of momentum - Basic Physics for IIT JAM
| 1. What is the conservation of momentum? |  |
| 2. How is momentum defined? |  |
| 3. Can momentum be transferred between objects? |  |
| 4. What is an example of the conservation of momentum in everyday life? |  |
| 5. Does the conservation of momentum apply to all types of collisions? |  |
















