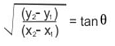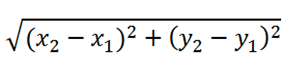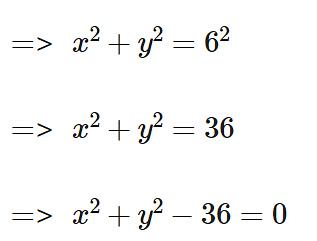Important Formulas for CAT Coordinate Geometry
| Table of contents |

|
| Introduction |

|
| Coordinate Geometry Formulae |

|
| Equations of a Line |

|
| Solved Examples |

|
Introduction
Coordinate Geometry holds significant importance in many competitive exams such as CAT Quantitative Ability (QA) section. Typically, problems in Coordinate Geometry are not overly challenging, making it crucial not to overlook them. Practicing a sufficient number of Coordinate Geometry questions enhances your ability to tackle such problems effortlessly during the actual exam. In this article, we will delve into essential Coordinate Geometry questions for QA, offering valuable practice.
- A coordinate graph is a rectangular grid with two number lines called axes. The x-axis is the horizontal number line and the y-axis is the vertical number line.
- The axes intersect at the origin which is the point (0,0).

- Coordinate geometry is used to describe various curves such as circles, parabolas, etc.
- Coordinate geometry divides the coordinate plane into four different quadrants, which are the I quadrant, II quadrant, III quadrant, and IV quadrants.
Coordinate Geometry Formulae
1. Distance Formula
To Calculate Distance Between Two Points:
Let the two points be A and B, having coordinates to be (x1, y1) and (x2, y2) respectively.
Thus, the distance between two points is-
distance =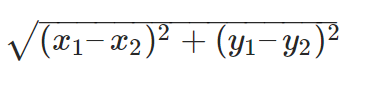
Example: Find the distance between the points (5,2) and (3,4)?
Sol: Using distance formula,
Distance = √(5-3)2 + (2-4)2
= 2√2 units
2. Midpoint Theorem
To Find Mid-point of a Line Connecting Two Points:
Consider the same points A and B, having coordinates to be (x1, y1) and (x2, y2) respectively. Let M(x,y) be the midpoint of lying on the line connecting these two points A and B. The coordinates of this point are –
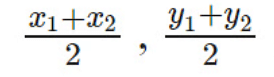
3. Angle Formula
To Find the Angle Between Two Lines:
Consider two straight lines and, with given slopes as m1 and m2 respectively.
Let “θ” be the angle between these two lines, we can then represent the angle between them as-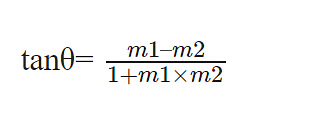
4. Section Formula
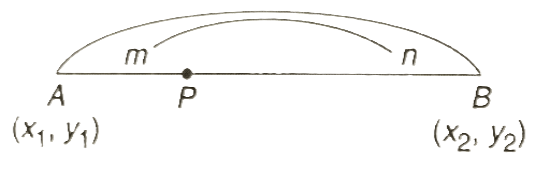 To Find a Point which divides a line into m:n ratio: Consider two straight lines having coordinates (x1, y1) & (x2, y2) respectively.
To Find a Point which divides a line into m:n ratio: Consider two straight lines having coordinates (x1, y1) & (x2, y2) respectively. Let a point which divides the line in some ratio as m:n, then the coordinates of this point are-
(i) When the ratio m:n is internal:
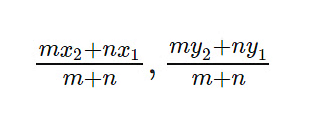
(ii) When the ratio m:n is external:
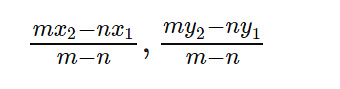
Example: Find the point which divides the line segment joining (2,5) and (1,2) in ratio 2:1 internally?
Sol: Using mid point theorem,
x = (2 x1 + 1x2) / (1+2)
= 4/3
y = (2x2+1x5)/ (2+1)
= 9/3 = 3
5. Area of a Triangle in Cartesian Plane
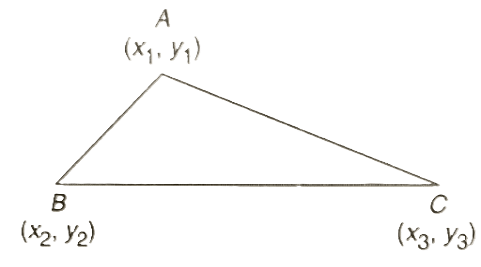 We can compute the area of a triangle in Cartesian Geometry if we know all the coordinates of all three vertices. If coordinates are (x1,y1),(x2,y2) and (x3,y3) then area will be:
We can compute the area of a triangle in Cartesian Geometry if we know all the coordinates of all three vertices. If coordinates are (x1,y1),(x2,y2) and (x3,y3) then area will be:
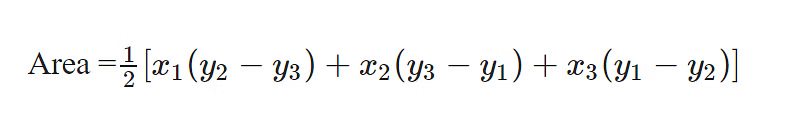
Example: Find the area of triangle (0,4) , (3,6) and (-8,-2)?
Sol: Area of triangle = I1/2 { 0(6 -(-2)) + 3((-2) - 4) + (-8)(4-6)}I
= I1/2 (-2)I
= I-1I
= 1 sq. unit
6. Centroid of a Triangle
 If G (x, y) is the centroid of triangle ABC, A (x1, y1), B (x2, y2), C (x3, y3), then:
If G (x, y) is the centroid of triangle ABC, A (x1, y1), B (x2, y2), C (x3, y3), then:

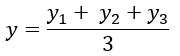
7. In-Center of a Triangle
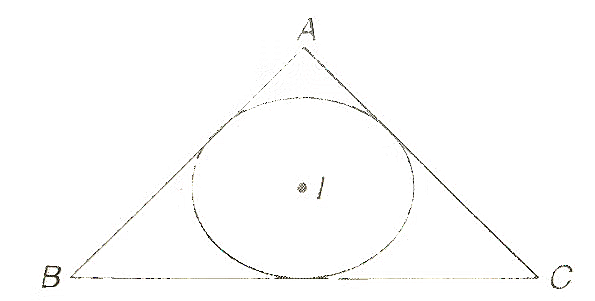
If I (x, y) is the in-center of triangle ABC, A (x1, y1), B (x2, y2), C (x3, y3), then,
where a, b and c are the lengths of the BC, AC and AB respectively
Example: Find the incenter of the right angled isosceles triangle having one vertex at the origin and having the other two vertices at (6,0) and (0,6)?
Sol:
As it is mentioned in the question that the triangle is an isosceles triangle ,therefore the sides AB = BC = 6 units and the length of the third side = (62 + 62)1/2
hence, a = c = 6 units, b = 6√2 units
In Centre will be at
→ (6x0 + 6√2 x0 + 6 x 6)/(6+6+6√2) , (6x6 + 6√2 x0 + 6 x 0)/(6+6+6√2)
→ 36/ 12+6√2 , 36/ 12+6√2
Now, let us have a look at some more formulas for coordinate geometry. We will use the below picture as a reference for the formulas.
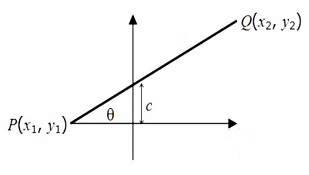
- Slope of PQ = m =

- Equation of PQ is as below:
 or y = mx + c
or y = mx + c - The product of the slopes of two perpendicular lines is –1.
- The slopes of two parallel lines are always equal.
If m1 and m2 are slopes of two parallel lines, then m1=m2. - The distance between the points (x1, y1) and (x2, y2) is

- If point P(x, y) divides the segment AB, where A (x1, y1) and B (x2, y2), internally in the ratio m: n, then,
x= (mx2 + nx1)/(m+n) and y= (my2 + ny1)/(m+n) - The equation of a straight line is y = mx + c, where m is the slope and c is the y-intercept (tan = m, where is the angle that the line makes with the positive X-axis).
- If two intersecting lines have slopes m1 and m2 then the angle between two lines θ will be tan θ = (m1−m2) / (1+m1m2)
- The length of perpendicular from a point (x1 ,y1 ) on the line AX+BY+C = 0 is
P = (Ax1+By1+C) / (A2+B2)
Equations of a Line
Let us learn all the straight lines formulas along with the general equation of a line and different forms to find the equation of a straight line in detail here.- General equation of a line Ax + By = C
- Slope intercept form y = mx + c (c is y intercept)
- Point-slope form y – y1 = m (x – x1) (m is the slope of the line)
- Intercept form x / a + y / b = 1 (where a and b are x and y intercepts respectively)
- Two point form: (y−y1) / (y2−y1) = (x−x1) / (x2−x1)
Solved Examples
Example 1: What is the distance between the points A (3,8) and B(-2,-7) ?a) 5√2
b) 5
c) 5√10
d) 10√2
Ans: Option 'c' is correct
Sol: The distance between 2 points (x1, y1) and (x2, y2) is given as
√((x2-x1)2 + (y2-y1)2)
Hence, required distance = √((-2-3)2 + (-7-8)2) = 5√10
Example 2: The points of intersection of three lines 2X + 3Y – 5=0 and 5X – 7Y + 2=0 and 9X – 5Y – 4 = 0
a) Form a triangle
b) Are on lines perpendicular to each other
c) Are on lines parallel to each other
d) Are coincident
Sol: To solve the question above, we should remember the properties of the lines for being parallel, perpendicular or intersecting:
Two lines are parallel to each other if their slopes are equal
Two lines are perpendicular if the product of slopes is -1.
Lines are coincident if they at least have one point which satisfies all the equation.
The three lines can be expressed in the y=mx + c format as:
Y = (5/3) – (2X/3), Y = (5X/7) + (2/7) , Y = (9X/5) – (4/5)
Therefore, the slopes of the three lines are -2/3, 5/7, 9/5 and their Y intercepts are 5/3, 2/7 and 4/5 respectively.
We see above that the product of slopes of none of the lines is -1. Thus, lines are not perpendicular to each other.
Also, slopes of the no two lines is same. Thus, lines are not parallel to each other.
Solving the first two equations we get X=1 and Y = 1. If we substitute (1,1) in the third equation Y=(9X/5 – 4/5), we find that it also satisfies the equation. This shows that the three lines intersect at a common point and hence coincident.
Example 3: The area of the triangle whose vertices are (a + 1, a + 1), (a, a) and (a+2, a) is
a) a3
b) 1
c) 2a
d) 21/2
Ans: Option 'b' is correct
Sol: Let a = 0, Thus the three vertices of the triangle becomes (1, 1) (0, 0) and (2, 0)
If we look at the below figure, Area = ½ * base * height = ½ * 2 * 1 = 1
Imp: The main point to note here is that area will be independent of a.
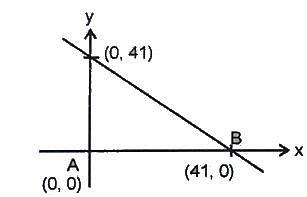
Example 4: Consider a triangle drawn on the X – Y plane with its three vertices of (41,0) , (0,41) and (0,0), each vertex being represented by its (X,Y) coordinates. The number of points with integer coordinates inside the triangle (excluding all the points on the boundary) is:
a) 780
b) 800
c) 740
d) 830
Ans: Option 'a' is correct
Sol: Equation of the line will be of the form => x + y = 41.
Now, we know that if the x,y coordinates of a point are integer, the sum will also be an integer x+ y = k (k, a variable)
As per the question we need to exclude all the values lying on the boundary of triangle, k can take all values from 1 to 40 only. K = 0 is rejected as at k =0 will give the point at A which is also not allowed.
With K = 40, x + y = 40; this will be satisfied by points (1, 39), (2, 38), (3,37) …… (38, 2), (39, 1). That is a total of 39 points
Similarly x + y = 38, will be satisfied by 37 points.
X + Y = 37, will be satisfied by 36 points
X + Y = 3 will be satisfied by 2 points
X + Y = 2 will be satisfied by 1 point
X + Y = 1 will not be satisfied by any pointSo, the total number of all such points is: 39 + 38 + 37 + 36 + ……………………. + 3 + 2 + 1 = n(n+1)/2 points = (39*40) / 2 = 780 points
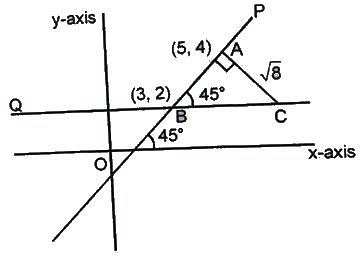
Example 5: Two lines P and Q intersect at point (3, 2) in the x-y plane. The slope of line P is 45 degrees and line Q is parallel to the X axis. What is the area (in sq. units) of the triangle formed by P, Q and a line perpendicular to P passing through point (5, 4) ?
a) 12
b) 8
c) 6
d) 4
Ans: Option 'd' is correct
Sol: Let us look at the image below:
As slope of line P is 45 degree. Therefore, ∠ABC = 45 degree
In triangle ABC, length of AB = SQRT [(5-3)2 + (4-2)2] = 2√2 units
Therefore, length of line AC = 2√2 units (Since ABC is an isosceles triangle. Thus AB = AC)
Thus, required area = ½ * 2√2 * 2√2 = 4 sq. units
Example 6: The line √3 Y = x is the radius of the circle. It meets the circle o=centered at origin O at point M (√3, 1). If PQ is the tangent to the circle at M as shown, find the length of the PQ.

a) (5/2)√3 units
b) 3 √3 units
c) 2√3 units
d) 8/√3 units
Ans: Option 'd' is correct
Sol: PQ is perpendicular to line Y = X / √3 (Since, radius of a circle is perpendicular to the tangent of the circle)
Therefore, slope of PQ = -1 / (1/ √3) = – √3 (Since, product of slopes of line perpendicular to each other is -1)
Therefore, Let equation of the line PQ be y = – √3x + c
Now at the point M, when x = √3, y = 1
Putting the above values of x and y in the above equation, we get c = 4 The equation of the line becomes, Y = – √3x + 4
Thus, by using the above equation, we get:
Coordinates of point P = (0, 4) and coordinates of point Q = (4/√3, 0) (Putting x = 0 in above equation, we find value of P and putting Y = 0 in above equation, we find value of Q)
Hence PQ = sqrt [(4/√3) 2 + 42] = 8/√3 units.
Example 7: What is the equation of a circle with centre of origin and radius is 6 cm?
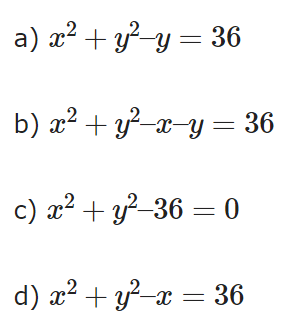
Ans: Option 'c' is correct
Sol: Given,
Center of the circle = (0,0)
Radius of the circle (r) = 6 cm∴ Equation of the circle is
Example 8: The equation of circle with centre (1, -2) and radius 4 cm is:
(a) x2 + y2 +2x - 4y = 11
(b) x2 + y2 + 2x - 4y = 16
(c) x2 + y2 - 2x + 4y = 16
(d) x2 + y2 - 2x + 4y = 11
Ans: Option 'd' is correct
Sol: Given,
Centre of the circle (a, b) = (1, -2)
Radius of the circle (r) = 4 cm
... Equation of the circle is (xa)2 + (y - b)2 = r2
=> (x-1)2 +(y-(-2))2 = 42
=> (x-1)2 + (y+2)2 = 42
=> x2+12 - 2.x.1 + y2 + 22 +2.y.2 = 16
=> x2 + 1 - 2x + y2 + 4 + 4y = 16
=> x2 - 2x + y2 + 4y = 16 - 1 - 4
=> x2 + y2 - 2x + 4y = 11
Hence, the correct answer is Option (d)
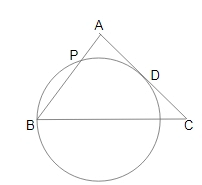
Example 9 3: In ΔABC, AB = AC. A circle drawn through B touches AC at D and intersect AB at P. If D is the mid point of AC and AP 2.5 cm, then AB is equal to:
(a) 9 cm
(b) 10 cm
(c) 7.5 cm
(d) 12.5 cm
Ans: Option 'b' is correct
Sol:
Given D is midpoint of AC so,AD = AC/2
But also given AC = AB
AD = AB/2 - (1)
AD is a tangent and APB is a secant. So the tangent secant theorem can be applied,
AD2 = AP X AB
(AB/4)2 = 2.5 × AB
AB2/4 = 2.5 × AB
AB = 10 cm
|
196 videos|131 docs|110 tests
|
FAQs on Important Formulas for CAT Coordinate Geometry
| 1. What are the basic coordinate geometry formulae that one should know for CAT preparation? |  |
| 2. How do you derive the equation of a line in slope-intercept form? |  |
| 3. What is the significance of the point-slope form of a line in coordinate geometry? |  |
| 4. Can you explain how to find the angle between two intersecting lines? |  |
| 5. What are some common mistakes to avoid when solving coordinate geometry problems in CAT? |  |

|
Explore Courses for CAT exam
|

|
 As it is mentioned in the question that the triangle is an isosceles triangle ,therefore the sides AB = BC = 6 units and the length of the third side = (62 + 62)1/2
As it is mentioned in the question that the triangle is an isosceles triangle ,therefore the sides AB = BC = 6 units and the length of the third side = (62 + 62)1/2