Coordinate Geometry Question with Answer | Quantitative Aptitude (Quant) - CAT PDF Download
Question 1: Set S contains points whose abscissa and ordinate are both natural numbers. Point P, an element in set S has the property that the sum of the distances from point P to the point (3,0) and the point (0,5) is the lowest among all elements in set S. What is the sum of abscissa and ordinate of point P?
A. 2
B. 3
C. 5
D. 4
Answer. 4
Explanation. Any point on the line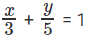 will have the shortest overall distance. However, we need to have integral coordinates. So, we need to find points with integral coordinates as close as possible to the line 5x + 3y = 15.
will have the shortest overall distance. However, we need to have integral coordinates. So, we need to find points with integral coordinates as close as possible to the line 5x + 3y = 15.
Substitute x =1, we get y = 2 or 3
Substitute x = 2, we get y = 1 or 2
Sum of distances for (1, 2) = √8 + √10
Sum of distances for (1, 3) = √13 + √5
Sum of distances for (2, 1) = √2 + √20
Sum of distances for (2, 2) = √5 + √13
√5 + √13 is the shortest distance.
Sum of abscissa + ordinate = 4
Hence, the answer is 4.
Choice D is the correct answer.
Question 2: Region R is defined as the region in the first quadrant satisfying the condition 3x + 4y < 12. Given that a point P with coordinates (r, s) lies within the region R, what is the probability that r > 2?
A. 1/4
B. 1/3
C. 1/5
D. 1/2
Answer. 1/4
Explanation.
Line 3x + 4y =12 cuts the x-axis at (4, 0) and y axis at (0, 3).
The region in the first quadrant satisfying the condition 3x + 4y < 12 forms a right triangle with sides 3, 4 and 5. Area of this triangle = 6 sq.units.
The lines x = 2 and 3x + 4y = 12 intersect at (2, 1.5). So, the region r > 2, 3x + 4y < 12 also forms a right triangle. This right triangle has base sides 2, 1.5.
Area of this triangle = 1.5
Probability of the point lying in said region = 1.5/6 = 1/4
Hence, the answer is 1/4
Choice A is the correct answer.
Question 3: Region Q is defined by the equation 2x + y < 40. How many points (r, s) exist such that r is a natural number and s is a multiple of r?
A. 84
B. 92
C. 105
D. 72
Answer. 92
Explanation.
When r = 1, s can take 37 values [37/1]
When r = 2, s can take 17 values [35/2]
When r = 3, s can take 11 values [33/3]
When r = 4, s can take 7 values [31/4]
When r = 5, s can take 5 values [29/5]
When r = 6, s can take 4 values [27/6]
When r = 7, s can take 3 values [25/7]
When r = 8, s can take 2 values [23/8]
When r = 9, s can take 2 values [21/9]
When r = 10, s can take 1 values [19/10]
When r = 11, 12, 13 s can take one value each.
Totally, there are 92 values possible.
Hence, the answer is 92.
Choice B is the correct answer.
Question 4: What is the equation of a set of points equidistant from the lines y = 5 and x = –4?
A. x + y = –1
B. x – y = –1
C. x + y = 1
D. –x + y = –1
Answer. x + y = 1
Explanation.
Let us try to draw the given lines on the coordinate plane.
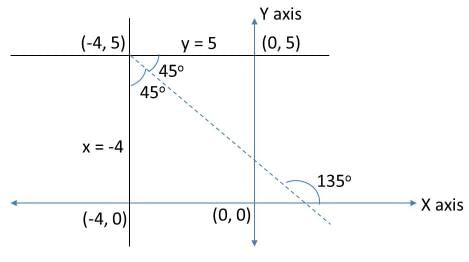
A set of points equidistant from the given two lines should lie on the dotted line as indicated. You can think of it as the perpendicular bisector to the base of an isosceles triangle formed by (–4, 5) and the two points on x = –4 and y = 5.
Or, the set of points equidistant from two lines form the angle bisector of the angle formed at the point of intersection of the two lines. The angle between these two lines is 90°. Importantly, the lines are parallel to the axes. So, thinking of the line that is the angle bisector of this angle should not be too difficult.
This dotted line is at an angle of 135o with respect to the positive direction of x–axis and also passes through (–4, 5).
Slope = m = tan (135o) = –1.
Therefore, the equation is given by (y – y1) = m
(x – x1) where (x1, y1) is (–4, 5).
(y – 5) = –(x + 4)
x + y = 1
Hence, the answer is x + y = 1.
Choice C is the correct answer.
Question 5: What is the area enclosed in the region defined by y = |x – 1| + 2, line x = 1, X–axis and Y–axis?
A. 5 sq units
B. 2.5 sq units
C. 10 sq units
D. 7 sq units
Answer. 2.5 sq units
Explanation.
Let us first draw y = |x|.
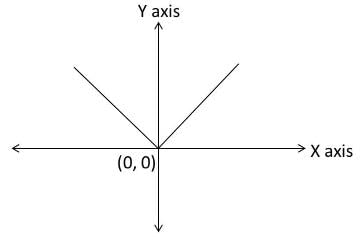
Now, y = |x – 1| is just a shift of ‘1’ unit to the right along the x–axis.
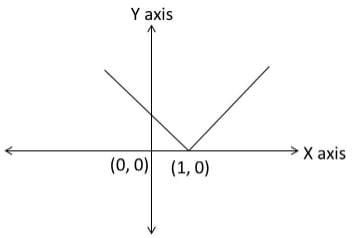
Now, y = |x – 1| + 2 is a shift of ‘2’ units to the top along the y–axis.
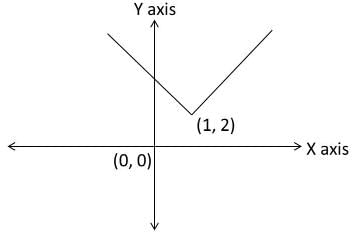
Now, let us complete the diagram by drawing the line x = 1 also.
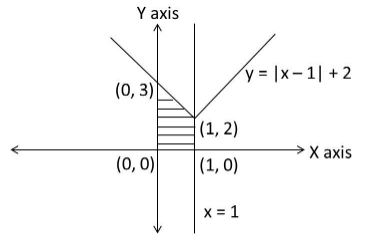
The required area is essentially the area of the shaded region.
The point of intersection of y = |x – 1| + 2 where the y–axis can be found by substituting x = 0 in the equation.
Thus we get y = 3.
Required area = Area of the trapezium formed by the points (0, 0), (1, 0), (1, 2) and (0, 3).
Area of a trapezium =  sum of the parallel sides
sum of the parallel sides 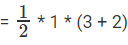 = 5/2 sq units.
= 5/2 sq units.
Hence, the answer is 2.5 sq units
Choice B is the correct answer.
Question 6: Find the area of the region that comprises all points that satisfy the two conditions x2 + y2 + 6x + 8y ≤ 0 and 4x ≥ 3y?
A. 25
B. 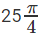
C. 
D. None of these
Answer. 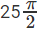 Explanation.
Explanation.
x2 + y2 + 6x + 8y < 0
x2 + 6x + 9 – 9 + y2 + 8y + 16 – 16 < 0
(x + 3)2 + (y + 4)2 < 25
This represents a circular region with centre (–3, –4) and radius 5 units. Substituting x = y = 0, we also see that the inequation is satisfied. This means that the circle also passes through the origin. To find out the intercepts that the circle cuts off with the axes, substitute x = 0 to find out the y–intercept and y = 0 to find out x–intercept. Thus x–intercept = –6 and y–intercept = –8.
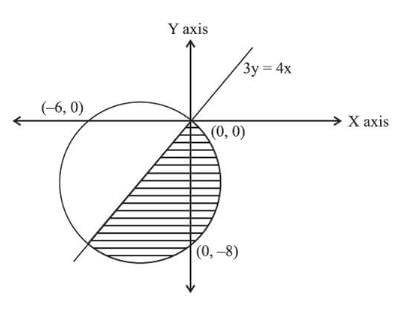
Now, the line 4x = 3y passes through the point (–3, –4). Or this line is the diameter of the circle. The area we are looking for is the area of a semicircle.
Required area 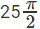
Hence, the answer is 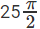 sq units
sq units
Choice C is the correct answer.
Question 7: What is the reflection of the point (4 , -3) in the line y = 1?
A. (4, -5)
B. (4, 5)
C. (-4, -5)
D. (-4, 5)
Answer. (4, 5)
Explanation.
Reflection of point (x , y) in line y = a is (x,-y+2a)
Now, Reflection of point (4,-3) in line y=1
= [4,3+2(1)]=(4,5)
⇒ Ans –> (B)
Question 8: At what point does the line 3x + 2y = -12 intercept the Y-axis?
A. (0,6)
B. (0,-6)
C. (-4,0)
D. (4,0)
Answer.
Explanation. (0,-6)
The line 3x + 2y = -12 will intercept the y-axis at x = 0
Thus, substituting value of x in above equation
⇒ 3(0) + 2y = -12
⇒ y = -12/2 = -6
Thus, the line will intercept y axis at (0,-6)
⇒ Ans – > (B)
Question 9: The area of triangle with vertices (5x,2x), (7x, 0) and (5x, 0) is 72 sq units. If x is a positive integer, what is the value of x?
A. 6
B. 3
C. 9
D. 12
E. 15
Answer. 6
Explanation.
The diagram with the given vertices is given below: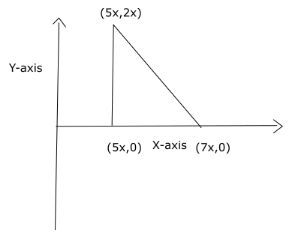
ABC is a right angled triangle with AB = BC = 2x and right angles at ∠ABC
Thus, area of the triangle = 1/2 * AB * BC = 1/2 * 2x * 2x = 2x2
2x2 = 72
x2 = 36
⇒ x = ± 6
Since x is positive, x = 6
Question 10: Find the intercepts made by the line 7x + 6y – 42 = 0 on y and x axis respectively.
A. (6,7)
B. (3,2)
C. (2,3)
D. (7,6)
Answer.
Explanation. (7,6)
The point where this line cuts the x axis, y coordinate will be 0 and the point where it cuts the y axis, x coordinate would be 0.
So y intercept = 7*0 + 6y = 42 => y = 7
Similarly x intercept = 7x + 6*0 = 42 => x = 6
Since the question asks the intercepts in the order y and x respectively, the correct answer is (7, 6)
Thus option D is the correct answer.
|
174 videos|243 docs|95 tests
|
FAQs on Coordinate Geometry Question with Answer - Quantitative Aptitude (Quant) - CAT
| 1. কো-অধিকার জ্যামিতি কী? |  |
| 2. কো-অধিকার কোন উদাহরণ দিতে পারে? |  |
| 3. কো-অধিকার এবং দুইটি বিন্দুর সম্পর্ক কী? |  |
| 4. কো-অধিকার কিভাবে ব্যবহার করা যায় গণিতে? |  |
| 5. কো-অধিকারের মৌলিক গণিত সূত্র কী? |  |
















