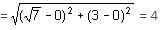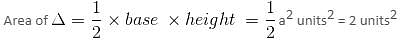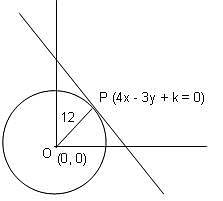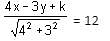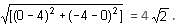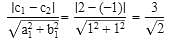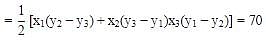This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Coordinate Geometry (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Coordinate Geometry
Try yourself:Radius of the circle passing through the foci of the ellipse x2/16 + y2/9 = 1 and having its centre at (0, 3) is
Explanation
For the given ellipse a2 = 16 and b2 = 9
⇒ a2(1 - e2) = 9
⇒ 16 - a2e2 = 9
⇒ ae = √7
So, foci are at (- √7, 0) and (√7, 0).
Hence, required length of radius

Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
Try yourself:If D (2, 1), E (-1, -2) and F (3, 3) are the mid-points of the sides BC, CA and AB, respectively, of the triangle ABC, then the equation of AB is
Explanation
As the slope of AB is equal to the slope of DE, i.e. 1, so the equation of line AB is x = y ⇒ x - y = 0.
Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
Try yourself:ABC is an isosceles triangle. If the coordinates of the ends of the base are B (1, 3) and C (-2, 7), then the coordinates of vertex A are
Explanation
The vertex A (x, y) is equidistant from B and C because ABC is an isosceles triangle.
Therefore, (x - 1)2 + (y - 3)2 = (x + 2)2 + (y - 7)2
⇒ 6x - 8y + 43 = 0
Now, from the options, we have
x = 5/6 and y = 6, which satisfy the above equation.
Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
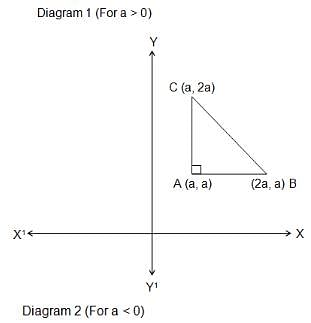
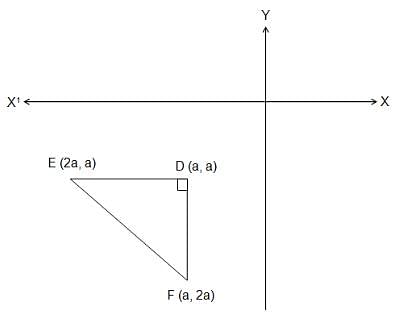
Try yourself:If the points (2a, a), (a, 2a) and (a, a) enclose a triangle of area 2 sq. units, then the value of a is
Explanation
Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
Try yourself:In which of the following equations are x and y intercepts not consecutive numbers?
Explanation
Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
Try yourself:If 4x - 3y + k = 0 represents a tangent to the circle x2 + y2 = 144, then what is the value of k?
Explanation

The perpendicular distance OP is given by the formula:

Also, (x, y) = (0, 0)
⇒ k = ± 60
Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
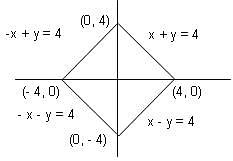
Try yourself:Find the area enclosed by |x| + |y| = 4.
Explanation

The four possible lines are:
x + y = 4; x - y = 4; - x - y = 4 and -x + y = 4
The four lines can be represented on the coordinate axes as shown in the figure.
Thus, a square is formed with the vertices as shown.
The side of the square is

The area of the square is (4√2)2 = 32 sq. units.
Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
Try yourself:What is the equation of the line parallel to the line x + 3y = -7 and passing through the centroid of the triangle formed by the intersection of the lines 3x - 4y = -11, 3x - y = -5 and 3x + 2y = 19?
Explanation
Slope of the line x + 3y = -7 is -1/3.
On solving the equation for the three lines, we get the vertices of the triangles as (-1, 2), (3, 5) and (1, 8).
So, the centroid of the triangle is ([-1 + 3 + 1] / 3, [2 + 5 + 8] / 3) or (1, 5)
Using the slope-point form of the equation of a line, we get the required equation: y - 5 = (-1/3)(x - 1), i.e. x + 3y = 16.
Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
Try yourself:Two sides of a square lie on the lines x + y = 1 and x + y + 2 = 0. What is its area ?
Explanation
The equations of parallel sides of the square are x + y − 1 = 0 and x + y + 2 = 0.
Therefore, Length of the side of the square = Distance between parallel side =

Hence, area of the square = (side)2 = 9/2 sq.units
Report a problem
Question for Practice Questions Level 3: Coordinate Geometry
Try yourself:The area of triangle formed by the points (p, 2 − 2p),(1 − p, 2p) and (−4 −p, 6 − 2p) is 70 sq. units. How many integral values of p are possible ?
Explanation
Given the points of triangle, A(p, 2 − 2p),B(1 − p, 2p) and C(−4 − p ,6 − 2p)
Area = 70sq.unit

{p[2p−6+2p]+(1−p)[6−2p+2p]+(−4−p)[2−2p−2p]}=140
p(4p−6)+(1−p)(4)−[(4+p)(2−4p)] =140
4p2 −6p+4−4p−[8−16p+2p−4p2] =140
4p2 −6p+4−4p−8+16p−2p+4p2 =140
8p2 +4p−144=0
2p2 +p−36=0
2p2 +9p−8p−36=0
p(2p+9)−4(2p+9)=0
(2p+9)=0,(p−4)=0
p = −9/2,p = 4
∴ Only one integral value is possible.
Report a problem