Couette Flow - 3 | Fluid Mechanics for Mechanical Engineering PDF Download
Flow between Two Concentric Rotating Cylinders
- Another example which leads to an exact solution of Navier-Stokes equation is the flow between two concentric rotating cylinders.
- Consider flow in the annulus of two cylinders (Fig. 26.5), where r1 and r2 are the radii of inner and outer cylinders, respectively, and the cylinders move with different rotational speeds ω1 and ω2 respectively

- From the physics of the problem we know, ,

- From the continuity Eq. and these two conditions, we obtain

which means vθ is not a function of θ. Assume z dimension to be large enough so that end effects can be neglected and  (any property) = 0.
(any property) = 0.
- This implies vθ = vθ (y) . With these simplifications and assuming that " θ symmetry" holds good, Navier-Stokes equation reduces to
 (26.17)
(26.17)
 (26.18)
(26.18)
- Equation (26.17) signifies that the centrifugal force is supplied by the radial pressure, exerted by the wall of the enclosure on the fluid. In other words, it describes the radial pressure distribution.
From Eq. (26.18), we get
 ( 26.19)
( 26.19)
For the azimuthal component of velocity, vθ, the boundary conditions are: at
 at
at  .
.- Application of these boundary conditions on Eq. (26.19) will produce

and 
- Finally, the velocity distribution is given by
 (26.20)
(26.20)
Calculation of Stress and Torque Transmitted
Now,  is the general stress-strain relation.
is the general stress-strain relation.

- In our case,
 (26.21)
(26.21)
- Equations (26.20) and (26.21) yields
 (26.22)
(26.22)
- Now,

and,

- For the case, when the inner cylinder is at rest and the outer cylinder rotates, the torque transmitted by the outer cylinder to the fluid is
 (26.23)
(26.23)
where l is the length of the cylinder.
- The moment T1, with which the fluid acts on the inner cylinder has the same magnitude. If the angular velocity of the external cylinder and the moment acting on the inner cylinder are measured, the coefficient of viscosity can be evaluated by making use of the Eq. (26.23).
|
56 videos|104 docs|75 tests
|
FAQs on Couette Flow - 3 - Fluid Mechanics for Mechanical Engineering
| 1. What is Couette flow? |  |
| 2. How is the velocity profile in Couette flow determined? |  |
| 3. What are the applications of Couette flow in mechanical engineering? |  |
| 4. What are the assumptions made in the analysis of Couette flow? |  |
| 5. How is the shear stress calculated in Couette flow? |  |
|
56 videos|104 docs|75 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|
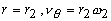 .
.
















