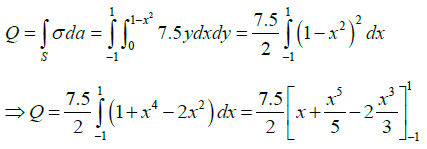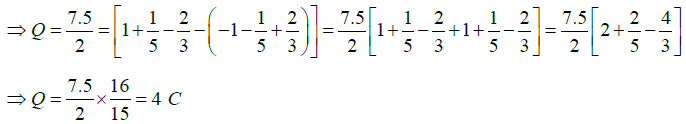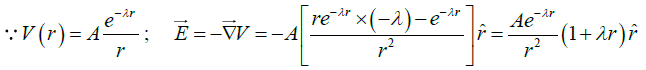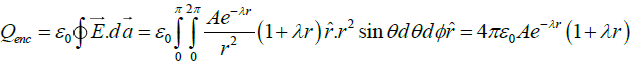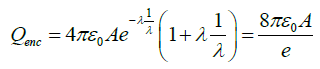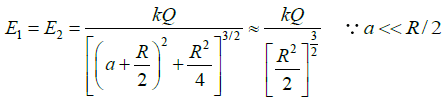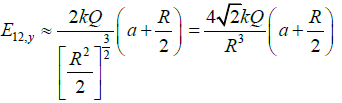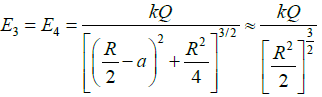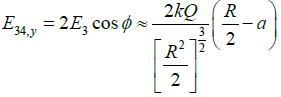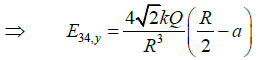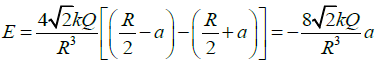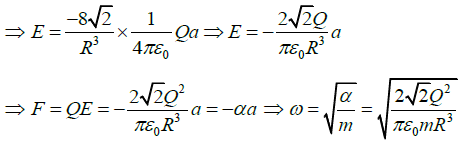Coulomb’s Law, Gauss Law and Electrostatic Potential: Assignment | Electricity & Magnetism - Physics PDF Download
Q.1. (a) A static charge distribution gives rise to an electric field of the form 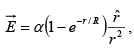 where α and R are positive constants. Find the charge contained within a sphere of radius R, centered at the origin.
where α and R are positive constants. Find the charge contained within a sphere of radius R, centered at the origin.
(b) An electric field 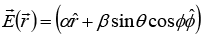 exists in space. What will be the total charge enclosed in a sphere of unit radius centered at the origin?
exists in space. What will be the total charge enclosed in a sphere of unit radius centered at the origin?
(a)
(b)
Q.2. A thin, nonconducting ring of radius R, as shown below, which has a charge Q uniformly spread out on it.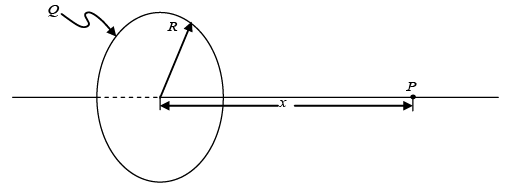 (a) At what distance x electric field, calculated directly above the center of the loop, is maximum.
(a) At what distance x electric field, calculated directly above the center of the loop, is maximum.
(b) Find the electric potential at a point P, which is located on the axis of symmetry a distance x from the center of the ring.
(c) A small particle of mass m and charge -q is placed at point P and released. If R>>x, the particle will undergo oscillations along the axis of symmetry then find its angular frequency.
(a)
For maximum E,
(b) The electric field at point P is
Recall the elementary equations,
(c)
Small oscillations have the same form as simple harmonic oscillations, i.e,
The angular frequency is
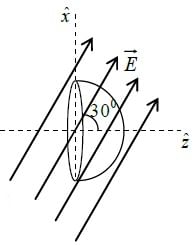
Q.3. A closed Gaussian surface consisting of a hemisphere and a circular disc of radius R, is placed in a uniform electric field 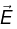 , as shown in the figure. The circular disc makes an angle θ = 30º with the vertical. Find the flux of the electric field vector coming out of the curved surface of the hemisphere.
, as shown in the figure. The circular disc makes an angle θ = 30º with the vertical. Find the flux of the electric field vector coming out of the curved surface of the hemisphere.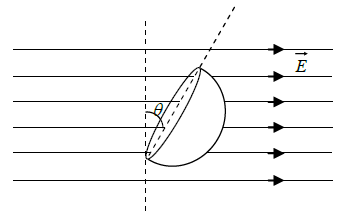
OR
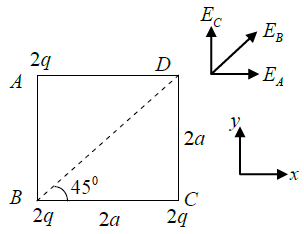
Q.4. Three charges, each equal to 2q, are placed at the three corners (A, B and C) of a square of side 2a. Find the magnitude and directions of electric field at the fourth corner D.
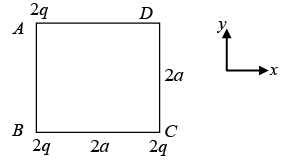
Electric field due to charge at A
Electric field due to charge at C,
Electric field due to charge at D,
Resultant along x-direction is
Resultant along x-direction is
Thus magnitude of resultant field isand direction along field EB .
Q.5. (a) For an infinitely long wire with uniform line-charge density, λ along the z -axis, find the electric field at a point ( a, b, 0 ) away from the origin.
(b) A uniform line charge, infinite in extent, having charge per unit length 10 nC/m lies along the z -axis. Find the magnitude of electric field 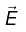 at ( 6, 8, 3) m.
at ( 6, 8, 3) m.
(a)
(b)
Q.6. A solid sphere of radius R has a charge density, given by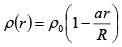
where r is the radial coordinate and ρ0 , a and R are positive constants.
(a) Find the magnitude of the electric field at r = R/2
(b) Find the magnitude of the electric field at r =R
(c) At what radial distance r, magnitude of the electric field is maximum. Also find the maximum electric field.
(d) If the magnitude of the electric field at r = R/2 is 1.25 times that at r = R , then find the value of a.
(a) The electric field at r
(b) The electric field at r
(c) For maximum electric field
Thus maximum value is
(d)
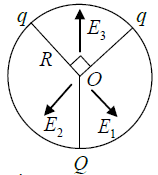
Q.7. Three charges are located on the circumference of a circle of radius R as shown in the figure below. The two charges q subtends an angle 90° at the centre of the circle. The charge Q is symmetrically placed with respect to the charges q.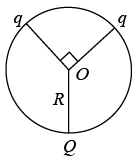 (a) If Q = q, then find the magnitude and direction of electric field at centre O.
(a) If Q = q, then find the magnitude and direction of electric field at centre O.
(b) If Q = 2q, then find the magnitude and direction of electric field at centre O.
(a)
If Q = q ;
Resultant of E1 and E2 is
∵ E12 > E3
Thus resultant field isin downward direction.
(b)
If Q = 2q ;
Resultant of E1 and E2 is
∵ E12 < E3Thus resultant field is
in upward direction
Q.8. Two large nonconducting sheets one with a fixed uniform positive charge and another with a fixed uniform negative charge are placed at a distance of 1 meter from each other. The magnitude of the surface charge densities are σ+ = 6.8μC/m2 for the positively charged sheet and σ- = 4.3μC/m2 for the negatively charged sheet.
(a) What is the electric field in the region between the sheets?
(b) What is the electric field in the region outside the sheets?
(a) Electric field between the sheet is(b) Electric field outside the sheet (towards right) is
Electric field outside the sheet (towards left) is
Q.9. In a coaxial cable, the radius of the inner conductor is 2mm and that of the outer one is 5 mm. The inner conductor is at a potential of 10V, while the outer conductor is grounded. Find the value of the potential at a distance of 3.5 mm from the axis.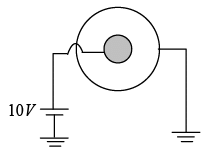
∵∇2V = 0
In Cylindrical coordinate system,
Thus 10 = Aln2+ B and 0 = Aln5 + B
⇒V(r = 3.5) = Aln3.5+ B = 3.8 V
Q.10. (a) The electrostatic potential V(x, y) in some region is given by V(x, y)=3x2-3y2. Find the charge density ρ. Find the x and y -component of the electric field at the origin.
(b) If the electrostatic potential V (r,θ,ϕ ) in a charge free region has the form V(r.θ.ϕ) = f(r) cosθ, then set up the second order differential equation in f(r).
(c) If the electrostatic potential in spherical polar coordinates is 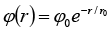 where φ0 and r0 are constants, then find the charge density at a distance r = r0.
where φ0 and r0 are constants, then find the charge density at a distance r = r0.
(a)
(b)
(c)
At a distance r = r0,
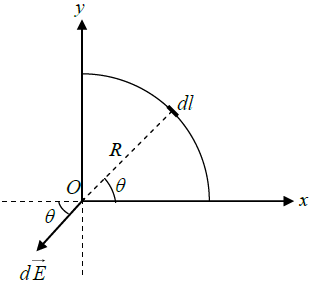
Q.11. A segment of a circular wire of radius R, extending from θ = 0 to π/2, carries a constant linear charge density λ . Find the electric field at origin O.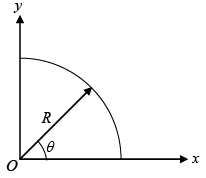
where
andSimilarly
Q.12. The plates of a parallel plate capacitor (which are normal to the x-axis) are located at x = 0 and x = 2a . The plate at x = 0 is grounded while the other plate is at a potential V0. The space between the plates has uniform volume charge density ρ.
(a) Find the potential V(x) between the plates.
(b) Find the electric field E(x) between the plates.
(a) The Laplace’s equation in Cartesian coordinates system is
as V is only function of x , we have the differential equation,
by integrating we have the solution of this equation as
where A and B are constants. The two equations need to be solved for the following boundary conditions:(i) x = 0 ;V = 0
(ii) x = 2a; V= V0
Substituting these boundary conditions, we get
At x = 0 , V(0) = 0 = 0 = 0 + B ⇒ B = 0
At x = 2a,(b)
Q.13. Consider a sphere S1 of radius R which carries a uniform charge of density ρ. A smaller sphere S2 of radius a<R/2 is cut out and removed from it. The centres of the two spheres are separated by the vector 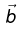 as shown in the figure. Find the electric field at a point P inside S2.
as shown in the figure. Find the electric field at a point P inside S2.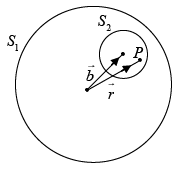
Electric field at P due to S1 is
Electric field at P due to 2 S (assume -ρ ) is
Thus
Q.14. The shape of a dielectric lamina is defined by the two curves y = 0 and y = 1-x2. If the charge density of the lamina is σ = 7.5yC/m2, then find the total charge on the lamina.
Total charge on the lamina is
Q.15. The electrostatic potential due to a charge distribution is given by 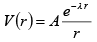 where A and λ are constants.
where A and λ are constants.
a) Find the electric field.
(b) Find the total charge enclosed within a sphere of radius 1/λ, with its origin at r = 0.
(a)
(b)
Thus total charge enclosed within a sphere of radius r = 1/λ is
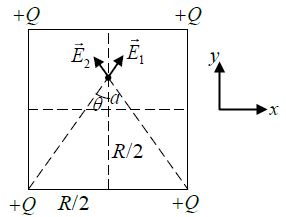
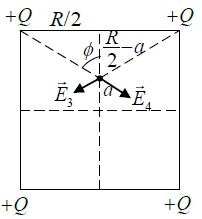
Q.16. Four equal charges of +Q each are kept at the vertices of a square of side R. A particle of mass m and charge +Q is placed in the plane of the square at a short distance a(<<R ) from the centre. If the motion of the particle is confined to the plane, it will undergo small oscillations then find its angular frequency.
Resultant field E12,y = 2E1 cos θSimilarly;
Resultant
Resultant
|
82 videos|32 docs|22 tests
|
FAQs on Coulomb’s Law, Gauss Law and Electrostatic Potential: Assignment - Electricity & Magnetism - Physics
| 1. What is Coulomb's law? |  |
| 2. What is Gauss's law? |  |
| 3. How is electrostatic potential defined? |  |
| 4. What is the relationship between electric potential and electric field? |  |
| 5. How does the electric potential vary around a point charge? |  |

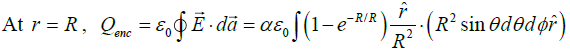
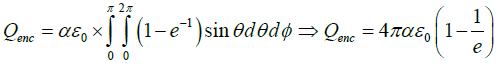
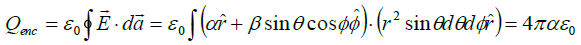
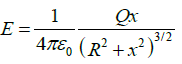
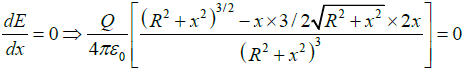
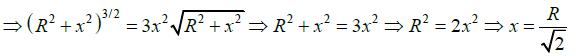
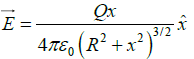
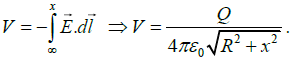
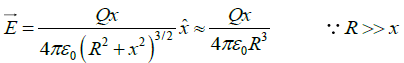
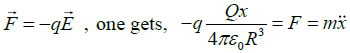
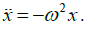
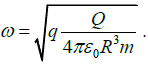
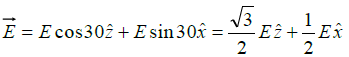
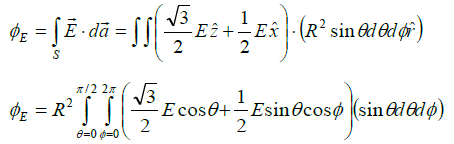
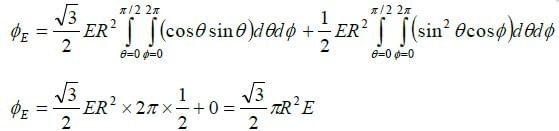
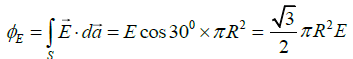
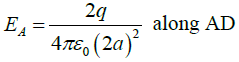
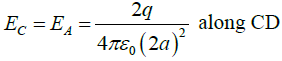
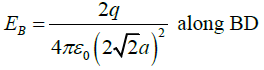
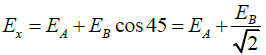
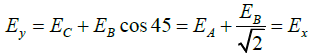
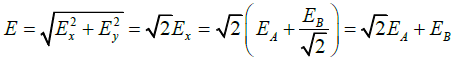
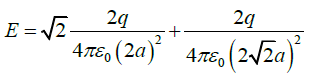
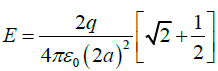 and direction along field EB .
and direction along field EB .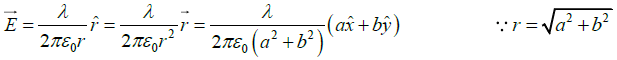
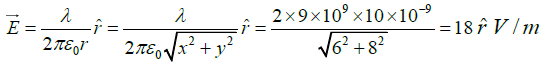
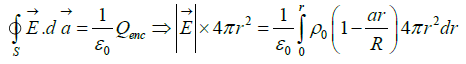
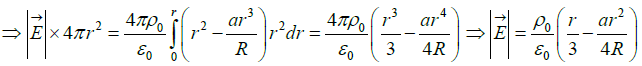

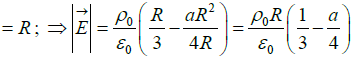
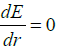
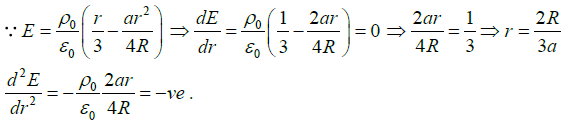
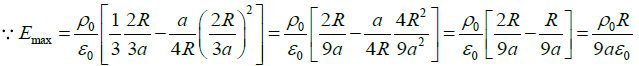
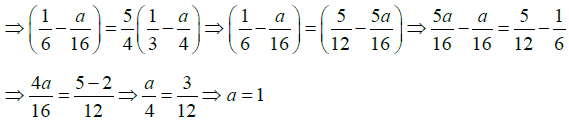
 If Q = q ;
If Q = q ;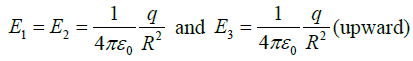
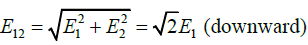
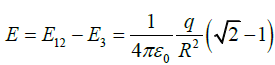 in downward direction.
in downward direction.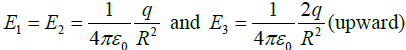
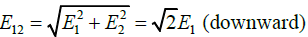
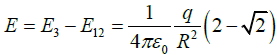 in upward direction
in upward direction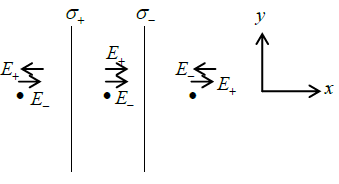
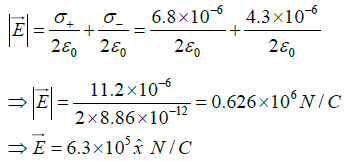
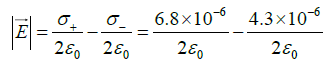
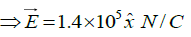
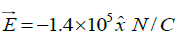

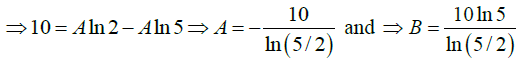

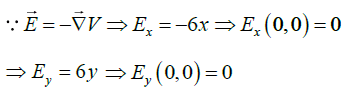
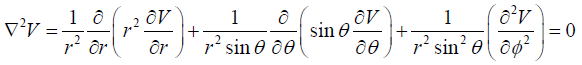
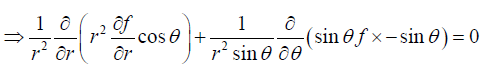
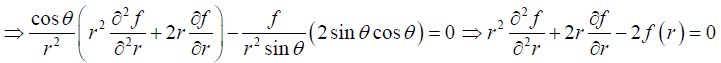
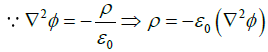
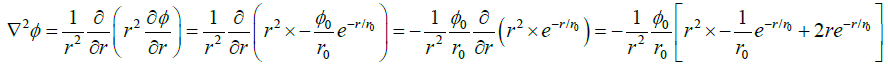
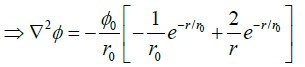
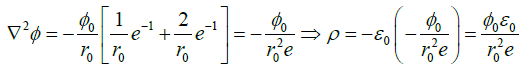
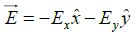
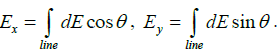
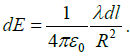
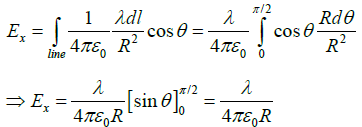
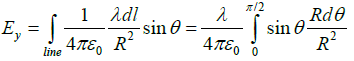
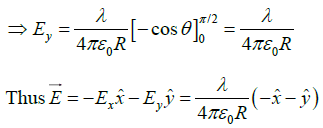
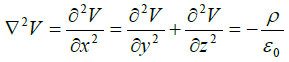 as V is only function of x , we have the differential equation,
as V is only function of x , we have the differential equation, 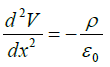 by integrating we have the solution of this equation as
by integrating we have the solution of this equation as 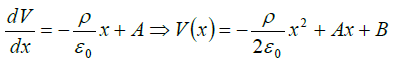 where A and B are constants. The two equations need to be solved for the following boundary conditions:(i) x = 0 ;V = 0
where A and B are constants. The two equations need to be solved for the following boundary conditions:(i) x = 0 ;V = 0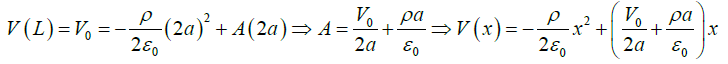 (b)
(b)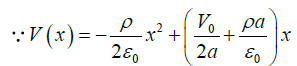
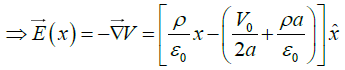
 Electric field at P due to S1 is
Electric field at P due to S1 is 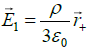
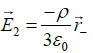
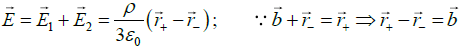
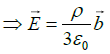
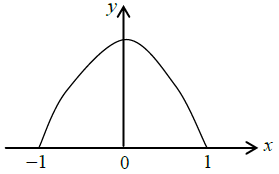 Total charge on the lamina is
Total charge on the lamina is