Coupled oscillators | Basic Physics for IIT JAM PDF Download
In the section on simple harmonic oscillators, the motion of a single particle held in place by springs was considered. In this section, the motion of a group of particles bound by springs to one another is discussed. The solutions of this seemingly academic problem have far-reaching implications in many fields of physics. For example, a system of particles held together by springs turns out to be a useful model of the behaviour of atoms mutually bound in a crystalline solid.
To begin with a simple case, consider two particles in a line, as shown in Figure 15. Each particle has mass m, each spring has spring constant k, and motion is restricted to the horizontal, or x, direction. Even this elementary system is capable of surprising behaviour, however. For instance, if one particle is held in place while the other is displaced, and then both are released, the displaced particle immediately begins to execute simple harmonic motion. This motion, by stretching the spring between the particles, starts to excite the second particle into motion. Gradually the energy of motion passes from the first particle to the second until a point is reached at which the first particle is at rest and only the second is oscillating. Then the process starts all over again, the energy passing in the opposite direction.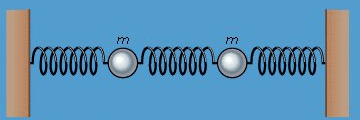
Figure 15: Coupled oscillators.
To analyze the possible motions of the system, one writes equations similar to equation (11), giving the acceleration of each particle owing to the forces acting on it. There is one equation for each particle (two equations in this case). The force on each particle depends not only on its displacement from its equilibrium position but also on its distance from the other particle, since the spring between them stretches or compresses according to that distance. For this reason the motions are coupled, the solution of each equation (the motion of each particle) depending on the solution of the other (the motion of the other).
Analyzing the system yields the fact that there are two special states of motion in which both particles are always in oscillation with the same frequency. In one state, the two particles oscillate in opposite directions with equal and opposite displacements from equilibrium at all times. In the other state, both particles move together, so that the spring between them is never stretched or compressed. The first of these motions has higher frequency than the second because the centre spring contributes an increase in the restoring force.
These two collective motions, at different, definite frequencies, are known as the normal modes of the system.
If a third particle is inserted into the system together with another spring, there will be three equations to solve, and the result will be three normal modes. A large number N of particles in a line will have N normal modes. Each normal mode has a definite frequency at which all the particles oscillate. In the highest frequency mode each particle moves in the direction opposite to both of its neighbours. In the lowest frequency mode, neighbours move almost together, barely disturbing the springs between them. Starting from one end, the amplitude of the motion gradually builds up, each particle moving a bit more than the one before, reaching a maximum at the centre, and then decreasing again. A plot of the amplitudes, shown in Figure 16, basically describes one-half of a sine wave from one end of the system to the other. The next mode is a full sine wave, then 3/2 of a sine wave, and so on to the highest frequency mode, which may be visualized as N/2 sine waves. If the vibrations were up and down rather than side to side, these modes would be identical to the fundamental and harmonic vibrations excited by plucking a guitar string.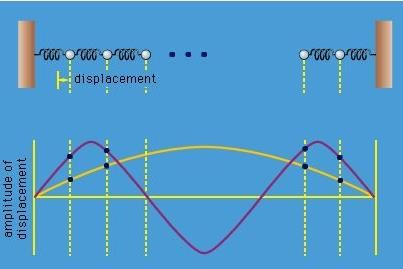
Figure 16: Normal modes.
The atoms of a crystal are held in place by mutual forces of interaction that oppose any disturbance from equilibrium positions, just as the spring forces in the example above. For small displacements of the atoms, they behave mathematically just like spring forces—i.e., they obey Hooke’s law, equation 10. Each atom is free to move in three dimensions rather than one, however; therefore each atom added to a crystal adds three normal modes. In a typical crystal at ordinary temperature, all these modes are always excited by random thermal energy. The lower-frequency, longer-wavelength modes may also be excited mechanically. These are called sound waves.
|
217 videos|156 docs|94 tests
|
FAQs on Coupled oscillators - Basic Physics for IIT JAM
| 1. What are coupled oscillators in physics? |  |
| 2. How do coupled oscillators behave when they are in phase? |  |
| 3. Can coupled oscillators exhibit anti-phase behavior? |  |
| 4. How does the coupling strength affect the behavior of coupled oscillators? |  |
| 5. What are some real-world examples of coupled oscillators? |  |





















