Cube and Cuboid | Mathematics for Digital SAT PDF Download

Introduction

Cube and cuboid are three-dimensional shapes that consist of six faces, eight vertices and twelve edges. The primary difference between them is a cube has all its sides equal whereas the length, width and height of a cuboid are different. Both shapes look almost the same but have different properties. The area and volume of cube, cuboid and also cylinder differ from each other.
In everyday life, we have seen many objects like a wooden box, a matchbox, a tea packet, a chalk box, a dice, a book, etc. All these objects have a similar shape. All these objects are made of six rectangular planes or square planes. In mathematics, the shape of these objects is either a cuboid or a cube. Here, in this article, we will learn the difference between cube and cuboid shapes with the help of their properties and formulas of surface area and volume.

Definition of Cube and Cuboid Shape

The cube and cuboid shapes in Maths are three-dimensional shapes. The cube and cuboid are obtained by giving a thickness to the 2D square and rectangle respectively.

• Cube: A cube is a three-dimensional shape that is defined in the XYZ plane. It has six faces, eight vertices and twelve edges. All the faces of the cube are square in shape and have equal dimensions.
• Cuboid: A cuboid is also a polyhedron having six faces, eight vertices and twelve edges. The faces of the cuboid are parallel. But not all the faces of a cuboid are equal in dimensions.

Hence, cube and cuboid shapes have six faces, eight vertices and twelve edges.

Difference Between Cube and Cuboid

The difference between the cube and cuboid shapes are as follows:

• The sides of the cube are equal but for cuboids they are different.
• The sides of the cube are square, but for the cuboids they are in rectangular shape.
• All the diagonals of the cube are equal but a cuboid has equal diagonals for only parallel sides.

Cube and Cuboid Shape

As we already know, both cube and cuboid are in 3D shape, whose axes go along the x-axis, y-axis and z-axis. Now, let us learn in detail.
A cuboid is a closed 3-dimensional geometrical figure bounded by six rectangular plane regions.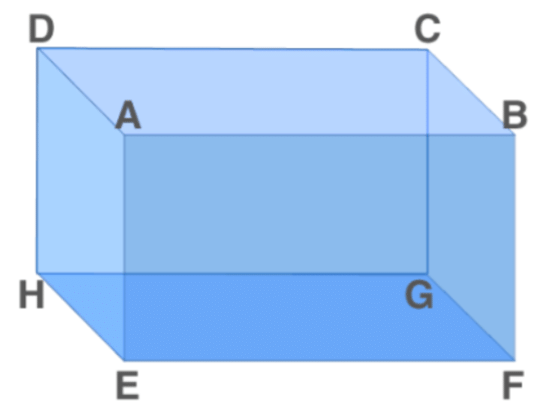
Cuboid Shape

Properties of a Cuboid

Below are the properties of the cuboid, its faces, base and lateral faces, edges and vertices.

Faces of Cuboid

• A Cuboid is made up of six rectangles, each of the rectangles is called the face. In the figure above, ABFE, DAEH, DCGH, CBFG, ABCD and EFGH are the 6 faces of the cuboid.
• The top face ABCD and the bottom face EFGH form a pair of opposite faces. Similarly, ABFE, DCGH, and DAEH, CBFG are pairs of opposite faces. Any two faces other than the opposite faces are called adjacent faces.
• Consider a face ABCD, the adjacent face to this are ABFE, BCGF, CDHG, and ADHE.

Base and lateral faces

• Any face of a cuboid may be called the base of the cuboid. The four faces which are adjacent to the base are called the lateral faces of the cuboid. Usually, the surface on which a solid rests is known to be the base of the solid.
• In Figure (1) above, EFGH represents the base of a cuboid.

Edges

• The edge of the cuboid is a line segment between any two adjacent vertices. 
• There are 12 edges, they are AB, AD, AE, HD, HE, HG, GF, GC, FE, FB, EF and CD and the opposite sides of a rectangle are equal. 
• Hence, AB = CD = GH = EF, AE = DH = BF = CG and EH = FG = AD = BC. 

Vertices of Cuboid

• The point of intersection of the 3 edges of a cuboid is called the vertex of a cuboid. 
• A cuboid has 8 vertices. A, B, C, D, E, F, G and H represent vertices of the cuboid in fig 1. 
• By observation, the twelve edges of a cuboid can be grouped into three groups, such that all edges in one group are equal in length, so there are three distinct groups and the groups are named as length, breadth and height.
• A solid having its length, breadth, and height all to be equal in measurement is called a cube. A cube is a solid bounded by six square plane regions, where the side of the cube is called the edge.

Properties of Cube

• A cube has six faces and twelve edges of equal length.
• It has square-shaped faces.
• The angles of the cube in the plane are at a right angle.
• Each face of the cube meets four other faces.
• Each vertex of the cube meets three faces and three edges.
• The opposite edges of the cube are parallel to each other.

Cube and Cuboid Formulas

The formulas for cube and cuboid shapes are defined based on their surface areas, lateral surface areas and volume.

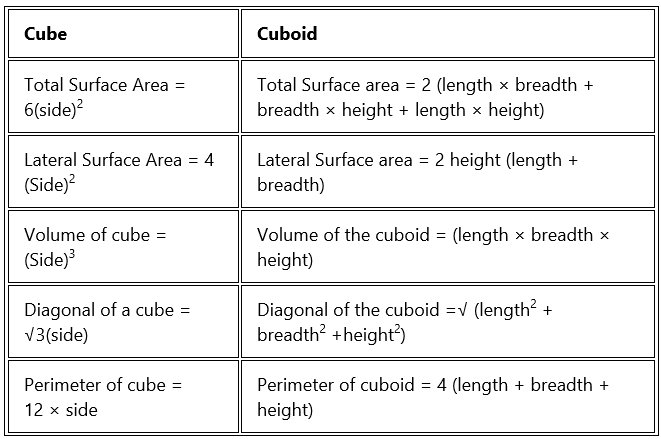
Surface Area of Cube and Cuboid

The surface area of a cuboid is equal to the sum of the areas of its six rectangular faces.
Cube and Cuboid Formula

Consider a cuboid having the length to be ‘l’ cm, breadth be ‘b’ cm and height be ‘h’ cm.

• Area of face EFGH = Area of Face ABCD = (l × b) cm²
• Area of face BFGC = Area of face AEHD = (b × h) cm²
• Area of face DHGC = Area of face ABFE = (l × h) cm²

Total surface area of a cuboid = Sum of the areas of all its 6 rectangular faces

Total Surface Area of Cuboid= 2(lb + bh + lh)

Example: If the length, breadth and height of a cuboid are 5 cm, 3 cm and 4 cm, then find its total surface area.

Given, Length, l = 5 cm, Breadth, b = 3 cm and Height, h = 4 cm.
Total surface area (TSA) = 2(lb + bh + lh)
= 2(5 × 3 + 3 × 4 + 5 × 4)
= 2(15 + 12 + 20)
= 2(47)
= 94 sq.cm.

Lateral surface area of a Cuboid

The sum of surface areas of all faces except the top and bottom face of a solid is defined as the lateral surface area of a solid.
Consider a Cuboid of length, breadth and height to be l, b and h respectively.
Lateral surface area of the cuboid= Area of face ADHE + Area of face BCGF + Area of face ABFE + Area of face DCGH
=2(b × h) + 2(l × h)
=2h(l + b)
LSA of Cuboid = 2h(l +b)

Example: If the length, breadth and height of a cuboid are 5 cm, 3 cm and 4 cm, then find its lateral surface area.

Given, Length = 5 cm, Breadth = 3 cm and Height = 4 cm
LSA = 2h(l + b)
LSA = 2 × 4(5 + 3)
LSA = 2 × 4(8)
LSA = 2 × 32 = 64 cm²

Surface Area of a Cube

For cube, length = breadth = height
Suppose the length of an edge = l
Hence, surface area of the cube = 2(l × l +l × l + l × l) = 2 x 3l²  = 6l²
Total Surface Area of Cube= 6l²
Example: If the length of the side of the cube is 6 cm, then find its total surface area.

Given, side length = 6 cm

TSA of cube = 6l² 
TSA = 6 (6)² 
TSA = 6 × 36 
TSA = 216 sq.cm 

Lateral surface area of a Cube

Formula to find the Lateral surface area of the cube is: 2(l × l + l × l) = 4l²

LSA of Cube = 4l²

Example: If the length of the side of the cube is 6 cm, then find its lateral surface area.

Given,

Side length, l = 6 cm
LSA of cube = 4l² 
LSA = 4 (6)²
LSA = 4 x 36 = 144 sq.cm

Volume of the Cube and Cuboid

Volume of Cuboid:
The volume of the cuboid is equal to the product of the area of one surface and height.
Volume of the cuboid = (length × breadth × height) cubic units

Volume of the cuboid = ( l × b × h) cubic units

Example: If the length, breadth and height of a cuboid are 5 cm, 3 cm and 4 cm, then find its volume.

Given, Length (l) = 5 cm, Breadth (b) = 3 cm and Height (h) = 4 cm
Volume of cuboid = l × b × h
V = 5 × 3 × 4
V = 60 cubic cm

Volume of the Cube:
The volume of the cube is equal to the product of the area of the base of a cube and its height. As we know already, all the edges of the cube are of the same length. Hence,
Volume of the cube = l² × h 
Since, l = h 
Therefore,
Volume of the cube = l² × l
Volume of the cube = l³ cubic units

Example: If the length of the side of the cube is 6 cm, then find its volume.

Given, side length = 6 cm
Volume of cube = side³
V = 6³
V = 216 cubic cm

Diagonal of Cube and Cuboid
The length of diagonal of the cuboid is given by:
Diagonal of the cuboid =√( l² + b² +h²)
The length of diagonal of a cube is given by:
Diagonal of a cube = √3l
Perimeter of Cube and Cuboid
The perimeter of the cuboid is based on its length, width and height. Since the cuboid has 12 edges and the value of its edges are different from each other, therefore, the perimeter is given by:
Perimeter of a cuboid =  4 (l + b + h)
where l is the length
b is the breadth
h is the height

Example: If the length, width and height of a cuboid are 5 cm, 3 cm and 4 cm, find its Perimeter.

Given, Length = 5 cm, Width = 3 cm and Height = 4 cm
Perimeter = 4 (l + b + h) = 4 (5 + 3 + 4)
P = 4 (12)
P = 48 cm

The perimeter of the cube also depends upon the number of edges it has and the length of the edges. Since the cube has 12 edges and all the edges have equal length, the perimeter of the cube is given by:
Perimeter of a cube =  12l
where l is the length of the edge of the cube

Example: If the side length of the cube is 6 cm, then find its perimeter.

Given , l = 6 cm
The perimeter of cube = 12l 
P = 12 × 6
P = 72 cm