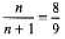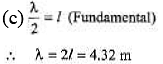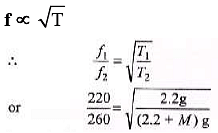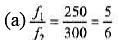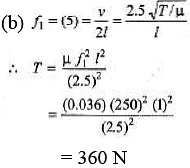DC Pandey Solutions: Superposition of Waves - 1 - Airforce X Y / Indian Navy SSR PDF Download
Introductory Exercise 15.1
Q.1. A string vibrates according to the equation 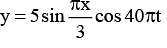 where x and y are in centimetres and t is in seconds.
where x and y are in centimetres and t is in seconds.
(a) What is the speed of the component wave?
(b) What is the distance between the adjacent nodes?
(c) What is the velocity of the particle of the string at the position x = 1.5 cm when t = 9/8 s?
Sol.
(b) Distance between adjacent nodes
Now substitute the given values of x and t.
Q.2. If two waves differ only in amplitude and are propagated in opposite directions through a medium, will they produce standing waves? Is energy transported?
Sol. In this case, node points will also oscillate, but standing waves are formed.
Ques 3: Figure shows different standing wave patterns on a string of linear mass density 4.0 × 10-2 kg/m under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0 m.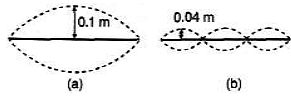
(i) Obtain the frequencies of the modes shown in figures (a) and (b).
(ii) Write down the transverse displacement y as a function of x and f for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).
Sol:
Q.4. A 160 g rope 4 m long is fixed at one end and tied to a light string of the same length at the other end. Its tension is 400 N.
(a) What are the wavelengths of the fundamental and the first two overtones?
(b) What are the frequencies of these standing waves?
[Hint: In this case, the fixed end is a node and the end tied with the light string is antinode.]
Sol.
(a) 1 = λ1/4
Now
Similarly f2 and f3.
Q.5. A string fastened at both ends has successive resonances with wavelengths of 0.54m for the nth harmonic and 0.48 m for the (n +1)th harmonic.
(a) Which harmonics are these?
(b) What is the length of the string?
(c) What is the wavelength of the fundamental frequency?
Sol.
or...(i)
Similarly,
or... (ii)
From Eqs. (i) and (ii) we have,
(b) From Eq. (i)
l = (0.27)n = 0.27 × 8 = 2.16 m
Q.6. If the frequencies of the second and fifth harmonics of a string differ by 54 Hz. What is the fundamental frequency of the string?
Sol.
5f - 2f=54
3f = 54 f = 18 Hz
Q.7. A wire is attached to a pan of mass 200 g that contains a 2.0 kg mass, as shown in the figure. When clucked, the wire vibrates at a fundamental frequency of 220 Hz. An additional unknown mass M is then added to the pan and a fundamental frequency of 260 Hz is detected. What is the value of M1

Sol.
Solving we get,
M = 0.873 kg
Q.8. A wire fixed at both ends is 1.0 m long and has a mass of 36 g. One of its oscillation frequencies is 250 Hz and the next higher one is 300 Hz.
(a) Which harmonics do these frequencies represent?
(b) What is the tension in the wire?
Sol.
So, f1 is 5th harmo nic and f2 is 6th harmonic.
FAQs on DC Pandey Solutions: Superposition of Waves - 1 - Airforce X Y / Indian Navy SSR
| 1. What is the concept of superposition of waves? |  |
| 2. How can superposition of waves be used to analyze interference patterns? |  |
| 3. What is the principle of superposition and how does it apply to wave interference? |  |
| 4. Can waves of different frequencies superpose and interfere with each other? |  |
| 5. How does the superposition of waves relate to the phenomenon of diffraction? |  |

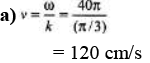
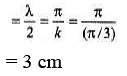

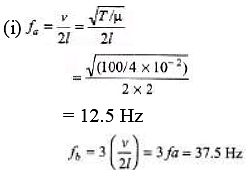

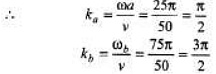

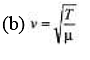

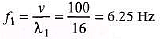
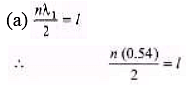
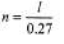 ...(i)
...(i)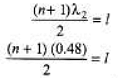
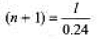 ... (ii)
... (ii)