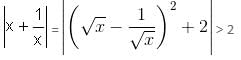This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Exponents & Logarithm (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:What is the value of x + y in the following two equations?
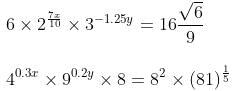
Explanation
The given equations in the simplest form can be written as:
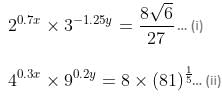
From equation (ii),
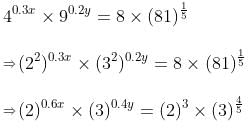
⇒ 0.6x = 3
⇒ x = 5
And 0.4y = 4/5
⇒ y = 2
So, the sum of the values of x and y is given as 7.
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:1 + loge z + 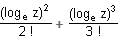 + ... is equal to
+ ... is equal to
Explanation
We know that
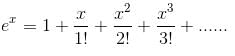
Put x = loge(z)
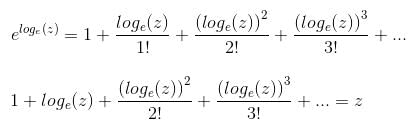
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:The population of microbial bacteria "Gram staminee" increases exponentially as P(t) = aebt. The population of bacteria at the beginning of experiment at 10 a.m. was 20, which grows up to 40 by 12 p.m. What will be the population of bacteria at 3 p.m.?
Explanation
Initially at 10 a.m., i.e. at t = 0, population of the bacteria was 20.
At 12 p.m., t = 2 and at 3 p.m., t = 5
Now, P(0) = aeb(0) = ae0 = a = 20 (given)
Now, at t = 2, P(t) = 40
⇒ 40 = 20eb(2)
⇒ e2b = 2
Taking log of both sides, we get
2b = loge 2 (log e = 1)
2b = 0.693
b = 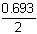 = 0.346
= 0.346
∴ P(t) = 20e0.346t
∴ P(5) = 20e0.346 x 5
= 20 x 5.64
= 112.8
Hence, population of bacteria at 3 p.m. = 113
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:If 10x = x50, find the value of x.
Explanation
10x = x50
Take log of both L.H.S. and R.H.S.
L.H.S. = log (10x) = x (log 10) = x (because log 10 = 1)
R.H.S = log (x50) = 50 log x
L.H.S. = R.H.S.
x = 50 log x
Case I:
If x = 1, then
1 = 50 (log 1) (because log 1 = 0)
1 = 0 (Not possible)
Case II:
If x = 10, then
10 = 50 log (10)
10 = 50 (Not possible) (because log 10 = 1)
Case III:
If x = √10, then
√10= 50 log (√10)
√10 = 25 (Not possible) (because log √10 = 1/2)
Case IV:
If x = √10, then
√10 = 50 log (100) = 50 log [(10)2]
= 50 × 2 log (10) (because log a = x log a)
= 50 × 2 × 1 (because log 10 = 1)
100 = 100
L.H.S. = R.H.S.
Hence, x = 100
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:If P = log23 and Q = log69, which of the following options is true?
Explanation
log22 < log23 < log24
i.e. 1 < P < 2
Similarly, log66 < log69 < log636
1 < Q < 2
Both P and Q belong to the interval (1, 2).
We shall now compare both P and Q with the average of 1 and 2, i.e. 3/2.
Let us assume that log2 3 > 3/2
Then 3 > 23/2 ⇒ 32 > 23
i.e. 9 > 8. This is true
P > 3/2 is correct.
We shall also suppose that log6 9 > 3/2
i.e. 9 > 63/2
92 > 63
i.e. 81 > 216 is not true
Hence Q > 3/2 is not correct.
Q < 3/2
Therefore P > Q.
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:If f(x) = 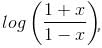 then f(x) + f(y) is equal to
then f(x) + f(y) is equal to
Explanation
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:If 46 + 12 + 18 + 24 + … + 6x = (0.0625)-84, then what is the value of x?
Explanation
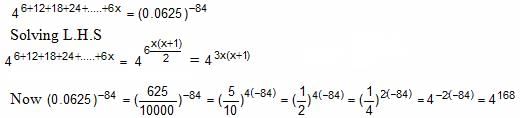
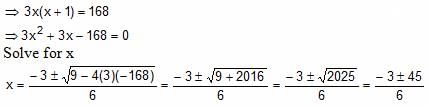
Thus, x = 7, -8
Since x cannot be negative value, x = 7 is the answer.
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:The radioactive decay of a radioactive element is given as per the exponential function A(t) = A0 × eat, where t is half-life of that element and A0 is the amount of the element present initially. In a disastrous nuclear leakage incident in Chernobyl, in 1992, the level of plutonium-80 was found to be 20 times the safe level. If the half-life of plutonium-80 is 20 years, how long will it take for plutonium-80 level to reach the safe limits?
Explanation
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:Find the value of 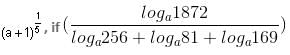 loga961 = 1.
loga961 = 1.
Explanation
Report a problem
Question for Practice Questions Level 3: Exponents & Logarithm
Try yourself:The value of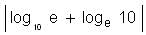 is
is
Explanation
Report a problem
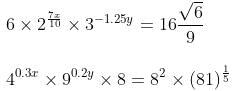
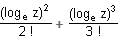 + ... is equal to
+ ... is equal to
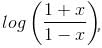 then f(x) + f(y) is equal to
then f(x) + f(y) is equal to
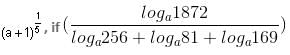 loga961 = 1.
loga961 = 1.
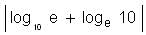 is
is

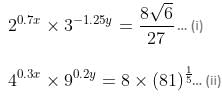
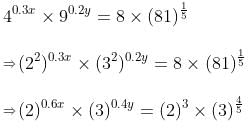
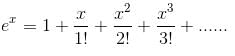
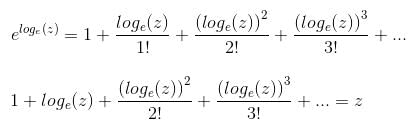
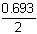 = 0.346
= 0.346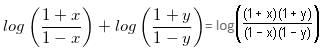
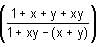
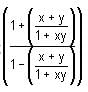
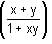
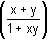
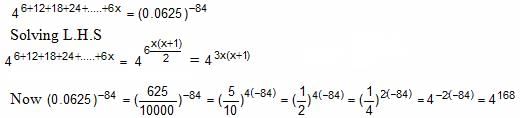
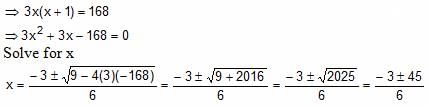
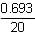 = -0.0346
= -0.0346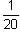 A0 = A0 e-0.346t
A0 = A0 e-0.346t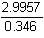 = 8.66 years
= 8.66 years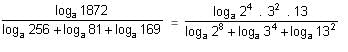
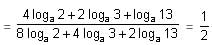
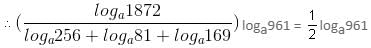
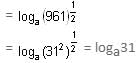
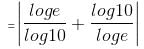
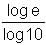 = x, then the given expression can be written as:
= x, then the given expression can be written as: