Daily Practice Questions Questions for CAT with Answers PDF
This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Critical Path (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
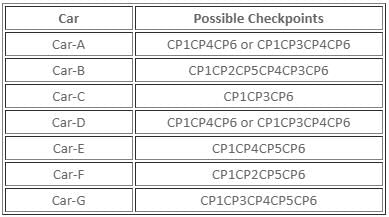
The architectural map below shows the hallways connecting six rooms – R1, R2, R3, R4, R5 and R6 of a certain guest house. However, all the hallways in the map below are not opened to walk at the same time because some maintenance work is going at different hallways during different time of month. Any guest can travel along any hallway only after the hallway is open to walk. The hallways R1R3, R1R2, R2R4, R3R5 and R2R6 are open to walk on week-1, the hallways R1R4 and R5R6 are open to walk on week-2 and the remaining hallways are open to walk on week-3.
After the opening of all the hallways, in how many ways can a person can go from room R1 to room R6 without passing through any room twice ?
The architectural map below shows the hallways connecting six rooms – R1, R2, R3, R4, R5 and R6 of a certain guest house. However, all the hallways in the map below are not opened to walk at the same time because some maintenance work is going at different hallways during different time of month. Any guest can travel along any hallway only after the hallway is open to walk. The hallways R1R3, R1R2, R2R4, R3R5 and R2R6 are open to walk on week-1, the hallways R1R4 and R5R6 are open to walk on week-2 and the remaining hallways are open to walk on week-3.
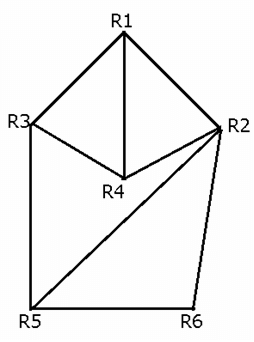
If, in the 1st week, a person travelled from room R4 to room R5, what is the minimum number of rooms that he must have passed through?
The architectural map below shows the hallways connecting six rooms – R1, R2, R3, R4, R5 and R6 of a certain guest house. However, all the hallways in the map below are not opened to walk at the same time because some maintenance work is going at different hallways during different time of month. Any guest can travel along any hallway only after the hallway is open to walk. The hallways R1R3, R1R2, R2R4, R3R5 and R2R6 are open to walk on week-1, the hallways R1R4 and R5R6 are open to walk on week-2 and the remaining hallways are open to walk on week-3.
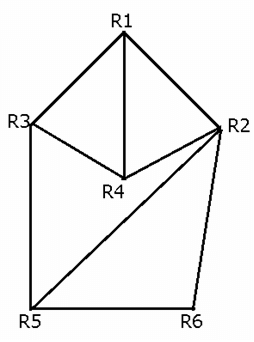
What is the difference between the number of ways that a person can travel from room R1 to room R6 without passing through any room twice in week-2 and that in week-3?
The architectural map below shows the hallways connecting six rooms – R1, R2, R3, R4, R5 and R6 of a certain guest house. However, all the hallways in the map below are not opened to walk at the same time because some maintenance work is going at different hallways during different time of month. Any guest can travel along any hallway only after the hallway is open to walk. The hallways R1R3, R1R2, R2R4, R3R5 and R2R6 are open to walk on week-1, the hallways R1R4 and R5R6 are open to walk on week-2 and the remaining hallways are open to walk on week-3.
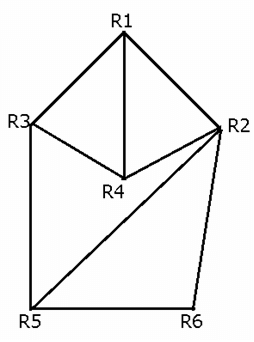
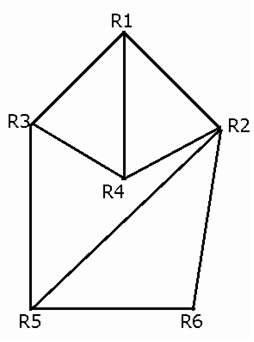
The route taken by which of the following persons would not change in week-3 as compared to that in week-2, if each person passes through the minimum number of rooms and does not pass through any room twice?
How many boats travelled through harbour H4?
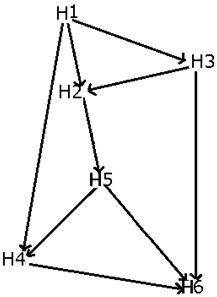
Six Harbors - H1, H2, H3, H4, H5, and H6 - are connected by waterways, as shown in the map below. The arrows represent the direction in which the boats can travel.
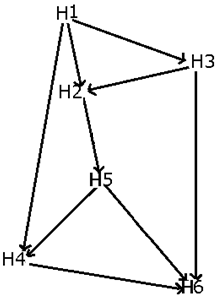
On a particular day, race of one thousand boats was conducted from H1 till H6, passing through different harbors in between. However, no boat passed through the same harbour twice. Further, it is also known that the number of boats which passed through harbour H2 is double the number of boats which passed through H4.
The number of boats which travelled on the waterways connecting harbour H3 and harbour H2 is one-fourth the number of boats which travelled on the waterways connecting harbour H4 and harbour H6.
The number of boats which travelled on the waterways connecting harbour H2 and harbour H5 is double the number of boats which passed through harbour H3.
Exactly 640 boats passed through harbour H5.
Which of the following routes was taken by the maximum number of boats?
Six Harbors - H1, H2, H3, H4, H5, and H6 - are connected by waterways, as shown in the map below. The arrows represent the direction in which the boats can travel.
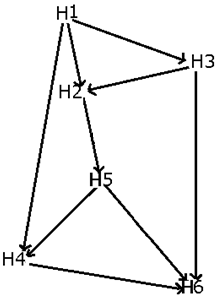
On a particular day, race of one thousand boats was conducted from H1 till H6, passing through different harbors in between. However, no boat passed through the same harbour twice. Further, it is also known that the number of boats which passed through harbour H2 is double the number of boats which passed through H4.
The number of boats which travelled on the waterways connecting harbour H3 and harbour H2 is one-fourth the number of boats which travelled on the waterways connecting harbour H4 and harbour H6.
The number of boats which travelled on the waterways connecting harbour H2 and harbour H5 is double the number of boats which passed through harbour H3.
Exactly 640 boats passed through harbour H5.
Among the following waterways, on which waterway did the maximum number of boats travel?
Six Harbors - H1, H2, H3, H4, H5, and H6 - are connected by waterways, as shown in the map below. The arrows represent the direction in which the boats can travel.
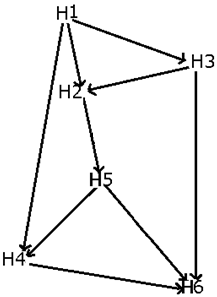
On a particular day, race of one thousand boats was conducted from H1 till H6, passing through different harbors in between. However, no boat passed through the same harbour twice. Further, it is also known that the number of boats which passed through harbour H2 is double the number of boats which passed through H4.
The number of boats which travelled on the waterways connecting harbour H3 and harbour H2 is one-fourth the number of boats which travelled on the waterways connecting harbour H4 and harbour H6.
The number of boats which travelled on the waterways connecting harbour H2 and harbour H5 is double the number of boats which passed through harbour H3.
Exactly 640 boats passed through harbour H5.
What is the number of boats which travelled on the waterways connecting harbour H4 and harbour H6?
Six Harbors - H1, H2, H3, H4, H5, and H6 - are connected by waterways, as shown in the map below. The arrows represent the direction in which the boats can travel.
On a particular day, race of one thousand boats was conducted from H1 till H6, passing through different harbors in between. However, no boat passed through the same harbour twice. Further, it is also known that the number of boats which passed through harbour H2 is double the number of boats which passed through H4.
The number of boats which travelled on the waterways connecting harbour H3 and harbour H2 is one-fourth the number of boats which travelled on the waterways connecting harbour H4 and harbour H6.
The number of boats which travelled on the waterways connecting harbour H2 and harbour H5 is double the number of boats which passed through harbour H3.
Exactly 640 boats passed through harbour H5.
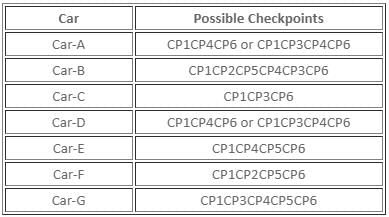
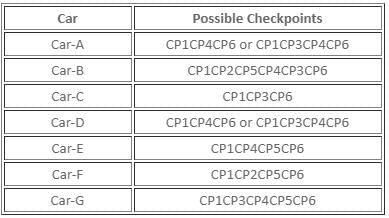
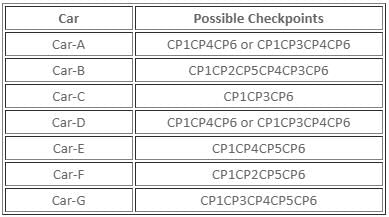
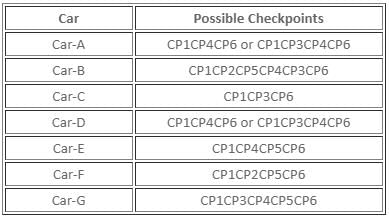
What is the route followed by Car-F?
Six check-points, CP1, CP2, CP3, CP4, CP5, and CP6, are connected by two-way racing tracks, as shown below.
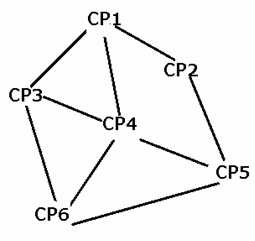
Seven cars, Car-A, Car-B, Car-C, Car-D, Car-E, Car-F, and Car-G, are racing from check-point CP1 to check-point CP6, such that each car passes any check-point at most once. Also, no two cars pass through the same set of check-points when travelling from check-point CP1 to check-point CP6. Further, it is also known that
(i) Car-A and Car-D are the only cars to pass through the track connecting check-point CP4 and check-point CP6.
(ii) While both, Car-B and Car-C, pass through check-point CP3, Car-E does not.
(iii) Car-B is the only car which passes through both, check-point CP2 and check-point CP4, while Car-C does not pass through check-point CP5.
(iv) While Car-F passes from the track connecting check-point CP5 and check-point CP6, it does not pass through check-point CP4.
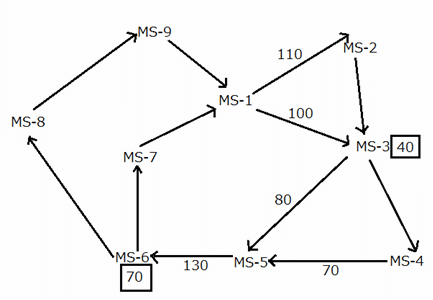
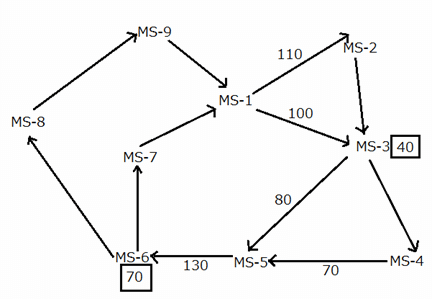
How many passengers are dropped-off at MS-4?
A newly-launched metro line in a certain city has started two metros as per a trial test. Each metro travels to various parts of the city, starting from MS–1, as shown in the map given below. In the map, MS–2 through MS–9 represent the metro stations at which the passengers are being dropped–off. The arrows represent the routes (along with the directions) that the metros take while traveling between metro stations. The metros do not necessarily travel along the same routes, but each route (represented by an arrow) is taken by at least one metro on a given day.
Each metro stops at every location that it comes across on and at least 10 passengers are dropped–off by each metro at every metro station that it stops at. Further, the metros return to the MS–1 after they drop–off all the passengers that they carry from MS–1.
The numbers given in the boxes, at some of the metro stations, represent the total number of passengers being dropped–off at the respective metro stations by the metro(s) that visit that location. The numbers mentioned alongside some of the arrows represent the total number of passengers, being carried by the metro(s), who travel along the respective routes.
It is given that no passenger enters the metros once they start the journey from MS–1.
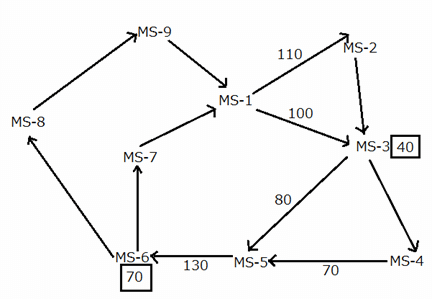
What is the total number of passengers who travel between MS-3 and MS-4?
A newly-launched metro line in a certain city has started two metros as per a trial test. Each metro travels to various parts of the city, starting from MS–1, as shown in the map given below. In the map, MS–2 through MS–9 represent the metro stations at which the passengers are being dropped–off. The arrows represent the routes (along with the directions) that the metros take while traveling between metro stations. The metros do not necessarily travel along the same routes, but each route (represented by an arrow) is taken by at least one metro on a given day.
Each metro stops at every location that it comes across on and at least 10 passengers are dropped–off by each metro at every metro station that it stops at. Further, the metros return to the MS–1 after they drop–off all the passengers that they carry from MS–1.
The numbers given in the boxes, at some of the metro stations, represent the total number of passengers being dropped–off at the respective metro stations by the metro(s) that visit that location. The numbers mentioned alongside some of the arrows represent the total number of passengers, being carried by the metro(s), who travel along the respective routes.
It is given that no passenger enters the metros once they start the journey from MS–1.
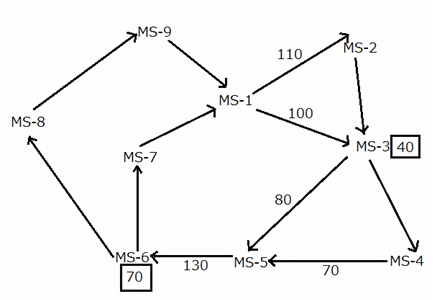
What is the maximum number of passengers that can be dropped-off at MS-8?
A newly-launched metro line in a certain city has started two metros as per a trial test. Each metro travels to various parts of the city, starting from MS–1, as shown in the map given below. In the map, MS–2 through MS–9 represent the metro stations at which the passengers are being dropped–off. The arrows represent the routes (along with the directions) that the metros take while traveling between metro stations. The metros do not necessarily travel along the same routes, but each route (represented by an arrow) is taken by at least one metro on a given day.
Each metro stops at every location that it comes across on and at least 10 passengers are dropped–off by each metro at every metro station that it stops at. Further, the metros return to the MS–1 after they drop–off all the passengers that they carry from MS–1.
The numbers given in the boxes, at some of the metro stations, represent the total number of passengers being dropped–off at the respective metro stations by the metro(s) that visit that location. The numbers mentioned alongside some of the arrows represent the total number of passengers, being carried by the metro(s), who travel along the respective routes.
It is given that no passenger enters the metros once they start the journey from MS–1.
Which of the following tracks did Car-E pass along?
Six check-points, CP1, CP2, CP3, CP4, CP5, and CP6, are connected by two-way racing tracks, as shown below.
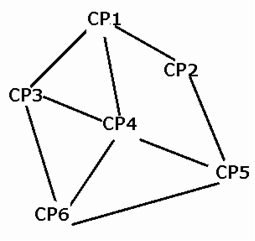
Seven cars, Car-A, Car-B, Car-C, Car-D, Car-E, Car-F, and Car-G, are racing from check-point CP1 to check-point CP6, such that each car passes any check-point at most once. Also, no two cars pass through the same set of check-points when travelling from check-point CP1 to check-point CP6. Further, it is also known that
(i) Car-A and Car-D are the only cars to pass through the track connecting check-point CP4 and check-point CP6.
(ii) While both, Car-B and Car-C, pass through check-point CP3, Car-E does not.
(iii) Car-B is the only car which passes through both, check-point CP2 and check-point CP4, while Car-C does not pass through check-point CP5.
(iv) While Car-F passes from the track connecting check-point CP5 and check-point CP6, it does not pass through check-point CP4.
What is the number of check-points, including CP1 and CP6, through which Car-G passes?
Six check-points, CP1, CP2, CP3, CP4, CP5, and CP6, are connected by two-way racing tracks, as shown below.
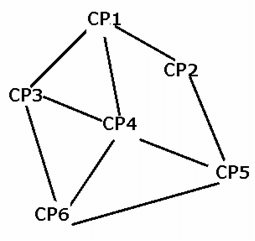
Seven cars, Car-A, Car-B, Car-C, Car-D, Car-E, Car-F, and Car-G, are racing from check-point CP1 to check-point CP6, such that each car passes any check-point at most once. Also, no two cars pass through the same set of check-points when travelling from check-point CP1 to check-point CP6. Further, it is also known that
(i) Car-A and Car-D are the only cars to pass through the track connecting check-point CP4 and check-point CP6.
(ii) While both, Car-B and Car-C, pass through check-point CP3, Car-E does not.
(iii) Car-B is the only car which passes through both, check-point CP2 and check-point CP4, while Car-C does not pass through check-point CP5.
(iv) While Car-F passes from the track connecting check-point CP5 and check-point CP6, it does not pass through check-point CP4.
Which of the following is a correct combination of check-point and the number of cars which pass through that check-point?
Six check-points, CP1, CP2, CP3, CP4, CP5, and CP6, are connected by two-way racing tracks, as shown below.
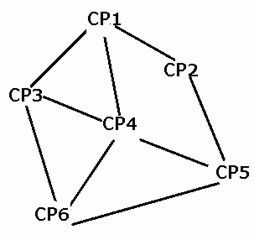
Seven cars, Car-A, Car-B, Car-C, Car-D, Car-E, Car-F, and Car-G, are racing from check-point CP1 to check-point CP6, such that each car passes any check-point at most once. Also, no two cars pass through the same set of check-points when travelling from check-point CP1 to check-point CP6. Further, it is also known that
(i) Car-A and Car-D are the only cars to pass through the track connecting check-point CP4 and check-point CP6.
(ii) While both, Car-B and Car-C, pass through check-point CP3, Car-E does not.
(iii) Car-B is the only car which passes through both, check-point CP2 and check-point CP4, while Car-C does not pass through check-point CP5.
(iv) While Car-F passes from the track connecting check-point CP5 and check-point CP6, it does not pass through check-point CP4.
What is the route followed by Car-C?
Six check-points, CP1, CP2, CP3, CP4, CP5, and CP6, are connected by two-way racing tracks, as shown below.
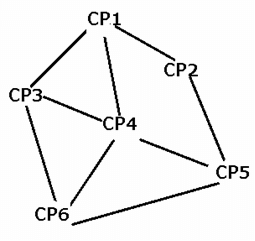
Seven cars, Car-A, Car-B, Car-C, Car-D, Car-E, Car-F, and Car-G, are racing from check-point CP1 to check-point CP6, such that each car passes any check-point at most once. Also, no two cars pass through the same set of check-points when travelling from check-point CP1 to check-point CP6. Further, it is also known that
(i) Car-A and Car-D are the only cars to pass through the track connecting check-point CP4 and check-point CP6.
(ii) While both, Car-B and Car-C, pass through check-point CP3, Car-E does not.
(iii) Car-B is the only car which passes through both, check-point CP2 and check-point CP4, while Car-C does not pass through check-point CP5.
(iv) While Car-F passes from the track connecting check-point CP5 and check-point CP6, it does not pass through check-point CP4.
At which location are the maximum number of passengers dropped-off by both the metros together?
A newly-launched metro line in a certain city has started two metros as per a trial test. Each metro travels to various parts of the city, starting from MS–1, as shown in the map given below. In the map, MS–2 through MS–9 represent the metro stations at which the passengers are being dropped–off. The arrows represent the routes (along with the directions) that the metros take while traveling between metro stations. The metros do not necessarily travel along the same routes, but each route (represented by an arrow) is taken by at least one metro on a given day.
Each metro stops at every location that it comes across on and at least 10 passengers are dropped–off by each metro at every metro station that it stops at. Further, the metros return to the MS–1 after they drop–off all the passengers that they carry from MS–1.
The numbers given in the boxes, at some of the metro stations, represent the total number of passengers being dropped–off at the respective metro stations by the metro(s) that visit that location. The numbers mentioned alongside some of the arrows represent the total number of passengers, being carried by the metro(s), who travel along the respective routes.
It is given that no passenger enters the metros once they start the journey from MS–1.
What is the minimum number of bouncers that the manager must deploy to all the club doors put together, in order to ensure that none of the club doors is destroyed?
The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor club's manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.
The following diagram shows the club doors (B–1 to B–5) and the competitor club's buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.
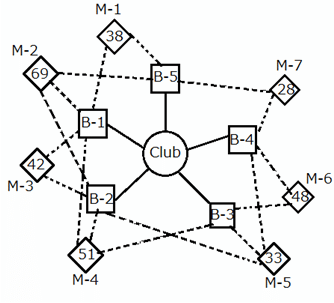
Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.
If the manager wants to save just three club doors from being destroyed, what is the minimum number of bouncers that he must deploy?
The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor club's manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.
The following diagram shows the club doors (B–1 to B–5) and the competitor club's buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.
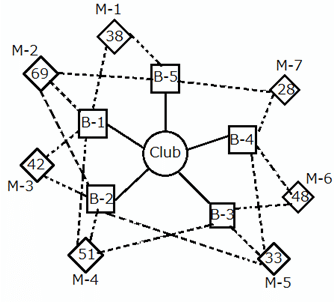
Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.
If it is known that the competitor club is planning to send, from each bus, an equal number of bouncers to all the possible club doors, what is the minimum number of bouncers that will be injured during the attack if no club door should be destroyed?
The famous VIP club of a particular city has five doors. The manager of club has hired some bouncers in order to prevent any type of chaos inside the club. All the bouncers are always present inside the club, unless ordered to move to a door. A competitor club's manager hired some bouncers to damage the club property and enter inside. The bouncers of the competitor club are gathered outside the club, sitting inside buses which are parked in the given pattern, M–1 to M–7. Each bus has a certain number of bouncers. The bouncers from a given bus can attack only some of the doors of the club, as indicated in the diagram below. However, all the bouncers from a single bus of the competitor club need not necessarily attack the same door. The manager has come to know about this and is planning to send his bouncers to the doors.
The following diagram shows the club doors (B–1 to B–5) and the competitor club's buses with bouncers (M–1 to M–7). The solid lines in the figure represent the respective club doors to which the bouncers can be deployed from the club. The dotted lines from each competitor bus represent the doors that the bouncers from that competitor club can attack. The numbers inside each competitor bus represent the number of bouncers inside the bus.
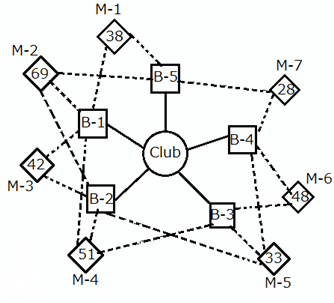
Assume that all the competitor club bouncers attack the club doors that they are assigned to at the same time and that each competitor club bouncer attacks exactly one club door. Also, a higher numerical strength in terms of bouncers will assure victory to any side in such a manner that, if say, 10 competitor club bouncers attack a club door with 11 bouncers, all the competitor club bouncers will be beaten and the club door will remain safe, but with only 1 bouncer remaining. If the number of competitor club bouncers attacking a club door is equal to the number of bouncers at the club door, all the bouncers belonging to both the sides will be beaten, but the club door will remain safe. In a similar manner, if the number of competitor club bouncers attacking is in excess of the number of bouncers, the club door will be destroyed, but with only the excess number of competitor club bouncers remaining not beaten.
|
303 videos|487 docs|279 tests
|