Damped and forced oscillations | Basic Physics for IIT JAM PDF Download
The simple harmonic oscillations discussed above continue forever, at constant amplitude, oscillating as shown in Figure 3 between A and −A. Common experience indicates that real oscillators behave somewhat differently, however. Harmonic oscillations tend to die away as time goes on. This behaviour, called damping of the oscillations, is produced by forces such as friction and viscosity. These forces are known collectively as dissipative forces because they tend to dissipate the potential and kinetic energies of macroscopic bodies into the energy of the chaotic motion of atoms and molecules known as heat.
Figure 3: The function x = A cos ωt.
Friction and viscosity are complicated phenomena whose effects cannot be represented accurately by a general equation. However, for slowly moving bodies, the dissipative forces may be represented by
fd = -yv
where v is the speed of the body and γ is a constant coefficient, independent of dynamic quantities such as speed or displacement. Equation is most easily understood by an argument analogous to that applied to equation above. Fd is written as a sum of powers of v, or Fd(v) = Fd(0) + av + bv2 + · · · . When the body is at rest (v = 0), no dissipative force is expected because, if there were one, it might set the body into motion. Thus, Fd(0) = 0. The next term must be negative since dissipative forces always resist the motion. Thus, a = −γ where γ is positive. Since v2 has the same sign regardless of the direction of the motion, b must equal 0 lest it sometimes contribute a dissipative force in the same direction as the motion. The next term is proportional to v3, and it and all subsequent terms may be neglected if v is sufficiently small. So, as in equation (17) the power series is reduced to a single term, in this case Fd = −γv.
fd = -yv (18)
To find the effect of a dissipative force on a harmonic oscillator, a new differential equation must be solved. The net force, or mass times acceleration, written as md2x/dt2, is set equal to the sum of the Hooke’s law force, −kx, and the dissipative force, −γv = −γdx/dt. Dividing by m yields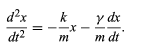 (19)
(19)
The general solution to equation (19) is given in the form x = Ce−γt/2m cos(ωt+ θ0), where C and θ0 are arbitrary constants determined by the initial conditions. This motion, for the case in which θ0 = 0, is illustrated in Figure 4. As expected, the harmonic oscillations die out with time. The amplitude of the oscillations is bounded by an exponentially decreasing function of time (the dashed curves). The characteristic decay time (after which the oscillations are smaller by 1/e, where e is the base of the natural logarithms e = 2.718 . . . ) is equal to 2m/γ. The frequency of the oscillations is given by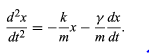
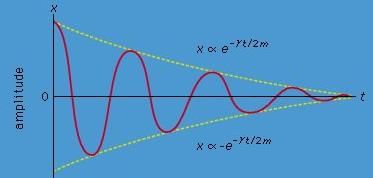
Figure: Damped oscillations.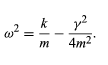
Importantly, this frequency does not change as the oscillations decay.
Equation (20) shows that it is possible, by proper choice of γ, to turn a harmonic oscillator into a system that does not oscillate at all—that is, a system whose natural frequency is ω = 0. Such a system is said to be critically damped. For example, the springs that suspend the body of an automobile cause it to be a natural harmonic oscillator. The shock absorbers of the auto are devices that seek to add just enough dissipative force to make the assembly critically damped. In this way, the passengers need not go through numerous oscillations after each bump in the road.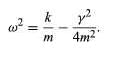 (20)
(20)
A simple disturbance can set a harmonic oscillator into motion. Repeated disturbances can increase the amplitude of the oscillations if they are applied in synchrony with the natural frequency. Even a very small disturbance, repeated periodically at just the right frequency, can cause a very large amplitude motion to build up. This phenomenon is known as resonance.
Periodically forced oscillations may be represented mathematically by adding a term of the form a0 sin ωt to the right-hand side of equation. This term describes a force applied at frequency ω, with amplitude ma0. The result of applying such a force is to create a kind of motion that does not need to decay with time, since the energy lost to dissipative processes is replaced, over the course of each cycle, by the driving force. The amplitude of the motion depends on how close the driving frequency ω is to the natural frequency ω0 of the oscillator. Interestingly, even though dissipation is present, ω0 is not given by equation (20) but rather by equation (15): ω20 = k/m. In a graph of the amplitude of the steady state motion (i.e., long after the driving force has begun to be applied), the maximum amplitude occurs as expected at ω = ω0. The height and width of the resonance curve are governed by the damping coefficient γ. If there were no damping, the maximum amplitude would be infinite. Because small disturbances at every possible frequency are always present in the natural world, every rigid structure would shake itself to pieces if not for the presence of internal damping.
Resonances are not uncommon in the world of familiar experience. For example, cars often rattle at certain engine speeds, and windows sometimes rattle when an airplane flies by. Resonance is particularly important in music. For example, the sound box of a violin does its job well if it has a natural frequency of oscillation that responds resonantly to each musical note. Very strong resonances to certain notes—called “wolf notes” by musicians—occur in cheap violins and are much to be avoided. Sometimes, a glass may be broken by a singer as a result of its resonant response to a particular musical note.
|
210 videos|156 docs|94 tests
|
FAQs on Damped and forced oscillations - Basic Physics for IIT JAM
| 1. What is damped oscillation? |  |
| 2. What causes damping in an oscillating system? |  |
| 3. How does the damping affect the frequency of oscillation? |  |
| 4. What is forced oscillation? |  |
| 5. How does the amplitude of forced oscillation change with the frequency of the applied force? |  |

|
Explore Courses for Physics exam
|

|

















