Decimal Fractions: Notes and Important Formulas | Quantitative Aptitude for SSC CGL PDF Download
| Table of contents |

|
| Definition |

|
| Understanding Decimal Fractions |

|
| Operations on Decimal Fractions |

|
| Practice Questions on Decimal Fractions |

|
Definition
Decimal fractions are a fundamental aspect of mathematics, representing numbers that are less than one but more than zero. They are expressed with a decimal point, where the denominator is typically a power of 10.

Let's explore decimal fractions in detail.
Understanding Decimal Fractions
Decimal fractions are numbers that include a decimal point to indicate values smaller than a whole unit.
For example, numbers like 0.1 (one tenth), 0.25 (twenty-five hundredths), 0.008 (eight thousandths), and 0.333 (three hundred thirty-three thousandths) are all decimal fractions.
The digits to the right of the decimal point represent parts of a whole, such as tenths, hundredths, thousandths, and so forth.

Decimal Fractions:
Decimal fractions are numbers less than one that are expressed using a decimal point. They are fractions where the denominator is a power of 10. Here are some examples: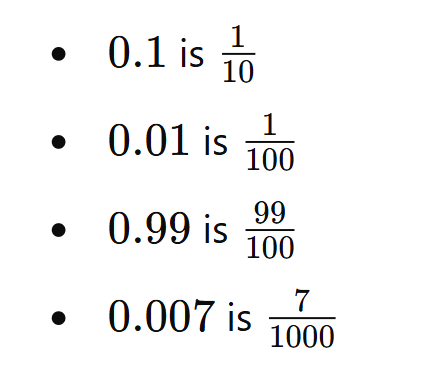
Conversion of Decimal to Vulgar Fraction:
To convert a decimal into a vulgar fraction:
- Put 1 in the denominator under the decimal point and add zeros equal to the number of decimal places.
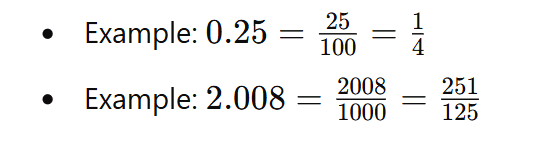
- Annexing Zeros and Removing Decimal Signs:
- Annexing zeros to the right of a decimal fraction doesn't change its value. For example, 0.8=0.80=0.800.
- When the numerator and denominator have the same number of decimal places, the decimal point can be removed.
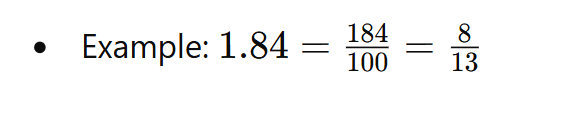
Operations on Decimal Fractions
Addition and Subtraction: Align decimals and perform as usual.
- Example: 5.9632+0.073=6.0362
Multiplication: Multiply without the decimal point, then place the decimal in the product according to the total decimal places.
- Example: 0.2×0.02×0.002=0.000008
Division: Divide as normal and place the decimal in the quotient corresponding to the decimal places in the dividend.
- Example: 0.0204÷17=0.0012
Recurring Decimals: If figures or sets of figures repeat indefinitely, it's a recurring decimal.
- Example: 0.333...=0.3, 3.142857142857...=3.142857
Pure Recurring Decimal: All figures after the decimal point repeat.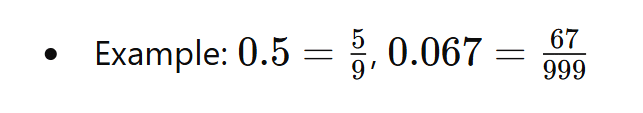 Mixed Recurring Decimal: Some figures repeat while others don't.
Mixed Recurring Decimal: Some figures repeat while others don't.
- Example: 0.173333...=0.173
Decimal fractions are essential in mathematics for precise representation of values less than one. They're used in everyday calculations, finance, science, and more. Understanding their conversion, operations, and recurring nature is crucial for mastering mathematical concepts and applications.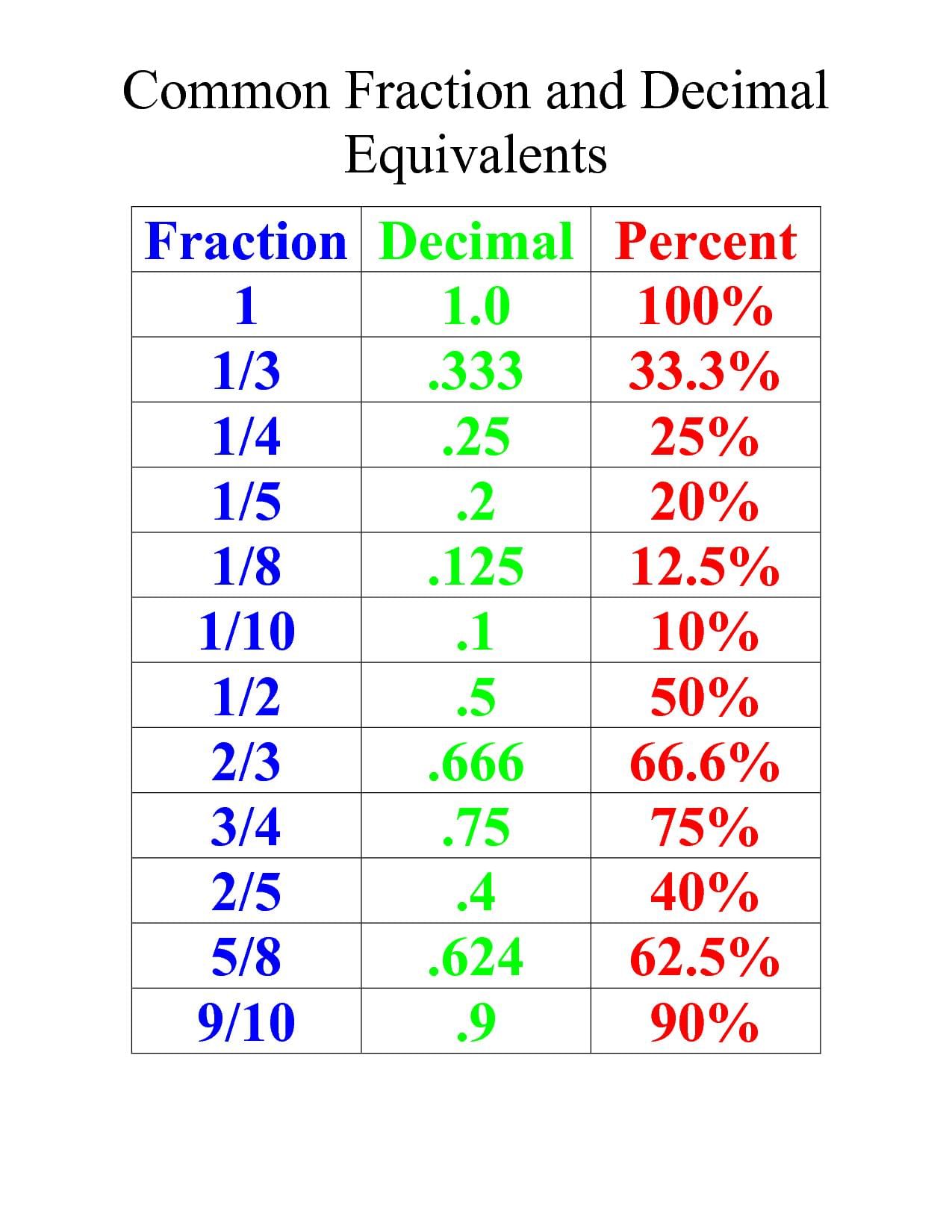
Practice Questions on Decimal Fractions
Question 1: What is the product of 0.003 and 0.4?
Answer: 0.003 × 0.4 = 0.0012
Multiply as if there were no decimals:
3 × 4 = 12.Count the decimal places:
0.003 has 3 decimal places.
0.4 has 1 decimal place. Total decimal places = 3 + 1 = 4.
Place the decimal in the product:
12 → 0.0012.
Question 2: Convert 0.173333... to a fraction.
Answer: 0.173333... = 13/75
Let x = 0.173333...
Multiply both sides by 10:
10x = 1.73333...Subtract the original equation from the new equation:
10x - x = 1.73333... - 0.17333...
9x = 1.56
⇒ x = 1.56/9 = 156/900 = 13/75.
Question 3: What is the product of 0.003 and 0.4?
Answer: 0.003 × 0.4 = 0.0012
Multiply as if there were no decimals:
3 × 4 = 12.Count the decimal places:
0.003 has 3 decimal places.
0.4 has 1 decimal place. Total decimal places = 3 + 1 = 4.
Place the decimal in the product:
12 → 0.0012.
Question 4: What is 3.257 + 4.836?
Align the decimals and add:
Answer: 8.093
Question 5:
What is 9.462 - 3.218?
Align the decimals and subtract:
Answer: 6.244
|
317 videos|290 docs|185 tests
|
FAQs on Decimal Fractions: Notes and Important Formulas - Quantitative Aptitude for SSC CGL
| 1. What are decimal fractions? |  |
| 2. How do you convert a decimal fraction to a common fraction? |  |
| 3. What are some important formulas related to decimal fractions? |  |
| 4. How do you compare decimal fractions? |  |
| 5. How do you round decimal fractions to a certain place value? |  |


















