Degree of Polynomial | Algebra - Mathematics PDF Download

Polynomial in One Variable
The degree of polynomials in one variable is the highest power of the variable in the algebraic expression. For example, in the following equation: x2+2x+4. The degree of the equation is 2 .i.e. the highest power of variable in the equation.
Multivariable polynomial
For a multivariable polynomial, it the highest sum of powers of different variables in any of the terms in the expression. Take following example, x5+3x4y+2xy3+4y2-2y+1. It is a multivariable polynomial in x and y, and the degree of the polynomial is 5 – as you can see the degree in the terms x5 is 5, x4y it is also 5 (4+1) and so the highest degree among these individual terms is 5.
A polynomial of two variable x and y, like axrys is the algebraic sum of several terms of the prior mentioned form, where r and s are possible integers. Here, the degree of the polynomial is r+s where r and s are whole numbers.
Note: Exponents of variables of a polynomial .i.e. degree of polynomials should be whole numbers.
How to find the Degree of a Polynomial?
There are 4 simple steps are present to find the degree of a polynomial:-
Example: 6x5+8x3+3x5+3x2+4+2x+4
- Step 1: Combine all the like terms that are the terms of the variable terms
(6x5+3x5)+8x3+3x2+2x+(4+4) - Step 2: Ignore all the coefficients
x5+x3+x2+x+x0 - Step 3: Arrange the variable in descending order of their powers
x5+x3+x2+x+x0 - Step 4: The largest power of the variable is the degree of the polynomial
deg(x5+x3+x2+x+x0) = 5
Classification Based on the Degree of the Equation
Based on the degree, the equation can be linear, quadratic, cubic, and bi-quadratic, and the list goes on.
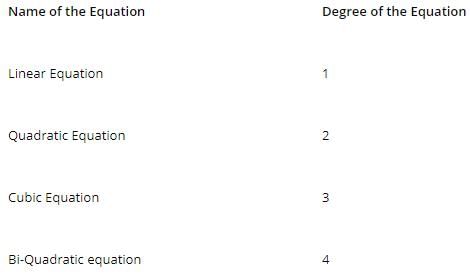
Importance of Degree of polynomial
Case of Homogeneous Polynomial
The degree of terms is a major deciding factor whether an equation is homogeneous or not. A polynomial of more that one variable is said to be homogeneous if the degree of each term is the same. For example, 2x7+5x5y2-3x4y3+4x2y5 is a homogeneous polynomial of degree 7 in x and y.
Relation of Degree of Polynomials with Zeroes of Equation
Theorem 1: A polynomial f(x) of the nth degree cannot vanish for more than n values of x unless all its coefficients are zero.
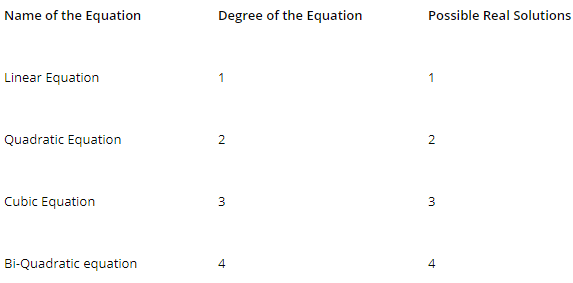
The above table shows possible real zeros /solutions; actual real solutions can be less than the degree of the equation.
Note: A constant polynomial is that whose value remains the same. It contains no variables. The power of the constant polynomial is Zero. Well, you can write any constant with a variable having an exponential power of zero. If the constant term = 4, then the polynomial form is given by f(x)= 4x0
Before going to start other sections of Polynomials, try to solve the below-given question.
A Question for You
Question: Find the degree of polynomial x3+4x5+5x4+2x2+x+5.
Solution: x3+4x5+5x4+2x2+x+5
=4x5+5x4+x3+2x2+x+5
=x5+x4+x3+x2+5
Degree of equation is the highest power of x in the given equation .i.e. 5.
|
161 videos|58 docs
|
FAQs on Degree of Polynomial - Algebra - Mathematics
| 1. What is a polynomial in mathematics? |  |
| 2. How do you determine the degree of a polynomial? |  |
| 3. What is the significance of the degree of a polynomial? |  |
| 4. Can a polynomial have a negative degree? |  |
| 5. What is the difference between linear and quadratic polynomials? |  |




















