Derivatives of Hyperbolic Functions | Calculus - Mathematics PDF Download
The last set of functions that we’re going to be looking in this chapter at are the hyperbolic functions. In many physical situations combinations of ex and e−x arise fairly often. Because of this these combinations are given names. There are six hyperbolic functions and they are defined as follows.
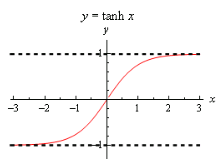
Here are the graphs of the three main hyperbolic functions.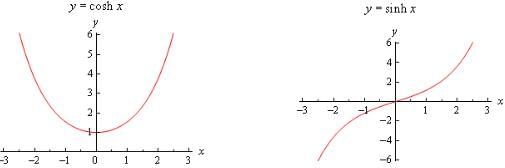
We also have the following facts about the hyperbolic functions.
You’ll note that these are similar, but not quite the same, to some of the more common trig identities so be careful to not confuse the identities here with those of the standard trig functions.
Because the hyperbolic functions are defined in terms of exponential functions finding their derivatives is fairly simple provided you’ve already read through the next section. We haven’t however so we’ll need the following formula that can be easily proved after we’ve covered the next section.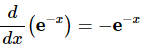
With this formula we’ll do the derivative for hyperbolic sine and leave the rest to you as an exercise.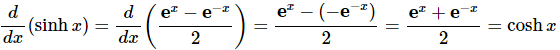
For the rest we can either use the definition of the hyperbolic function and/or the quotient rule. Here are all six derivatives.
Here are a couple of quick derivatives using hyperbolic functions.
Example 1 Differentiate each of the following functions.
(a) f(x) = 2x5 cosh x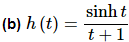
Solution:
(a)
(b) 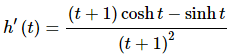
Practice problems: Derivatives Of Hyperbolic Functions
For each of the following problems differentiate the given function.
1. Differentiate f(x) = sinh(x) + 2 cosh(x) − sech(x).
Solution:
Not much to do here other than take the derivative using the formulas from class.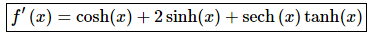
2. Differentiate R(t) = tan(t) + t2csch(t).
Solution:
Not much to do here other than take the derivative using the formulas from class.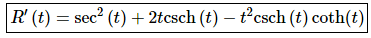
3. Differentiate 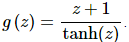
Solution:
Not much to do here other than take the derivative using the formulas from class.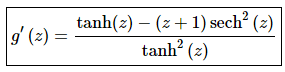
|
112 videos|65 docs|3 tests
|
FAQs on Derivatives of Hyperbolic Functions - Calculus - Mathematics
| 1. What are hyperbolic functions in mathematics? |  |
| 2. What are the derivatives of hyperbolic functions? |  |
| 3. How can hyperbolic functions be used in calculus? |  |
| 4. Are hyperbolic functions similar to trigonometric functions? |  |
| 5. What are the practical applications of hyperbolic functions? |  |

|
Explore Courses for Mathematics exam
|

|

















