Descriptive statistics - Statistics, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
The subject of statistics is broadly divided into two branches: Descriptive Statistics and Inferential Statistics. Descriptive Statistics deals with data collection and summarizing the raw data in an understandable format, and these results are generalized to arrive at a conclusion applying Inferential Statistics. The description or summary of sample behavior, presented using Descriptive Statistics is alone is in turn used for drawing inferences on the Population characteristics. Descriptive Statistics comes into play again in the presentation of the estimated or generalized Population traits.
 The data that is summarized in tabular, graphical or numerical form is also known an descriptive statistics.
The data that is summarized in tabular, graphical or numerical form is also known an descriptive statistics.
Descriptive Statistics:
Descriptive Statistics deals with analysis and methods related to collection, organization, summarizing and presentation of data.
Applying the techniques of descriptive statistics, the raw data is collected and transformed into a meaningful form.
Key Concepts in Descriptive Statistics
1. Measures of Central Tendency:
Mean (Arithmetic Average): The sum of all data values divided by the number of values.
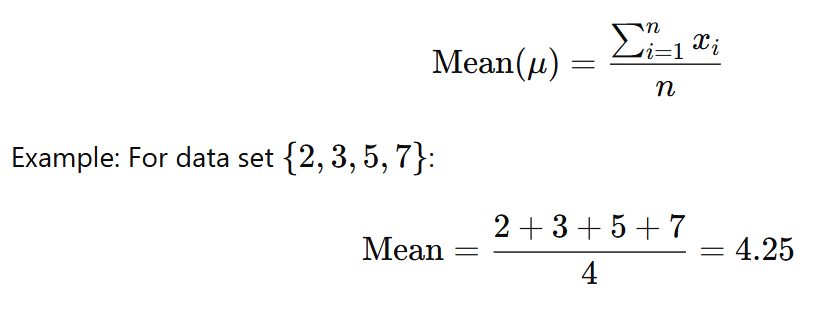
Median: The middle value when data is ordered from least to greatest. For even number of values, it is the average of the two middle numbers.
 Mode: The value that appears most frequently in a data set.
Mode: The value that appears most frequently in a data set.
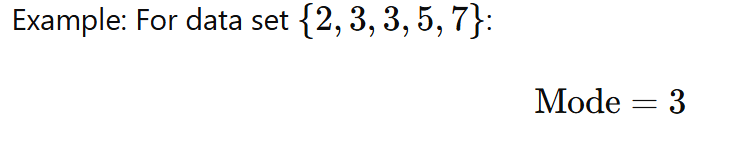
2. Measures of Dispersion:
Range: The difference between the maximum and minimum values in the data set.
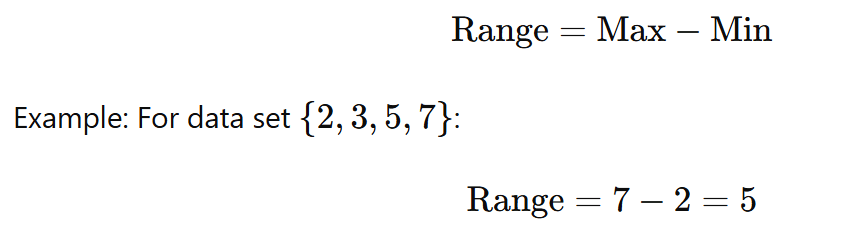
Variance: The average of the squared differences from the mean.
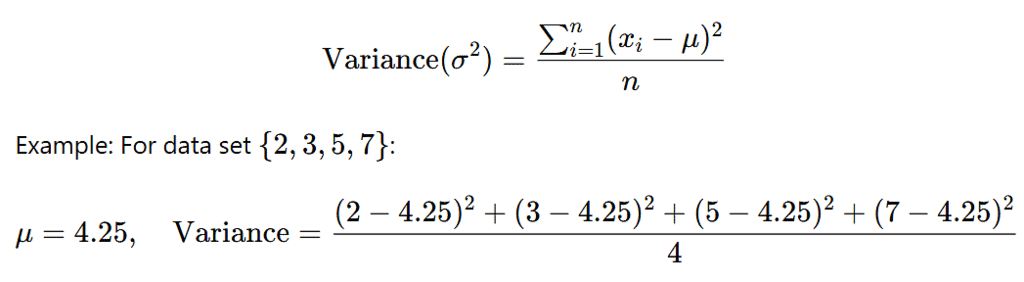
Standard Deviation: The square root of the variance.

3. Measures of Shape:
Skewness: A measure of the asymmetry of the probability distribution of a real-valued random variable about its mean.
Kurtosis: A measure of the "tailedness" of the probability distribution.
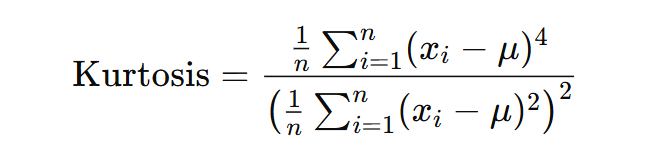
High kurtosis means more of the variance is due to infrequent extreme deviations.
4. Frequency Distribution:
Frequency: The number of times a data value occurs.
Relative Frequency: The fraction or proportion of times a value occurs.
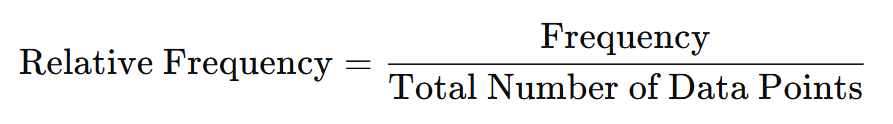
Cumulative Frequency: The sum of the frequencies for all data values less than or equal to a given value.
Solved Example:
Question: In a class of 75 students, a statistics test is conducted for a maximum score of 25. The following table gives the frequencies against the test scores. Find the Mean, Median and Mode for the data.
Test Score | 1 | 5 | 6 | 8 | 10 | 12 | 13 | 14 | 15 | 17 | 20 | 21 | 24 |
Number of | 1 | 1 | 2 | 6 | 10 | 16 | 13 | 9 | 8 | 5 | 2 | 1 | 1 |
Solution:
The Mean of a frequency distribution is calculated using the formula where N is the total number of observations.
We redo the table making suitable columns to enable the required calculations and include a cumulative frequency column (which is used to determine the median).
Test Score | Frequency | fx | Cumulative |
1 | 1 | 1 | 1 |
5 | 1 | 5 | 2 |
6 | 2 | 12 | 4 |
8 | 6 | 48 | 10 |
10 | 10 | 100 | 20 |
12 | 16 | 192 | 36 |
13 | 13 | 169 | 49 |
14 | 9 | 126 | 58 |
15 | 8 | 120 | 66 |
17 | 5 | 85 | 71 |
20 | 2 | 40 | 73 |
21 | 1 | 21 | 74 |
24 | 1 | 24 | 75 |
| ∑f = 75 | ∑fx = 943 |
|
The numbers in the cumulative frequency column against a test score gives the total count of frequencies for test scores equal and less.
Using the formula for mean answer rounded to the tenth.
Hence the average test score = 12.6.
The median is given by the the middle value when the test scores are arranged as an ascending array. That is test score is the median. The 38th item will be a test score 13, as 36 items have scores less than 13 and 49 items have scores less than 14.
Thus the median of the data set = 13.
The test score 12 has the greatest frequency = 16. Hence the mode of the data set is 12.
Question: Given a frequency distribution table, calculate the mean, variance, and standard deviation.
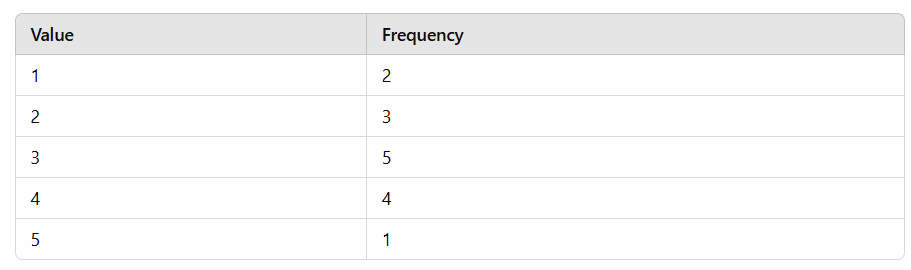
Solution: 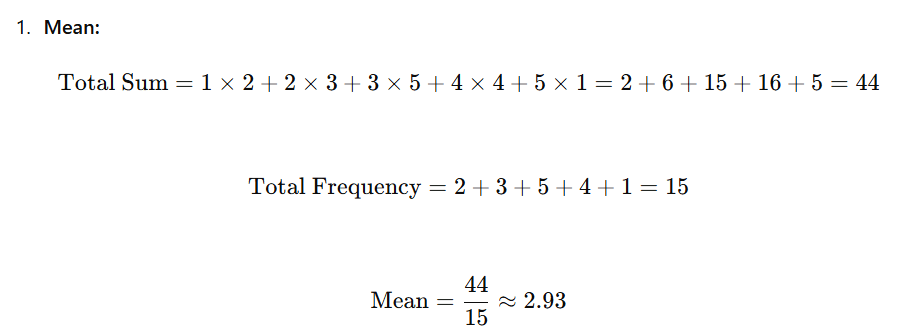
2. Variance
μ=2.93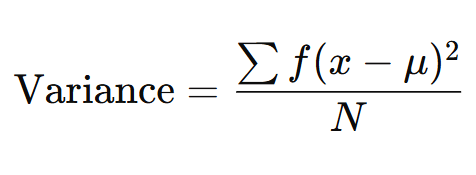
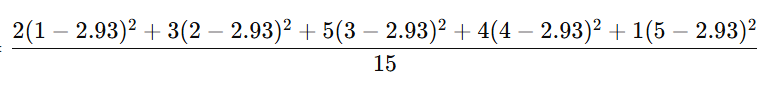
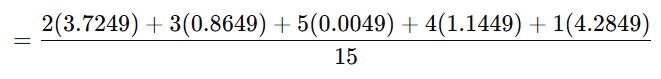
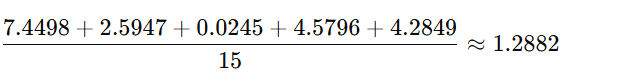

|
556 videos|198 docs
|
FAQs on Descriptive statistics - Statistics, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What are the different types of descriptive statistics? |  |
| 2. How is the mean calculated in descriptive statistics? |  |
| 3. What is the importance of descriptive statistics in mathematics? |  |
| 4. How is the range calculated in descriptive statistics? |  |
| 5. Can descriptive statistics be used to make predictions about future data? |  |






















