Detailed notes: Magnetostatics | Electromagnetic Fields Theory (EMFT) - Electrical Engineering (EE) PDF Download
Introduction
In previous chapters we have seen that an electrostatic field is produced by static or stationary charges. The relationship of the steady magnetic field to its sources is much more complicated. The source of steady magnetic field may be a permanent magnet, a direct current or an electric field changing with time. In this chapter we shall mainly consider the magnetic field produced by a direct current. The magnetic field produced due to time varying electric field will be discussed later. Historically, the link between the electric and magnetic field was established Oersted in 1820. Ampere and others extended the investigation of magnetic effect of electricity . There are two major laws governing the magneto static fields are:
Biot-Savart Law
Usually, the magnetic field intensity is represented by the vector . It is customary to represent the direction of the magnetic field intensity (or current) by a small circle with a dot or cross sign depending on whether the field (or current) is out of or into the page as shown in Fig
Representation of magnetic field (or current)

Biot- Savart Law
This law relates the magnetic field intensity dH produced at a point due to a differential current element 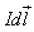 as shown in Fig
as shown in Fig
Magnetic field intensity due to a current element
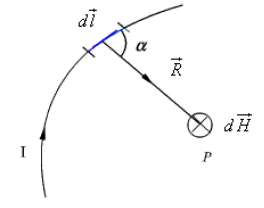
The magnetic field intensity 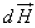 at P can be written as,
at P can be written as,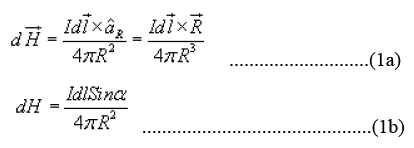
Where 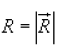 is the distance of the current element from the point P.
is the distance of the current element from the point P.
Similar to different charge distributions, we can have different current distribution such as line current, surface current and volume current. These different types of current densities are shown in Fig
Different types of current distributions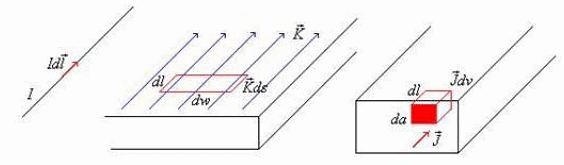
By denoting the surface current density as K (in amp/m) and volume current density as J (in amp/m2) we can write: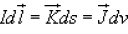 ........(2)
........(2)
( It may be noted that 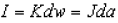 )
)
Employing Biot-Savart Law, we can now express the magnetic field intensity H. In terms of these current distributions.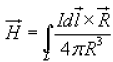 ........for line current........(3a)
........for line current........(3a)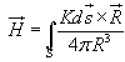 ........for surface current........(3b)
........for surface current........(3b)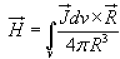 ........for volume current........(3c)
........for volume current........(3c)
MFI due to a straight current carrying filament
Consider an infinitely long conductor AB through which current I flows. Let P be any point at a distance a from the centre of conductor. Consider dl be the small current carrying element at point c at a distance r from point p. α be the angle between r and dl. l be the distance between centre of the coil and elementary length dl. From biot-savart law, magnetic field due to current carrying element dl at point P is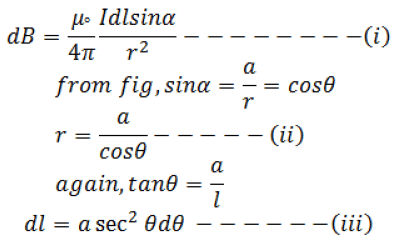
from above three equations
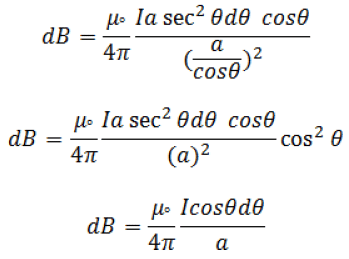
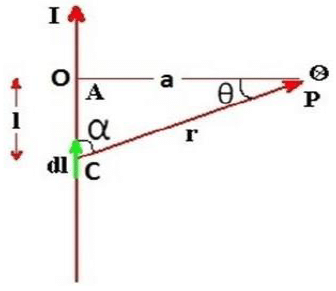
Total magnetic field due to straight current carrying conductor is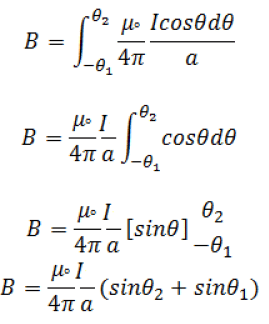
This is the final expression for total magnet c f e d due to staright current carry rig conductor.
If the conductor having infinite length then,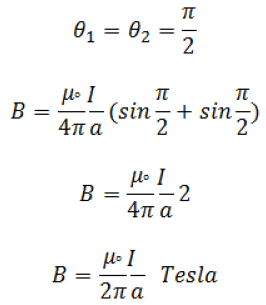
MFI due to circular current Carrying wire
Consider a circular coil having radius a and centre O from which current I flows in anticlockwise direction. The coil is placed at YZ plane so that the centre of the coil coincide along X-axis. P be the any point at a distance x from the centre of the coil where we have to calculate the magnetic field. let dl be the small current carrying element at any point A at a distance r from the point P where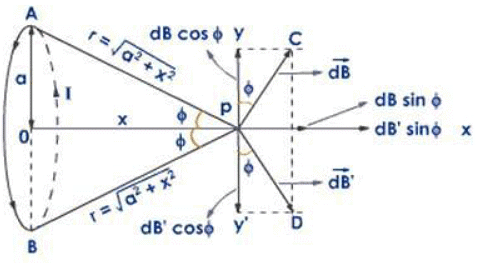
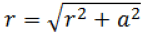
The angle between r and dl is 90°. Then fron biot-savart law, the magnetic field due to current carrying element dl is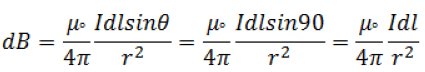
The direction of magnetic field is perpendicular to the plane containing dl and r. So the magnetic field dB has two components
dBcosθ is along the Y — axis
dBsinθ is along the X — axis
Similarly, consider another current carrying element dl’ which is diametrically opposite to the point A. The magnetic field due to this current carrying element dB’ also has two components Here both dBcosθ and dB’cosθ are equal in magnitude and opposite in direction. So they cancle each other. Similarly, the components dBsinθ and dB’sinθ are equal in magnitude and in same direction so they adds up Total magnetic field due to the circular current carrying coil at the axis is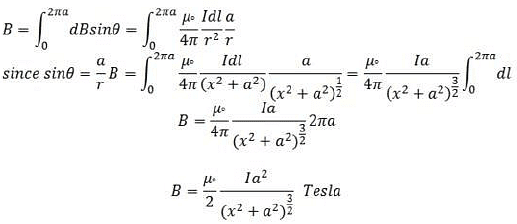
This is the expression for magnetic field due to circular current carrying coil along its axis.
If the coil having N number of turns then magnetic field along its axis is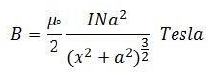
Magnetic Flux Density
In simple matter, the magnetic flux density 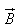 related to the magnetic field intensity
related to the magnetic field intensity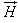 as
as
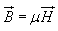 where
where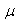 called the permeability. In particular when we consider the free space
called the permeability. In particular when we consider the free space 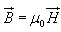 where
where 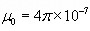 H/m is the permeability of the free space. Magnetic flux density is measured in terms of Wb/m 2 .
H/m is the permeability of the free space. Magnetic flux density is measured in terms of Wb/m 2 .
The magnetic flux density through a surface is given by: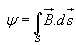 Wb ......................................(15)
Wb ......................................(15)
In the case of electrostatic field, we have seen that if the surface is a closed surface, the net flux passing through the surface is equal to the charge enclosed by the surface. In case of magnetic field isolated magnetic charge (i. e. pole) does not exist. Magnetic poles always occur in pair (as N-S). For example, if we desire to have an isolated magnetic pole by dividing the magnetic bar successively into two, we end up with pieces each having north (N) and south (S) pole as shown in Fig. 6 (a). This process could be continued until the magnets are of atomic dimensions; still we will have N-S pair occurring together. This means that the magnetic poles cannot be isolated.
Subdivision of a magnet
Magnetic field/ flux lines of a straight current carrying conductor
Similarly if we consider the field/flux lines of a current carrying conductor as shown in Fig. (b), we find that these lines are closed lines, that is, if we consider a closed surface, the number of flux lines that would leave the surface would be same as the number of flux lines that would enter the surface.
Maxwell’s second Equation, div(B)=0
From our discussions above, it is evident that for magnetic field,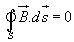 ........(16)
........(16)
which is the Gauss's law for the magnetic field.
By applying divergence theorem, we can write: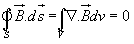
Hence,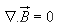 ........(17)
........(17)
Which is the Gauss's law for the magnetic fields in point form.
Ampere's Circuital Law
Ampere's circuital law states that the line integral of the magnetic field 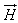 (circulation of H ) around a closed path is the net current enclosed by this path. Mathematically,
(circulation of H ) around a closed path is the net current enclosed by this path. Mathematically,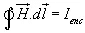 ........(4)
........(4)
The total current I enc can be written as,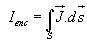 ........(5)
........(5)
By applying Stoke's theorem, we can write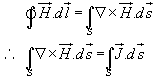 ........(6)
........(6)
Which is the Ampere's law in the point form.
Applications of Ampere's law
We illustrate the application of Ampere's Law with some examples.
Example1 : MFI due to an infinite sheet of current and a long current carrying filament:
We compute magnetic field due to an infinitely long thin current carrying conductor as shown in Fig. 4. Using Ampere's Law, we consider the close path to be a circle of radius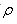 as shown in
as shown in
the Fig. 4.
If we consider a small current element 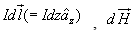 is perpendicular to the plane containing both
is perpendicular to the plane containing both 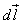 and
and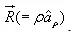 Therefore only component of that
Therefore only component of that 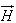 will be present is
will be present is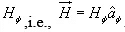
By applying Ampere's law we can write,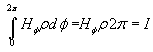 ........(7)
........(7)
Therefore, 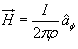 which is same as equation (8)
which is same as equation (8)
Magnetic field due to an infinite thin current carrying conductor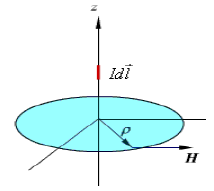
Example2: MFI due to infinitely long coaxial conductor:
We consider the cross section of an infinitely long coaxial conductor, the inner conductor carrying a current I and outer conductor carrying current - I as shown in figure 4.6. We compute the magnetic field as a function of as 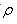 follows:
follows:
In the region 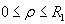
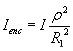 ........(9)
........(9)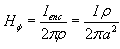 ........(10)
........(10)
In the region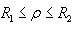
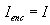
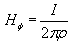 ........(11)
........(11)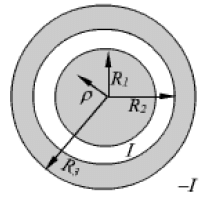
Fig. 5: Coaxial conductor carrying equal and opposite currents
In the region 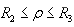
 ........(12)
........(12)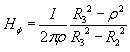 ........(13)
........(13)
In the region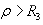
 ........(14)
........(14)
|
10 videos|53 docs|56 tests
|





















