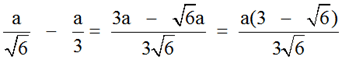Determination of Miller Indices | Physical Chemistry PDF Download
Miller Indices
The orientation of planes or faces in a crystal can be described in terms of their intercepts on the three axes. Miller introduced a system to designate a plane in a crystal.
Miller introduced a set of three numbers to specify a plane in a crystal. This set of three numbers is known as ‘Miller Indices’ of the concerned plane. Miller indices is defined as the reciprocals of the intercepts made by the plane on the three axes.
Procedure for finding Miller Indices
Step 1: Determine the intercepts of the plane along the axes X,Y and Z in terms of the lattice constants a,b and c.
Step 2: Determine the reciprocals of these numbers.
Step 3: Find the least common denominator (lcd) and multiply each by this lcd.
Step 4: The result is written in paranthesis. This is called the `Miller Indices’ of the plane in the form (h k l). This is called the `Miller Indices’ of the plane in the form (h k l).
Illustration
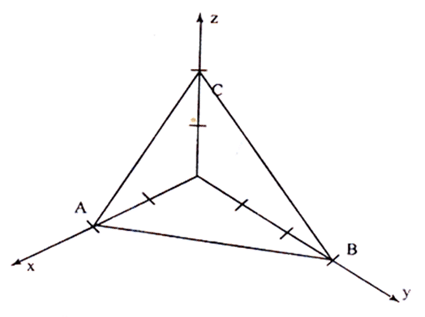
Planes In a Crystal
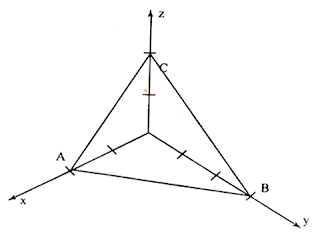
Plane ABC has intercepts of 2 units along X-axis,3 units along Y-axis and 2 units along Z-axis
Determination of ‘Miller Indices’
Step 1: The intercepts are 2,3 and 2 on the three axes.
Step 2: The reciprocals are 1/2, 1/3 and 1/2.
Step 3: The least common denominator is ‘6’. Multiplying each reciprocal by lcd, we get, 3, 2 and 3.
Step 4: Hence Miller indices for the plane ABC is (3 2 3)
Important Features of Miller Indices
For the cubic crystal especially, the important features of Miller indices are, A plane which is parallel to any one of the co-ordinate axes has an intercept of infinity (∞). Therefore the Miller index for that axis is zero; i.e. for an intercept at infinity, the corresponding index is zero.
Example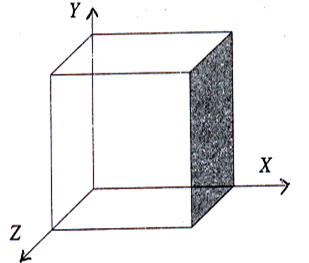 Plane parallel to Y and Z axes
Plane parallel to Y and Z axes
In the above plane, the intercept along X axis is 1 unit. The plane is parallel to Y and Z axes. So, the intercepts along Y and Z axes are ‘∞’.
Now the intercepts are 1, ∞ and ∞.
The reciprocals of the intercepts are = 1/1, 1/∞ and 1/∞.
Therefore the Miller indices for the above plane is (1 0 0).
- A plane passing through the origin is defined in terms of aparallel plane having non zero intercepts.
- All equally spaced parallel planes have same ‘Miller indices’ i.e. The Miller indices do not only define a particular plane but also a set of parallel planes. Thus the planes whose intercepts are 1, 1,1; 2,2,2; -3,-3,-3 etc., are all represented by the same set of Miller indices.
- It is only the ratio of the indices which is important in this notation. The (6 2 2) planes are the same as (3 1 1) planes.
- If a plane cuts an axis on the negative side of the origin, corresponding index is negative. It is represented by a bar, like (1* 0 0). i.e. Miller indices (1* 0 0) indicates that the plane has an intercept in the –ve X –axis.
Miller Indices of Some Important Planes
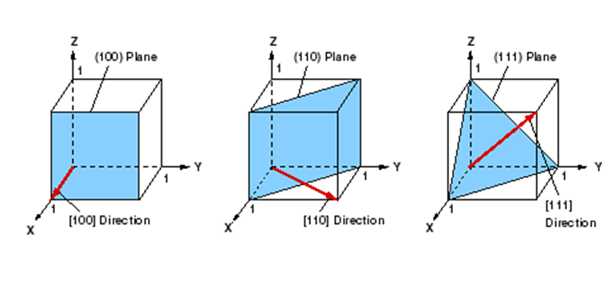
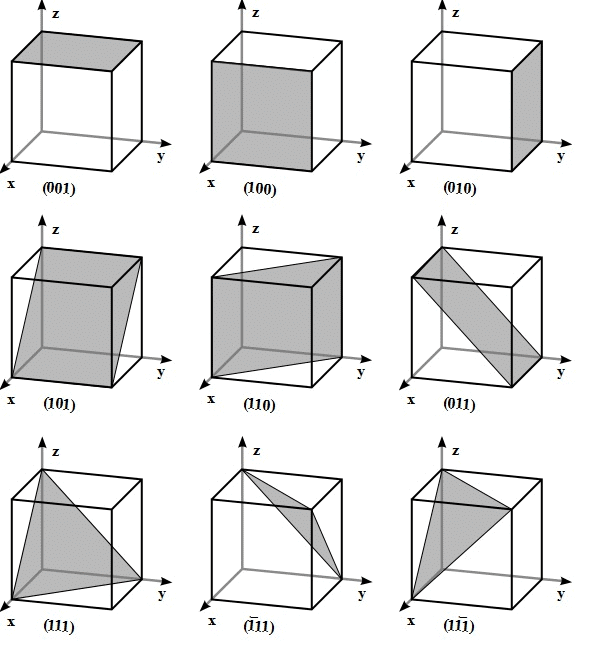
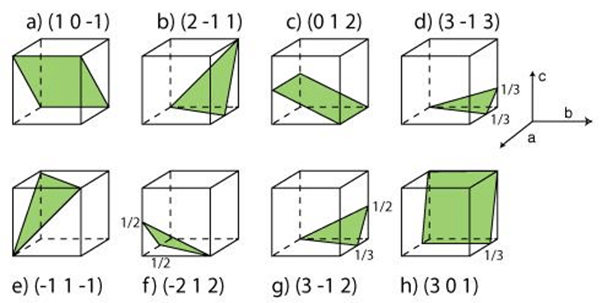
Problem
- If (h k l) is the Miller indices of a crystal plane then the intercepts made by the plane with the crystallographic axes are given as
a/h, b/k and c/1
1. A certain crystal has lattice parameters of 4.24, 10 and 3.66 Å on X, Y, Z axes respectively. Determine the Miller indices of a plane having intercepts of 2.12, 10 and 1.83 Å on the X, Y and Z axes.
Lattice parameters are = 4.24, 10 and 3.66 Å
The intercepts of the given plane = 2.12, 10 and 1.83 Å
i.e. The intercepts are, 0.5, 1 and 0.5.
Step 1: The Intercepts are 1/2, 1 and 1/2.
Step 2: The reciprocals are 2, 1 and 2.
Step 3: The least common denominator is 2.
Step 4: Multiplying the lcd by each reciprocal we get, 4, 2 and 4.
Step 5: By writing them in parenthesis we get (4 2 4)
Therefore the Miller indices of the given plane is (4 2 4) or (2 1 2).
2. Calculate the miller indices for the plane with intercepts 2a, - 3b and 4c the along the crystallographic axes.
The intercepts are 2, - 3 and 4
Step 1: The intercepts are 2, -3 and 4 along the 3 axes
Step 2: The reciprocals are
Step 3: The least common denominator is 12.
Multiplying each reciprocal by lcd, we get 6 -4 and 3 _
Step 4: Hence the Miller indices for the plane is (6,4,3)
Desirable Features of Miller Indices
- The angle ‘q’ between any two crystallographic directions [u1 v1 w1] and [u2 v2 w2] can be calculated easily. The angle ‘q’ is given by,
- The direction [h k l] is perpendicular to the plane (h k l)
- The relation between the interplanar distance and the interatomic distance is given by,
- where h, k and l are the miller indices and a is length of side of cube.
Separation Between Lattice Planes
Consider a cubic crystal of side ‘a’, and a plane ABC. This plane belongs to a family of planes whose Miller indices are (h k l) because Miller indices represent a set of planes. Let ON = d, be the perpendicular distance of the plane A B C from the origin.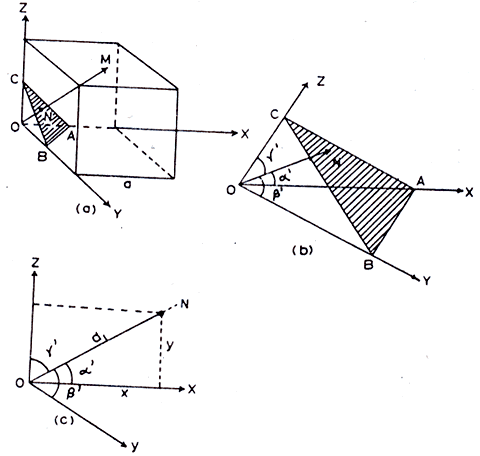
the interplanar spacing between two adjacent parallel planes of Miller indices (h k l ) is given by, NM = OM – ON i.e. Interplanar spacing
Example 1: The lattice constant for a unit cell of aluminum is 4.031Å Calculate the interplanar space of (2 1 1) plane.
a = 4.031 Å
(h k l) = (2 1 1)
Interplanar spacingd = 1.6456 Å
Example 2: Find the perpendicular distance between the two planes indicated by the Miller indices (1 2 1) and (2 1 2) in a unit cell of a cubic lattice with a lattice constant parameter ‘a’.
We know the perpendicular distance between the origin and the plane is (1 2 1)
and the perpendicular distance between the origin and the plane (2 1 2),
The perpendicular distance between the planes (1 2 1) and (2 1 2) are, d = d1 – d2 =
(or) d = 0.0749 a.
|
84 videos|142 docs|67 tests
|
FAQs on Determination of Miller Indices - Physical Chemistry
| 1. What are Miller indices? |  |
| 2. How are Miller indices determined? |  |
| 3. What information do Miller indices provide about crystal planes or directions? |  |
| 4. How can Miller indices be used to identify crystallographic planes? |  |
| 5. Can Miller indices be negative? |  |