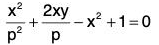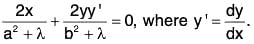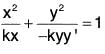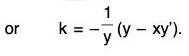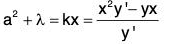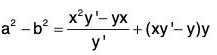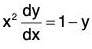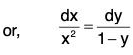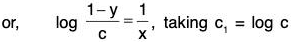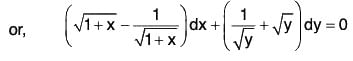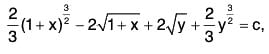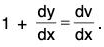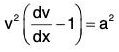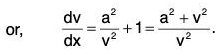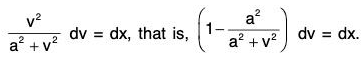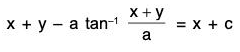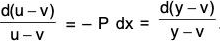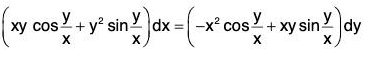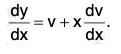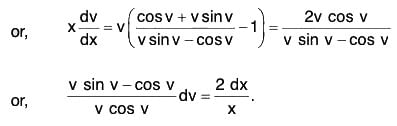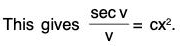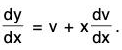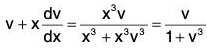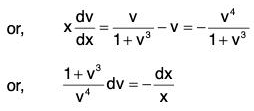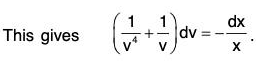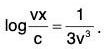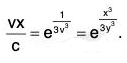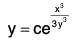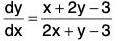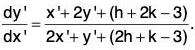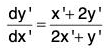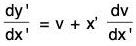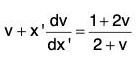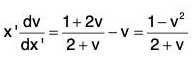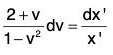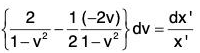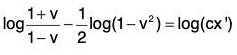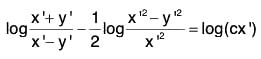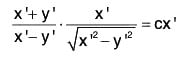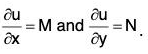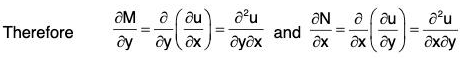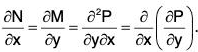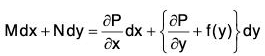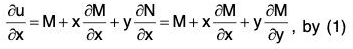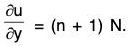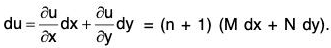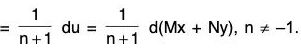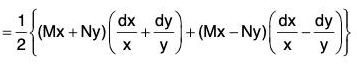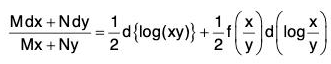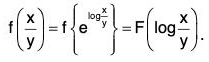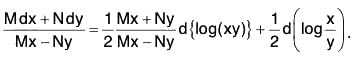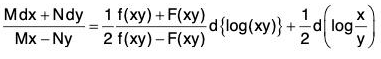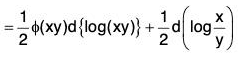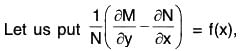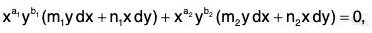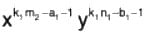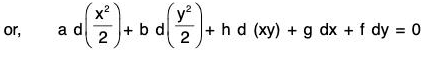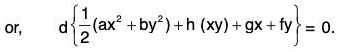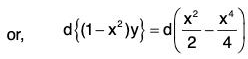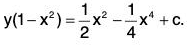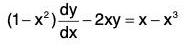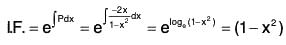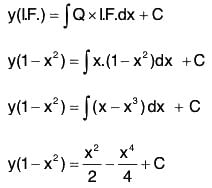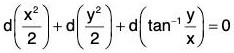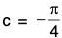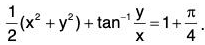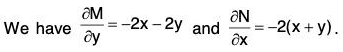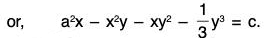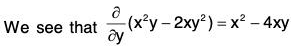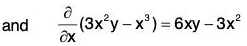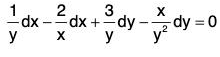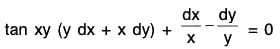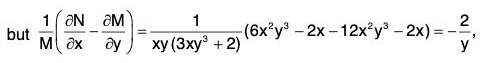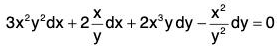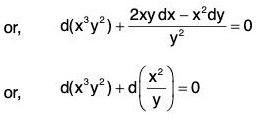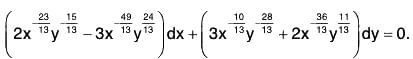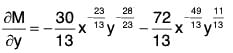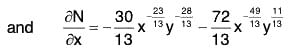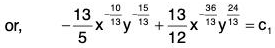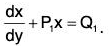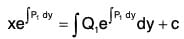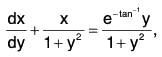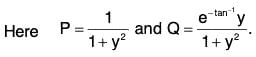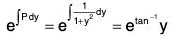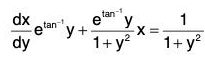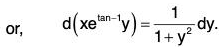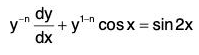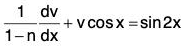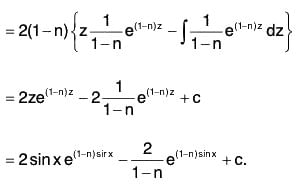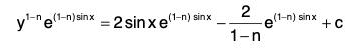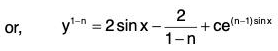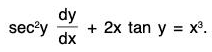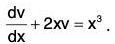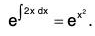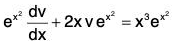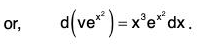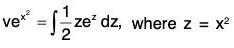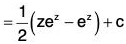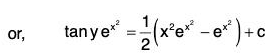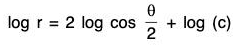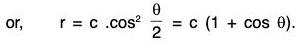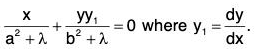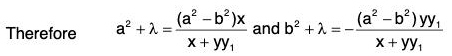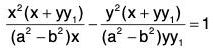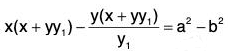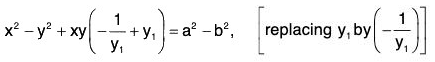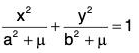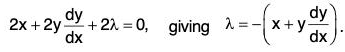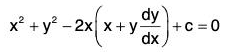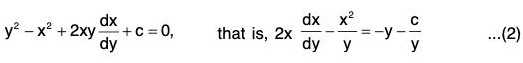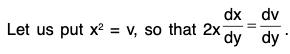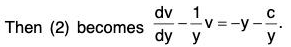Differential Equations- I | Mathematics for Competitive Exams PDF Download

Differential Equations

A relation connecting an independent variable x, a dependent variable y and one or more of their differential coefficients or differentials is called differential equation.
For example,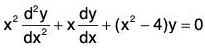

A differential equation as given above which involves only one independent variable is called ordinary differential equations, while those involving more than one independent variables are called partial differential equations. Partial differential equations will involve partial derivatives.
For example,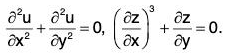

There are differential equations, which do not contain the variables explicitly.
For example,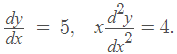

A total differential equation contains two or more dependent variables together with their differentials or differential coefficients with respect to a single independent variable. This may or may not occur explicitly in the equation. In the total differential equation
u dx + v dy + w dz = 0,
where u, v, w are functions of x, y and z, any one of the variables may be regarded as independent and the others as dependent. Thus, taking x as independent variable, the above equation may be written as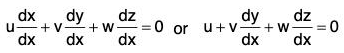

The order of a differential equation is the order of the highest ordered differential coefficient involving in it while the degree of an equation is the greatest exponent of the highest ordered derivative when the equation has been made rational and integral as far as the derivatives are concerned.

Example
(i)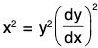  is an equation of first order and second degree.
(ii)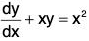  is an equation of first order and first degree;
(iii)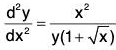  is an equation of second order and first degree;
(iv)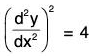  is an equation of second order and second degree;
Let us consider the equation

This equation is to be squared to rationalise it and then it can be easily seen that the greatest exponent of the highest ordered derivative d²y/dx² is two. Hence the equation is of second order and second degree. It should be noted that the determination of the degree does not require the variables x and y to be made rational and integral.
When, in an ordinary or partial differential equation.

Note: In an ordinary or partial differential equations when the dependent variable and its derivatives occur to the first degree only, and not as higher powers or products, the equation is called linear; otherwise it is non-linear. The coefficients of a linear equation are therefore either constants of functions of the independent variable or variables. 

For examples,

are ordinary linear differential equations of the second order while the equations

are ordinary non-linear equations of the first and second order respectively.
Any relation connecting the dependent as well as the independent variables will be called the solution or primitive of the differential equation, if it reduces the differential to an identity when substituted in it. The solution of the differential equation does not contain any derivative. Thus y = 2x is a solution of the differential equation dy/dx = 2.

Formation of differential equations 

Consider the relation y = cx, where c is an arbitrary constant.
Differentiating both sides of this, with respect to x, we get
dy/dx = c.
Eliminating the arbitrary constant from these two, we get the ordinary differential equation
dy/dx = yx        .....(1)
which is of first order and first degree. Substituting y = cx in (1), we see that the equation is identically satisfied, showing that y = cx is a solution of the first equation (1). We notice further that the solution of a differential equation of first order and first degree will involve one arbitrary constant.
In a similar manner, differentiating both sides of the relation
y = A cos (x + B),     .....(2)
dy/dx = - A sin (x + B)      ....(3)
and d²y/dx² = - A cos (x + B)      ....(4)
Eliminating the arbitrary constants A and B from (2) and (4), we get the second ordered ordinary differential equation
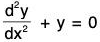     ......(5)
Thus (2) is a solution of the equation (5); for (2), when substituted in (5), reduces it to an identity. As before, we observe that the solution of a differential equation of second order involves two arbitrary constants.
The equations (1) and (5) may be written as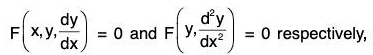

and their solutions are of the forms f(x, y, c) = 0 and f(x, y, A, B) = 0.
Consider now the general relation
f(x, y, c₁, c₂,.... c_n) = 0        ......(6)
which contains, besides the variables x and y, n arbitrary constants
c₁, c₂ ................ c_n 
Differentiating (6) n times in succession, with respect to x, we get

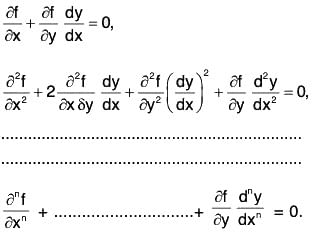
Then, by eliminating the n arbitrary constants from these n equations and the original equation (6), we shall obtain the differential equation

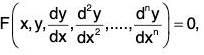
of which (6) is the primitive. This is the typical linear differential equation of order n and degree one.
Thus, if we eliminate the n constants from a relation in x and y involving n arbitrary constants and the n equations arising from its n successive differentiation, then we get the corresponding differential equation, of which the assumed relation in x and y involving n arbitrary constants is the primitive. There being n differentiations, the resulting differential equation will be of n-th order and free from those arbitrary constants.
This shows that a solution of the n-th order ordinary differential equation should involve n arbitrary constants.
On the other hand, the n-th ordered differential equation cannot have more than n arbitrary constants in its primitive. For, if it had (n +1) arbitrary constants, on eliminating them, there would appear an equation of (n + 1)th order and not an equation of the n-th order.

General solution and arbitrary constants 

Assuming the existence of the solution of a differential equation, we consider the differential dy/dx = x. A solution of this equation is  and another solution is    c being a constant, For different values given to c, we get different solutions and in particular, by giving c the value zero, the solution is obtained.
The solutions of the equation are y = cos x and y = sin x.
More general solutions are y = A cos x and y = B sin x, where A and B are constants. The former solutions are obtained from these general solutions by giving A and B the particular value unity. Yet more general solution of the equation is y = A cos x + B sin x, from which all the previous solutions are obtained by giving particular values to the arbitrary constants A and B.
The solution, which contains a number of arbitrary constants equal to the order of the differential equation, is called the general solution, the complete primitive or the complete integral. Solutions obtained from the general solution by giving particular values to the arbitrary constants are called particular solutions.
In some special cases, we get solutions of a differential equation which cannot be derived from its general solution by giving particular values to the arbitrary constants. These solutions are known as singular solutions.
In some linear differential equations, the general solution consists of terms involving the arbitrary constants and terms giving a definite function of the independent variable. The first part is called the complementary function and the remaining part, which can be obtained by giving the value zero to each of the arbitrary constants, is called the particular integral. Thus, if the complete primitive be given by y = A cos x + B sin x + 3e^x, then (A cos x + B sin x) is the complementary function and 3ex is the particular integral.

Note 1. The solution of a differential equation involving arbitrary constants may be expressed in various forms.
Thus log cos x - log (2 - y) = c can be written, on simplification, as y = 2 - k cos x.

Note 2. An arbitrary constant in the solution of a differential equation is said to be independent, if it be impossible to deduce from the solution an equivalent relation which will contain fewer arbitrary constants. Thus the two arbitrary constants a and c in the solution y = ae^x+c are not independent as they are really equivalent to only one; for,
y = ae^{x + c} = ae^x . e^c = Ae^x, where A = ae^c is another constant.
This A is independent.

Note 3. In our above discussion, we have assumed that the conditions, which ensure the existence of the solutions of a given differential equation, are satisfied.

Geometrical significance of differential equation.

Let us consider a differential equation
      .....(1)
of first order and first degree. The primitive of this equation is a relation between two variables x and y and a parameter c, such as
ϕ(x, y, c) = 0,     ...(2)
which, for different numerical values attributed to c, represents different curves. Thus the differential equation represents a single parameter family of curves and each member of this family is called an integral curve.
Now, we know that in Cartesian co-ordinate system, dy/dx of curve gives the direction of the tangent to the curve at a given point. Let the value of dy/dx at a point (x₁, y₁) as given by the equation (1) be m₁. Thus, as a point moves through (x₁, y₁) in the direction m₁ and reaches a point (x₂, y₂) at an infinitesimal distance, then at that point it will move in a direction m₂ as given by (x₂, y₂) and restricted by the equation (1). It will move through an infinitesimal distance to a point (x₃, y₃) and from there under the same condition to (x₄, y₄) and so on through successive points. Thus the point will describe a curve by its movements such that the co-ordinates of any point of the curve and also the value of dy/dx there, will satisfy the differential equation (1). Similar consideration shows that the point will describe some other curve if it starts from some other point on the xy-plane and moves such that the co-ordinates of a point on that curve along with the direction in which it moves satisfy (1). Through every point on the xy-plane, there will pass a particular curve, for every point of which the co-ordinates x, y and the direction of the tangent dy/dx will satisfy the differential equation (1). The equation of each curve is thus a particular solution of the differential equation, the whole system of curves being its general solution which in its totality makes the locus of the differential equation.
If the equation (1) be of second degree in dy/dx , then there will be two values of the direction for each particular point (x₁ , y₁) and hence the point can move through this point in either of these directions and hence two curves of the system, which is the locus of the general solution, will pass through each point. The general solution (2) of the equation must be such that c in that solution must be of second degree.
Generalising this, we can say that a linear differential equation of order one and degree n must contain an arbitrary constant in its general solution whose degree must be n. n of these curves given by the general solution for a particular value of the parameter will pass through each point of the plane. The general solution of a differential equation of second order
     ...(3)
contains two arbitrary constants and therefore the aggregate of integral curves will form a two- parameter family.

Cauchy’s Problem

Or

Ode of the First Order of the Form Y' = F(X, Y)

Consider the first ordered differential equation dy/dx = f(x, y), whose general solution contains one arbitrary constant.
It is sufficient to specify the value y₀ of the particular solution for some value x₀ of the independent variable x, that is, to find a point (x₀, y₀) through which the integral curve of the given equation must pass. But this is not sufficient for equations of higher order. For instance, the general solution of the equation d²y/dx² = 0 is y = Ax + B, where A and B are arbitrary constants.
The equation y = Ax + B defines a two-parameter family of straight lines on the xy-plane. To specify a definite straight line, it is not sufficient to specify a point (x₀, y₀) through which the line must pass. It is also necessary to specify the slope of the line at the point (x₀, y₀) as given by
dy/dx at x = x₀ , that is , (dy/dx)₀.
In the general case of the n-th ordered differential equation
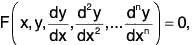     ...(1)
in order to isolate a particular solution, we must have n conditions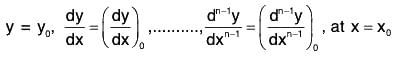
     .....(2)
in which  are given numbers.
Cauchy’s problem is to find a solution of the differential equation (1) which satisfies the specific conditions (2).

Example 1: Eliminate the arbitrary constants A and B from the relation. y = Ae^x + Be^-x + x².

From the given relation, we have
dy/dx = Ae^x - Be^-x + 2x
and d²y/dx² = Ae^x + Be^-x + 2 = y - x² + 2.
Therefore

This is the required differential equation

Example 2: Show that the differential equation satisfied by the family of curves given by c² + 2cy - x² + 1 = 0 , where c is the parameter of the family, is (1 - x²) p² + 2xyp + x² = 0, where p = dy/dx.

From the given equation of the family of curves, we have, on differentiation with respect to x, 2cp - 2x = 0.
Therefore c = x/p.
Eliminating c from the given equation, we get the corresponding differential equation as

or, (1 - x²) p² + 2xyp + x² = 0.

Example 3: Obtain the differential equation of the system of confocal conics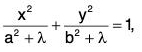

in which λ is the arbitrary parameter and a, b are given constants.

Let us eliminate λ from the given equation and its first derived equation

From the last equation, we have
 .....  (1)
Putting this in the given equation, we have


Substituting this value of k in (1), we get

and b² + X = -kyy’ = y(y - xy’).
Subtracting, we have

Therefore (a² - b²)y’ = x(xy’ - y) + yy’ (xy' - y)
= (xy’ - y) (x + yy’).
This is the required differential equation, whose primitive is the given system of confocal conics.

Equations of First Order and First Degree

Given a differential equation
dy/dx = f(x, y)     .....(1)
where f(x, y) is subject to the following conditions :
(i) f(x, y) is continuous in a given region G,
(ii) I f(x, y) I ≤ M, a fixed real number in G,
(iii) I f(x, y₁) - f(x, y₂) I ≤ k I y₁ - y₂ I, k being a fixed quantity for any two points (x, y₁) and (x, y₂) in the region G.
If now (x₀, y₀) be any point in G such that the rectangular region R as given by lx - x₀l ≤ a, ly - y₀I ≤ b, where b > aM such that R lies wholly within G, then there exists one and only one continuous function y = ϕ(x) having continuous derivatives in lx - x₀l < a, which satisfies the differential equation (1) and takes up the value ϕ(x₀) = y₀ when x = x₀.
The condition (iii), that is, lf(x, y₁) - f(x, y₂)l ≤ k ly₁ - y₂l provided (x, y₁) and (x, y₂) are any two points in G, is known as Cauchy-Lipschitz condition. If f(x, y) admits of continuous partial derivatives and hence 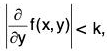 where k is fixed, then the Cauchy-Lipschitz condition is satisfied.
An ordinary differential equation of first order and first degree
dy/dx = f(x, y)
can always be written as M dx + N dy = 0,
Where M and N are functions of x and y. Assuming that the equation has a solution, we shall discuss methods by which the general solutions of these equations can be found in terms of known functions. We classify these equations according to the methods by which they are solved. These classifications are
(A) Equations solvable by separation of variables,
(B) Homogeneous equations,
(C) Exact equations,
(D) Linear equations.

Solution by separation of variables

If the equation M dx + N dy = 0 can be put in the form
f₁(x) dx + f₂(y) dy = 0,
that is, in the separated variables form, then the equation can be solved easily by integrating each term separately. The general solution of the above equation is
∫f₁(x)dx + ∫f₂(x)dy = c,
where c is an arbitrary constant. By giving particular values to c, we shall get particular solutions. The equations of the form
dy/dx = f(x) g(y) or f₁(x) ϕ₁(y) dx + f₂(y) ϕ₂(x) dy = 0
can also be put in the above form and integrated. Sometimes a transformation of the dependent variable will be used to facilitate separation of variables.
Example 1: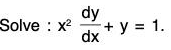

We have, from the given equation


The variables have been separated.
Now, integrating both sides, we get the general solution as
 where c, is an arbitrary constant

or, 1 - y = c e^1/x
or, y = 1 - c e^1/x.

Example 2: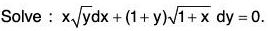

Dividing throughout by  we get

Integrating, we get the general solution as

Example 3: (a) Solve the equation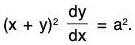
(b) Show that the general solution of the equation 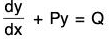 can be written in the form y = k (u - v) + v, where k is a constant and u and v are its two particular solutions.

(a) In this case, we are to apply certain transformation of the dependent variable to have the variables separated.
We put x + y = v, so that  
Putting these in the equation, we get


Separating the variables, we get

Integrating both sides, we get v - a tan^-1 v/a = x + c.

 which is the general solution.
Note. To solve equations of the form dy/dx = f(ax = by + c), the general substitution is ax + by + c = v.
(b) Since u and v are the solutions of     ...(1)
therefore     ...(2)
and    ....(3)
Subtracting (3) from (2), we get
    .....(4)
Subtracting (3) from (1), we get
    .....(5)
From (4) and (5), we have
Integrating, we get log (y - v) = log(u - v) + log k, where k is a constant.
Thus y - v = k(u - v), giving y = k (u - v) + v.

Example 4: The product of the slope and the ordinate at any point (x, y) of a curve passing through the point (5, 3) is equal to the abscissa at that point. Find the equation of the curve.
Find the equation of the curve.

The slope at any point (x, y) of a curve is dy/dx
By the given condition, we have  that is, y dy = x dx.
Integrating, we get x² - y² = c, where c is an arbitrary constant.
Since the curve passes through the point (5, 3), we have c = 25 - 9 = 16.
Therefore the required equation of the curve is x² - y² = 16.

Homogeneous equation.

If a function f(x, y) can be expressed in the form 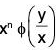 in the form 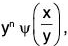then f(x, y) is said to be a homogeneous function degree n in x and y.
If the equation M dx + N dy = 0 can be put in the form

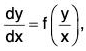
If M and N be homogeneous functions of x and y of same degree, then the equation is called homogeneous. In this case, by y = vx, where v is a function of x, we can change the variable, such that

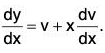
Then, after integration, v is replaced by y/x.

Note. dy/dx = f(x, y) is a homogeneous equation, if f(tx, ty) = f(x, y) for all t.
It can be easily verified that the equations dy/dx = 3 log (x + y) - log (x³ + y³) and  are homogeneous.

Non-homogeneous equation reducible to homogeneous form

Consider a non-homogeneous equation of the form
(a₁x + b₁y + c₁)dx = (a₂x + b₂y + c₂)dy,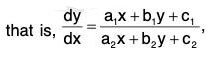
    ....(1)
in a₁/a₂ ≠ b₁/b₂.
This equation can be made homogeneous by the substitution
x = x’ + h and y = y’ + k,
where h and k are constants and are so chosen that
a₁h + b₁k + c₁ = 0         ...(2)
and a₂h + b₂k + c₂ = 0.
The relations (2) determine the constants h and k.
The equation (1) is then reduced to the homogeneous equation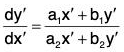

which can be solved after the substitution y’ = vx’ as before,
If a₁/a₂ =  b₁/b₂ ,  then the substitution
a₁x + b₁y = v,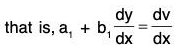

will transform the equation to a form, which can be easily solved.

Example 1: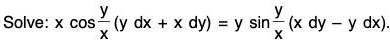  

The given equation can be put as


The equation being homogeneous, let us put y = vx, so that


Integrating both sides, we get log sec v - log v = 2 log x + log c, where c is a constant.

Putting v = y/x , we get the solution as sec y/x = cxy.

Example 2: Solve : x²y dx - (x³ + y³)dy = 0.

Here M and N are homogeneous functions of x and y of degree 3.
The given equation can be written as

Let y = vx, so that
Then the equation becomes


in which the variables v and x have been separated.

Integrating both sides, we get  = - log x + log c, c being a constant
or  
Therefore
Thus the solution is

Example 3: Solve : (x + 2y - 3) dx = (2x + y - 3) dy.

We have the equation

To reduce this to the homogeneous form, let us put x = x’ + h and y = y’ + k, so that dy/dx becomes dy'/dx'
Therefore the equation becomes

Let us choose h and k such that
h + 2k - 3 = 0
and 2h + k - 3 = 0.
These give h = k = 1 and the equation reduces to

which is a homogeneous equation.

We now put y’ = vx' so that
The equation now becomes

or,  
or,  
or,  
Integrating both sides, we get

Putting v = y'/x' , we get

or,
Putting x' = x - 1 and y’ = y - 1 as h = k = 1, we get

or, (x + y - 2)² = c²(x - y)² {(x - 1)² - (y - 1)²}
or, x + y - 2 = c² (x - y)³. 

Exact Equation and its Solution by Inspection

If the differential equation M dx + N dy = 0 can be expressed in the form du = 0, where u is a function of x and y, with out multiplying by any factor, then the equation M dx + N dy = 0 is said to be an exact differential equation and its general solution is u(x, y) = c, where c is an arbitrary constant.
A few exact differentials are given below

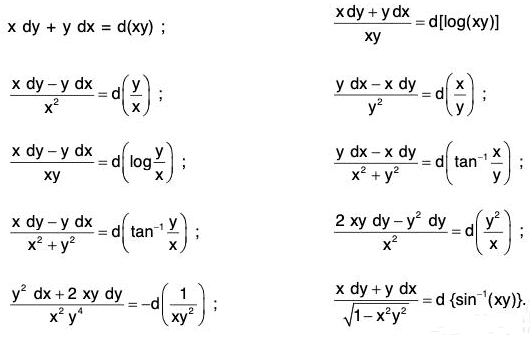
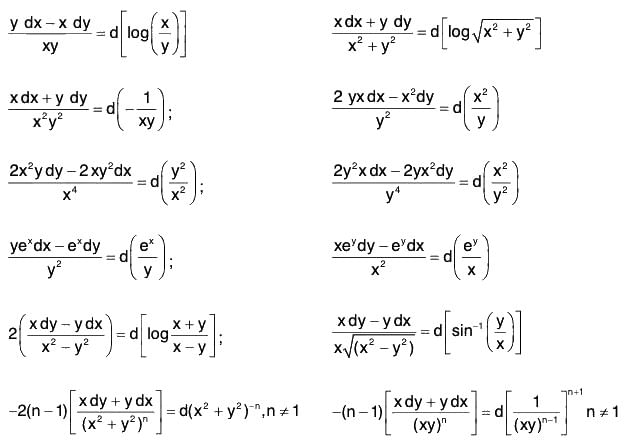
General method of solution of exact equations 

We have stated earlier that the ordinary differential equation M dx + N dy = 0 will be exact, if there exists a function u(x, y), such that M dx + N dy = du. We now establish the condition for that.
Theorem. The necessary and sufficient condition for the ordinary differential equation M dx + N dy = 0 to be exact is

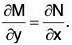
[We assume here that the functions M and N have continuous partial derivatives.]
Proof: If the equation M dx + N dy = 0      ...(1)
be exact, then there must be a function u of x and y, such that
M dx + N dy = du,       ...(2)
a total differential of u = du.
Also, we have        ....(3)
x and y being independent variables.
Now the two expressions (2) and (3) for du are identical and hence, from (2) and (3), we shall have


Hence    ∂M/∂y = ∂N/∂x ,
if the partial derivatives of M and N be continuous.
Thus the condition is necessary.
To prove that this condition is also sufficient, we have to show that if ∂M/∂y = ∂N/∂x , then M dx + N dy = du.
Let us put P = ∫M dx, where, in the integrand, y is supposed to be a constant.
Then ∂P/∂x = M and we have

Therefore  where f(y) is a function of y.
Using these values of M and N, we can write

= d{P + F(y)}, where dF(y) = f(y) dy.
Now, writing P + F(y) = u(x, y), we have M dx + N dy = du.
Thus, to solve an equation of the from M dx + N dy = 0, we have to arrange the terms in groups each of the which is an exact differential, so that u(x, y) may be obtained by inspection only. This method has been discussed earlier.
If this cannot be done, then we have to test the condition ∂M/∂y = ∂N/∂x for the exactness of the equation first.
If it is found to be exact then, to determine the function u(x, y), we use the relation ∂u/∂x = M, which on integration gives u = ∫ M dx + f(y), where f(y) is a function of y.
Now, to determine the function f(y), we equate the total differential of u(x, y) to (M dx + N dy).
We see that all the terms of u(x, y) containing x must appear in ∫ M dx. Hence the differential of this integral with respect to y must have all terms of N dy which contain x. Hence the rule for solving an exact equation of the form M dx + N dy = 0 is
Integrate the terms of M dx considering y as constant ; then integrate those terms of N dy which do not contain x and then equate the sum of these integrals to a constant.
Cor. In the exact equation M dx + N dy = 0, if M and N be homogeneous functions of x and y of degree n (≠ -1), then the primitive can be obtained without any integration and the primitive is Mx + Ny = constant.
Proof: Since the equation is exact, we have ∂M/∂y = ∂N/∂x       ....(1)
Again, since M and N are homogeneous functions of degree n, we have by Euler’s theorem,
          ......(2)
and      .....(3)
Let u = Mx + Ny, so that we have

= M + nM, by (2)
= (n + 1) M.
Similarly, by (1) and (3), we get

Therefore
Hence M dx + N dy
Thus the primitive is Mx + Ny = constant.

Integrating Factors

Sometimes it is seen that an equation, as it stands is not exact but it can be made exact by multiplying it by some function of x and y. The function, which is multiplied to the equation to make it exact, is called integrating factor.
Let M dx + N dy = 0 be an ordinary differential equation and Mx ± Ny = 0.
We have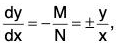
which can be integrated easily and in this situation no integrating factor is necessary. Theorem. The number of integrating factors of an equation M dx + N dy = 0, which has a solution, is infinite.
Proof: Let μ(x, y) be an integrating factor of the equation M dx + N dy = 0, so that μ(M dx + N dy) = du.
Hence μ(x, y) = c is a solution of the equation.
If f(u) be any function of u, then μf(u) (M dx + N dy) = f(u) du.
Now, the right-hand expression is an exact differential, since f(u) du can easily be integrated to give ϕ(u). Thus the solution of the equation is ϕ(u) = c, showing that ϕf(u) is also an integrating factor of the equation M dx + N dy = 0.
Since f(u) is an arbitrary function of u, the number of integrating factors are infinite.

Rules for finding integrating factors 

It is seen that an integrating factor can be found by inspection in simple cases. But in most cases when integrating factor cannot be found by inspection, the following rules are used to find it. For that, we consider the differential equation M dx + N dy = 0, in which ∂M/∂y ≠ ∂N/∂x.
Rule I. If Mx + Ny ≠ 0 and the equation be homogeneous, then 1/(Mx+Ny) is an integrating factor of the equation M dx + N dy = 0.
Proof: We have M dx + N dy

  .....(1)
Since Mx + Ny ≠ 0, we have, dividing both sides by (Mr + Ny),
  ....(2)
Now (Mx + Ny) is homogeneous; hence (Mx - Ny)/(Mx + Ny) is also homogeneous, and is equal to a function of x/y, say f(x/y)
Therefore (2) becomes

  .....(3)
since
The right-hand side of (3) is an exact differential.
Hence we see that 1/(Mx + Ny) is an integrating factor of the equation.
Rule II. If Mx - Ny ≠ 0 and the equation can be written as
{f(xy)} y dx + {F(xy)}x dy = 0, then 1/(Mx - Ny) is an integrating factor of the equation.
Proof: Since Mx - Ny ≠ 0, dividing both sides of (1) by (Mx - Ny), we get

Now, we have M = {f(xy)} y and N = {F(xy)}x.
Therefore


   ...(4)
since ϕ (xy) = ϕ{e^log(xy)} = Ψ {log (xy)}.
The right-hand expression of (4) being an exact differential, 1/(Mx - Ny) is an integrating factor of the equation.

Note. If Mx - Ny = 0 identically, then M/N = y/x and the equation M dx + N dy = 0 reduces to x dy + y dx = 0, whose solution is xy = c.

Rule III. If 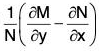 be a function of x along, say f(x), then e^∫f(x)dx is an integrating factor of the equation.
Proof: Let μ be an integrating factor of the equation M dx + N dy = 0, so that (μM) dx + (μN) dy = 0 is an exact differential equation.
Hence the condition  must be satisfied.
This gives     ....(5)
Now suppose μ is a function of x only, so that ∂μ/∂y = 0.
Then (5) gives
  ....(6)
Now, since μ is a function of x alone, the right hand side of (6) is a function of x only.

so that (6) becomes dμ/μ = f(x) dx,
which gives μ = e∫^f(x)dx
Thus   e∫^f(x)dx is an integrating factor of the equation.
Note. e∫^Pdx is is an integrating factor of the equation 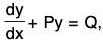 where P and Q are functions of x only, since the equation can be written as (Py - Q) dx + dy = 0, so that M = Py - Q, N = 1 and  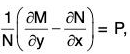which is a function of x alone.
Rule IV.  be a function of y alone, say ϕ(y), then e^∫ϕ(y)dy  is an integrating factor of the equation.
Proof: The proof is similar to that in Rule III.
Rule V. If the equation be of the form x^a y^b (my dx + nx dy) = 0 ; a, b, m, n being constants, then x^{km - a - 1} y^{kn - b - 1}, where k has any value, is an integrating factor of the equation.
Proof: Let us assume that x^p y^q is an integrating factor of the equation x^a y^b (my dx + nx dy) = 0.
Now x^p+a y^q+b (my dx + nx dy) is an exact differential, if (mx^p+a y^q+b+1 dx + nx^p+a+1 y^a+b dy) be an exact differential.
This gives m(q + b + 1) = n(p + a + 1)
or, (q+b+1)/n = (p+a+1)/m = k, say where k is any number.
Therefore p = km - a - 1 and q = kn - b - 1.
Thus we see that x^{km - a - 1} y^{kn = b - 1} where k is any number, is an integrating factor of the equation x^a y^b = (my dx + nx dy) - 0.
In this connection, it should be observed that  is the integral of the exact differential x^{km - 1} y^{kn - 1} (my dx + nx dy).
If the equation can be put in the form

then a factor, that will make the first term an exact differential is
and a factor, that will make the second term an exact differential is   where k₁ and k₂ have any value.
These two factors are identical, if k₁m₁ - a₁ = k₂ m₂ - a₂ and k₁n₁ - b₁ = k₂n₂ - b₂.
These easily determine k₁ and k₂, provided m₁n₂ - m₂n₁ ≠ 0.

Example 1: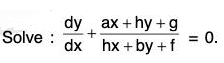

The given equation is (hx + by + f)dy + (ax + hy + g)dx = 0
or, ax dx + by dy + h(x dy + y dx) + g dx + f dy = 0


Integrating, we get 1/2 (ax² + by²) + hxy + gx + fy + c = 0, where c is an arbitrary constant.

Example 2: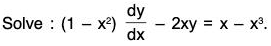

The equation can be written as (1 - x²) dy - 2xy dx = x dx - x³ dx

Integrating both sides, we get

OR

Dividing above equation by (1 - x²).


Now using this formula, we get

Example 3: Solve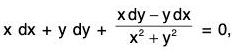 given that y = 1 when x = 1.

The given equation can be put as

Integrating, we get
  ....(1)
where c is an arbitrary constant.
Now, it is given that y = 1 when x = 1.
Putting these in (1), we get 1 + tan^-1 1 + c = 0, giving
Therefore the required particular solution is

Example 4: Examine whether the equation (a² - 2xy - y²)dx - (x + y)² dy = 0 is exact. If it be exact, then find the primitive.

Here M = a² - 2xy - y² and N = -(x + y)².

Hence the equation is exact.
The primitive of the equation is ∫(a² - 2xy - y²)dx + ∫(-y²) dy = 0, y is considered as constant in the first integral

Note. The first integral is ∫M dx and the second integral is ∫(terms not containing x in N) dy.

Example 5: Solve the equation 4x³y dx + (x⁴ + y⁴) dy = 0.

Here ∂M/∂y = 4x3 = ∂N/∂x. Hence the equation is exact.
Furthermore the equation is homogeneous.
Therefore the primitive is Mx + Ny = constant, that is, 5x⁴y + y⁵ = c, where c is a constant,

Example 6: Solve : (x²y - 2xy²) dx + (3x²y - x³) dy = 0.

Therefore the equation is not exact but the coefficients of dx and dy are homogeneous. Hence   will be an integrating factor.
Multiplying both sides of the equation by  we get


Therefore integrating, we get the primitive as

where c is a constant.

Example 7: Solve : (xy sin xy + cos xy) y dx + (xy sin xy - cos xy) x dy = 0.

It is seen that the equation is not exact as ∂M/∂y ≠ ∂N/∂x but M and N are of the forms {f(xy)}y and {F(xy)}x.
Moreover Mx - Ny = 2xy cos xy.
Hence an integrating factor is 1/(2xy cos xy).
Multiplying both sides of the given equation with this integrating factor, we get

or, tan xy d (xy) + d(log x) - d(log y) = 0.
Integrating, we get log sec xy + log x - log y = log c.
 is the primitive, where c is a constant.

Example 8: Solve : (3x²y⁴ + 2xy) dx + (2x³y³ - x²) dy = 0.

Here  ∂M/∂y = 12x²y³ + 2x and ∂N/∂x = 6x²y³ - 2x. So the equation is not exact;

which is a function of y only.
Hence  is an integrating factor of the equation.
Multiplying both sides of the equation by 1/y² , we get

Integrating, we get  c being a constant.

Example 9: Solve the equation (2x²y - 3y⁴) dx + (3x³ + 2xy³) dy = 0.

This equation can be put as x²(2y dx + 3x dy) + y³(-3y dx + 2x dy) = 0.
Here we have a₁ = 2, b₁ = 0, m₁ = 2, n₁ = 3, a₂ = 0, b₂ = 3, m₂ = -3, n₂ = 2.
A factor, that will make the first term an exact differential is  and a factor, that will make the second term an exact differential, is  where k₁ and k₂ have values such that these two factors are same. This gives 2k₁ - 3 = - 3k² - 1 and 3k₁ - 1 = 2k₂ - 4, that is, 2k₁ + 3k₂ - 2 = 0 and 3k₁ - 2k₂ + 3 = 0.
These give  Thus the common factor is x^49/13 y^28/13.
Multiplying by this integrating factor, the equation becomes

Here we see that

Therefore the equation is now exact. Its primitive is  c₁ being a constant

 where c = 60c₁, c is another constant.

Linear Equation

An equation of the form
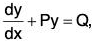   ....(1)
where P and Q are functions of x only (or constants) is called a linear equation of first order in y. The dependent variable and also its derivative in such equations occur in the first degree only and not as higher powers or products.
If both P and Q be constants, then the variables can be easily separated. This will also happen if either P or Q be zero.
Let R be an integrating factor of the above equation. Then the left hand side of the equation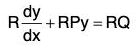  is the differential coefficient of some product. Now the first term  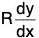can only be derived by differentiating Ry.
We put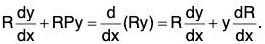

Therefore RP = dR/dx
Integrating, we get logR = ∫P dx , so that R = e^{∫P dx} is an integrating factor.
Now, multiplying both sides of the equation (1) by this integrating factor, we get

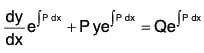
or, d(ye ^{∫P dx}) = Q e^{∫P dx} dx.
On integrating both sides, we get the primitive as ye^{∫P dx} = ∫Qe^{∫P dx} dx+c, where c is a constant.
An alternative form of the solution of the equation (1).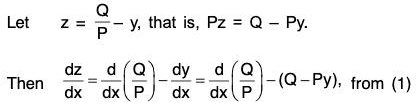



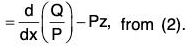
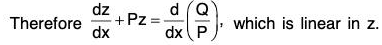
The integrating factor of this equation is e^{∫P dx}. Multiplying the equation by the integrating factor e^{∫P dx}, we get

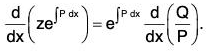
On integration, we get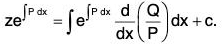
Putting for z, we get an alternative form for the solution of the equation (1) as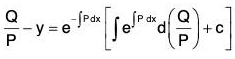

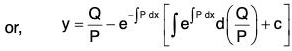
Note. Sometimes an equation may be linear in x, where y is the independent variable. The form of such an equation is

Equation Reducible to Linear Form Or Bernoulli’s Equation

Let us consider the equation 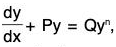 which is known as Bernoulli’s equation, in which P and Q are functions of x alone or constants.
It can be put ax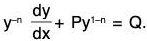
This equation may be brought to the linear form by the substitution

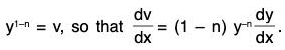
Thus the equation transforms to 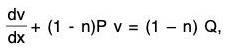 which is linear in v, its integrating factor being e^{(1-n)∫P dx}
The solution is given by ve^{(1-n)∫P dx} = (1 - n) ∫Qe^{(1-n)∫P dx} dx + c.
Then we put y^{1 - n} for v.

Example 1: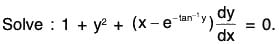

The equation can be written as

which is linear in x.

Integrating factor is

Multiplying both sides of the equation by this integrating factor, we get


Integrating both sides, we get the general solution as xe,^tan-1y = tan^-1y + c. 

Example 2:

We divide both sides of the equation by yⁿ and we get,

Put y^1-n = v, so that  and the equation becomes


Integrating factor of this linear equation in v is e^{∫(1-n)cos dx} = e^{(1-n)sin x}
The solution of this equation is thus
ve^{(1-n)sin x}  = ∫(1 - n)e^{(1-n)sin x} sin 2xdx   .....(1)
Now, to evaluate the right hand side integral, we put sin x = z, so that cos x dx = dz.
Therefore (1 - n)∫ 2e^{(1-n)sin x} sin x cos x dx = 2(1 - n)∫e^(1-n)zz dz

Putting v = y^{1 - n} in (1), we get the general solution of the given equation as

Example 3: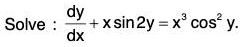

Dividing both sides of the equation by cos² y, we get

We put tan y = v, so that  and the equation becomes

Integrating factor of this equation is
Multiplying both sides of the equation by this integrating factor, we get


Integrating both sides, we get



 is the general solution.

Orthogonal and Oblique Trajectories

Orthogonal Trajectories 

Let F(x, y, c) = 0 be a given one parameter family of curves in the xy plane. A curve that intersects the curves of the family at right angles is called on Orthogonal trajectory of the given family.
Procedure for finding the Orthogonal Trajectories of a given family of Curve
Step 1. From the equation F(x, y, c) = 0   ...(1)
of the given family of curves, find the differential equation dy/dx = f(x, y) of this family.
Step 2. In the differential equation dy/dx = f(x, y)so found in Step 1, replace f(x, y) by its negative reciprocal -1/f(x,y). This gives the differential 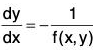 equation of the orthogonal trajectories.
Step 3. Obtain a one-parameter family G(x, y, z) = 0 or y = F(x, c) of solutions of the differential equation (1). Thus obtaining the desired family of orthogonal trajectories (except possibly for certain trajectories that are vertical lines and must be determined separately).

Oblique Trajectories

Definition
Let F(x, y, c) = 0     ...(1)
be a one-parameter family of curves. A curve that intersects the curves of the family (1) at a constant angle α ≠ 90° is called an oblique trajectory of the given family.
Suppose the differential equation of a family is dy/dx = f(x, y)    ...(2)
Then the curve of the family (2) through the point (x, y) has slope f(x, y) at (x, y) and hence its tangent line has angle of inclination tan^-1 [f(x, y)] there, The tangent line of an oblique trajectory that intersects this curve at the angle a will thus have angle of inclination tan^-1[f(x, y)] + α at the point (x, y).
Hence the slope of this oblique trajectory is given by 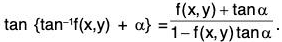Thus the differential equation of such a family of oblique trajectories is given by  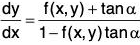Thus to obtain a family of oblique trajectories intersecting a given family of curve at the constant angle α ≠ 90°, we may follow the three step in the above procedure for finding the orthogonal trajectories, except that we replace Step 2 by the following step:
Step 2. In the differential equation dy/dx = f(x, y) of the given family. Replace f(x, y) by the expression.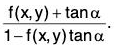

    ...(3)

Example. Consider the family of circles
x² + y² = c²     ...(1)
with centre at origin and radius c. Each straight line through origin
y = kx      ...(2)
is an orthogonal trajectory of the family of circles (1).
is the family of straight lines
y = kx    ....(3)
Let us verify this using the procedure outlined above.
Step 1. Differentiating the equation
x² + y² = c²     ...(4)
of the given family, we obtain

From this we obtain the differential equation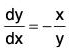
    ...(5)
of the given family (4). (note that the parameter c was automatically eliminated in this case.)
Step 2. We replace - x/y by its negative reciprocal y/x in the differential equation (5) to obtain the differential equation
dy/dx = y/x     ...(6)
of the orthogonal trajectories.
Step 3. We now solve the differential equation (6). Separating variables, we have
y = kx      ...(7)
This is a one-parameter family of solutions of the differential equation (6) and thus represents the family of orthogonal trajectories of the given family of circles (4) (except for the single trajectory that is the vertical line x = 0 and this may be determined by inspection).

Example 1: Find the orthogonal trajectories of the family of cardioids r = a (1 - cos θ), a being a variable parameter.

From the given equation, we get by differentiating with respect to θ.
dr/dθ = a sinθ   ...(i)
Eliminating a, we get      ...(ii)
This is the differential equation of the given family of curves.
To get the differential equation of the system of orthogonal trajectories, we replace  in (ii). Thus we have

Integrating both sides, we get the family of orthogonal trajectories as

Example 2: Show that the family of confocal conics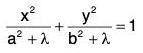 is self-orthogonal, where λ is a parameter.

Differentiating both sides of the given equation with respect to x, we get

This gives x(b² + λ) + yy₁ (a² + X) = 0
or,

Eliminating λ from the given equation, we get the differential equation of the family of curves as

or,
or,    ....(1)
Hence the differential equation of the family of orthogonal trajectories is

which is the same equation as (1) and therefore must have the same primitive.
The equation of the family of orthogonal trajectories is thus

which represents a set of conics confocal with the given set.
Thus the system of confocal conics is self-orthogonal.

Example 3: Show that the orthogonal trajectories of the system of co-axial circles x² + y² + 2λ x + c = 0 forms another system of co-axial circles x² + y² + 2μ y - c = 0, where λ and μ are parameters and c is a given constant.

Differentiating both sides of the given equation with respect to x, we get

Eliminating X from the given equation, we get

or,    ....(1)
which is the differential equation of the given co-axial system of circles.
Replacing  we get the differential equation of the corresponding orthogonal trajectory as



This is a linear equation in v, whose integrating factor is e^{-log y} = 1/y.
Multiplying both sides by 1/y and integrating, we get

where k is a constant.
Now, putting x² for v, we get
x² = -y² + c + ky
or,   x² + y² + 2μ y - c = 0, where k = -2μ.
This is another system of co-axial circles.