Differential Equations | Engineering Mathematics - Engineering Mathematics PDF Download
Definition of Differential Equation
- A differential equation is a special kind of equation that includes terms involving the derivatives of one variable (known as the dependent variable) with respect to another variable (known as the independent variable).
- For instance, in the equation dy/dx = f(x), "x" is the independent variable, and "y" is the dependent variable.
- Differential equations can have either partial derivatives or ordinary derivatives. The derivative measures the rate of change, and the differential equation expresses a relationship between a quantity that changes continuously and the change in another quantity.
- There are various formulas and methods to solve these differential equations and find solutions for the derivatives.

Order of a differential equation
- Order of a differential equation is defined as the order of the highest order derivative of the dependent variable with respect to the independent variable involved in the given differential equation. Consider the following differential equations:
dy / dx = ex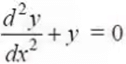
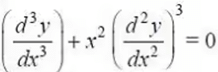
- The first, second, and third equations involve the highest derivative of first, second, and third order respectively. Therefore, the order of these equations are 1, 2, and 3 respectively.
Degree of a differential equation
- By the degree of a differential equation, when it is a polynomial equation in derivatives, we mean the highest power (positive integral index) of the highest order derivative involved in the given differential equation.
- To study the degree of a differential equation, the key point is that the differential equation must be a polynomial equation in derivatives, i.e., y′, y″, y″′ etc. Consider the following differential equations:
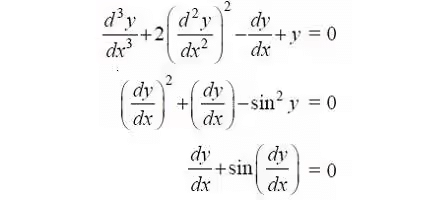
- We observe that first equation is a polynomial equation in y″′, y″ and y′ with degree 1,.
- Second equation is a polynomial equation in y′ (not a polynomial in y though) with degree of 2. Degree of such differential equations can be defined.
- But third equation is not a polynomial equation in y′ and degree of such a differential equation can't be defined.
Note: Order and degree (if defined) of a differential equation are always positive integers.
Example Find the order and degree, if defined, of each of the following differential equations:
(i) dy/dx - cosx = 0
(ii) xy d2y/dx2 + x(dy/dx)2 - ydy/dx = 0
(ii) y''' + y2 + ey = 0
Solution
(i) The highest order derivative present in the differential equation is dy / dx, so its order is one. It is a polynomial equation in y′ and the highest power raised to dy / dx one, so its degree is one.
(ii) The highest order derivative present in the given differential equation is d2y / dx2, so its order is two. It is a polynomial equation in d2y / dx2and dy/dx and the highest power raised to d2y / dx2 is one, so its degree is one.
(iii) The highest order derivative present in the differential equation is y′′′, so its order is three. The given differential equation is not a polynomial equation in its derivatives and so its degree is not defined.
Separable differential equation
y' = A(x)B(y)
Example:
y' = y2 e-x ⇒ y = 1/(e-x+ c)
RC circuits:
- Charging:
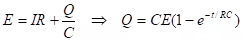
- Discharging: IR = Q/C ⇒ Q = Qoe-1/RC
Linear Differential Equations
y'(x) + p(x)y(x) = q(x)
Integrating factor
I.F. = e∫p(x)dx
The solution of the Differential Equation written above is given by:
y.(I.F.) = ∫q(x). (I.F. )dx + c
Example: Solve, y' = 3x2- y/x y(1) = 5
Sol: y' + y/x = 3x2
I.F. = e∫1/xdx = elnx = x
Therefore, y.x = ∫3x2.x dx+ c
yx = 3x4/4 + c
Now y(1) = 5
Hence, 5x1 = 3x1/4 + c
c = 5-3/4 = 17/4
There the solution of a given differential equation is y(x) = 3x4/4 + 17/4
Exact Differential Equations
(a) Potential function
For M(x, y) + N(x, y)y' = 0 we can find a ∅(x, y) such that d∅/dx = M and d∅ / dy = N; is the potential function; M(x, y) + N(x, y)y' is exact.
(b) Exact differential equation
A potential function exists; general solution: ∅(x, y) =
Example: 
Theorem: Test for exactness: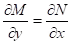
Example: x2 = 3xy + (4xy + 2x)y'= 0
ex sin y - 2x + (ex cosy + 1)y' = 0
Integrating Factors
(a) Integrating factor: μ(x, y) ‡ 0 such that μM(x,y) + μN(x,y)y' = 0 is exact.
Example: y2 - 6xy + (3xy - 6x2)y' = 0
(b) How to find integrating factor: 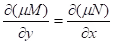
Example: x - xy - y'= 0
A. Separable equations and integrating factors: μ= 1/B
B. Linear equations and integrating factors: I.F. = e∫p(x)dx
Homogeneous and Bernoulli Equations
(a) Homogeneous differential equation:
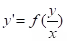 ; let y = ux⇒ separable.
; let y = ux⇒ separable.Example: 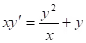 .
.
(b) Bernoulli equation:  y' = P(x)y = R(x)yα; α= 0 ⇒ linear;α= 1
y' = P(x)y = R(x)yα; α= 0 ⇒ linear;α= 1
⇒ separable; otherwise, let v = y1-α ⇒ linear
Example: 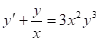
Higher Order Linear Ordinary Differential Equations
(i) Homogeneous Linear ODEs
An linear ordinary differential equation of order n is said to be homogeneous if it is of the form
an(x)y(n) + an - 1(x)y(n - 1) + .... + a1(x)y' + a0 (x)y = 0
where y'= dy/dx i.e., if all the terms are proportional to a derivative of y (or y itself) and there is no term that contains a function of x alone.
However, there is also another entirely different meaning for a first-order ordinary differential equation, such an equation is said to be homogeneous if it can be written in the form dy/dx = F(y/x).
(i) Homogeneous Linear ODEs with constant coefficients
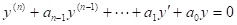 : Substituting y= eλx, we obtain the characteristic equation λn + an-1λn-1 + ...+ a1λ + a0 = 0.
: Substituting y= eλx, we obtain the characteristic equation λn + an-1λn-1 + ...+ a1λ + a0 = 0.
(a) Distinct real roots: The general solution is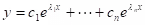
Example: y''' - 2y'' - y' + 2y =0.
Solution: y= c1e-x+ c2ex + c3e2x
(b) Simple complex roots: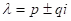 , y1 = epx cos(qx), y2 = epx sin(qx) .
, y1 = epx cos(qx), y2 = epx sin(qx) .
Example: y''' - y'' - 100y' + 100y =0.
Solution: y = c1ex + c2 cos10x + c3 sin10x.
(c) Multiple real roots: If λ is a real root of order m, then m corresponding linearly independent solutions are: eλx,xeλx, x2eλx,xm-1eλx
Example: y(5) - 3y(4) + 3y''' - y'' = 0.
Solution: y = c1 + c2x + (c3 + c4x + c5x2)ex.
(d) Multiple complex roots: If are complex double roots, the corresponding linearly independent solutions are:
are complex double roots, the corresponding linearly independent solutions are:
epx cos(qx), epx sin(qx),xepx cos(qx), xepx sin(qx), .- Convert the higher-order differential equation to a system of first-order equations.
Example: .
.
(ii) Non - Homogeneous Linear ODEs
- y(n) + pn-1(x)y(n-1) + ...+ p1(x)y' + p0(x)y = g(x) the general solution is of the form: y = yh + yp where yh is the homogeneous solution and yp is a particular solution.
- Method of undermined coefficients
Example: y'''+ 3y'' + 3y'+y = 30e
Solution: y = (c1 + c2x + c3x2)e-x + 5x3e-x
- Method of variation of parameters:
yp = u1y1 +...+ unyn
where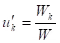 , k = 1,...., n.
, k = 1,...., n.
Example: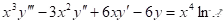 .
.
Solution: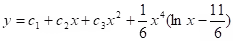 .
.
Points to Remember
- F(x,y,y', ....y(n)) = 0, a nth order ODE if the nth derivative
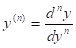 of the unknown function y(x) is the highest occurring derivative.
of the unknown function y(x) is the highest occurring derivative. - Linear ODE: y(n) + pn - 1(x)y(n - 1) + ...+ p1(x)y' + p0(x)y = g(x)
- Homogeneous linear ODE: y(n) + pn - 1(x)y(n - 1) + ...+ p1(x)y' + p0(x)y = g(x) = 0
Theorem: Fundamental Theorem for the Homogeneous Linear ODE: For a homogeneous linear ODE, sums and constant multiples of solutions on some open interval I are again solutions on I. (This does not hold for a nonhomogeneous or nonlinear ODE!).
General solution: y= c1y1+...+ cnyn, where y1,....,yn is a basis (or fundamental system) of solutions on I; that is, these solutions are linearly independent on I. - Linear independence and dependence: n functions y1,....,yn are called linearly independent on some interval I where they are defined if the equation k1y1,....,knyn = 0 on I implies that all k1,....,kn are zero. These functions are called linearly dependent on I if this equation also holds on I for some k1,....,kn not all zero.
Example: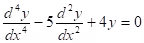 . Sol.: y = c1e-2x + c2e-x + c3ex + c4e2x
. Sol.: y = c1e-2x + c2e-x + c3ex + c4e2x
Theorem: Let the homogeneous linear ODE have continuous coefficients p0(x),... , pn-1(x) on an open interval I. Then n solutions y1,....,yn on I are linearly dependent on I if and only if their Wronskian is zero for some x= x0 in I. Furthermore, if W is zero for x= x0, then W is identically zero on I. Hence if there is an in I at which W is not zero, then y1,....,yn are linearly independent on I, so that they form a basis of solutions of the homogeneous linear ODE on I.
in I at which W is not zero, then y1,....,yn are linearly independent on I, so that they form a basis of solutions of the homogeneous linear ODE on I.
Wronskian: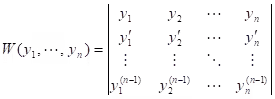
- Initial value problem: An ODE with n initial conditions y(x0) =K0, y'(x0) = K1, yn-1(x0) = Kn .
Example 1. Determine the order and degree of 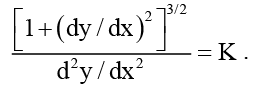
Solution: The given differential equation when written as a polynomial in derivatives becomes
The highest order differential coefficient in this equation is 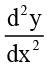 and its power is 2.
and its power is 2.
The order is 2 and degree is 2.
Example 2. Solve dy/dx = (x + y + 1)2, if y(0) =0
Solution: Putting x + y + 1 = t, we get 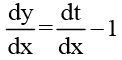
Thus, the given equation becomes 
Thus, the given equation becomes 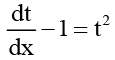 or
or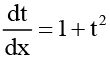
Integrating both side, we get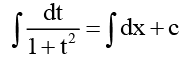
or tan-1 t = x + c ⇒ tan-1(x + y + 1) = x + c
⇒ x + y + 1 = tan (x + c) When x = 0, y = 0 1 = tan (c)
⇒ c = p/4
Thus, the solution is given by x + y + 1 tan (x + p/4).
Example 3. Solve the differential equation (x2 – y2) dx + 2xy dy = 0, given that y = 1 when x = 1
Solution: We have (x2 – y2)dx + 2xy dy = 0
(x2 – y2)dx = - 2xydy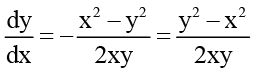 ...(i)
...(i)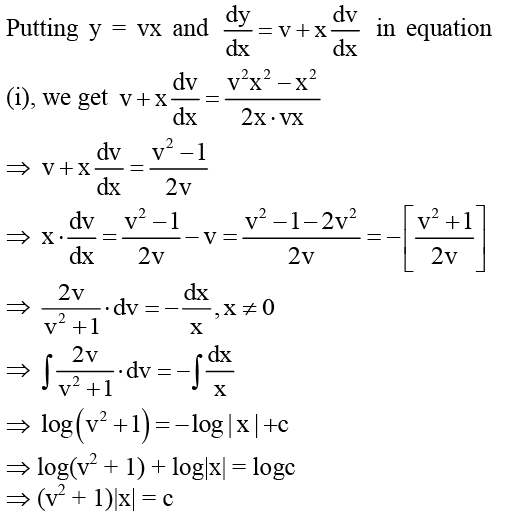
⇒ log ( v2 + 1) = - log | x | +c
⇒ log(v2 + 1) + log|x| = logc
⇒ (v2 + 1)|x| = c
Now putting v = y/x
(y2/x2 + 1)|x| = c
⇒ (x2 + y2) = c|x|
Substituting x = 1 and y = 1, we get
c =2
Putting value of c = 2 in equation (2), we get
x2 + y2 = 2x or x2 + y2 = 2(-x).
Hence, x2 + y2 = 2x is the required solution.
|
65 videos|129 docs|94 tests
|
FAQs on Differential Equations - Engineering Mathematics - Engineering Mathematics
| 1. What is the order of a differential equation? |  |
| 2. What is the degree of a differential equation? |  |
| 3. What is a separable differential equation? |  |
| 4. What are linear differential equations? |  |
| 5. What are exact differential equations? |  |

















