Differential Equations | Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE) PDF Download
Q1: A partial differential equation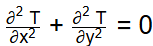
is defined for the two-dimensional field T : T(x, y), inside a planar square domain of size 2 m × 2 m. Three boundary edges of the square domain are maintained at value T = 50, whereas the fourth boundary edge is maintained at T = 100. The value of T at the center of the domain is [2024, Set-II]
(a) 50
(b) 62.5
(c) 75
(d) 87.5
Ans: (b)
Q2: For the following partial differential equation.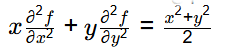
Which of the following option(s) is/are CORRECT? [2024, Set-I]
(a) elliptic for x>0 and y > 0
(b) parabolic for x > 0 and y > 0
(c) elliptic for x = 0 and y > 0
(d) hyperbolic for x < 0 and y > 0
Ans: (a,d)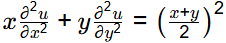
Q3: A5 cm long metal rod AB with initially at a uniform temperature of T0∘C. Thereafter, temperature at both the ends are maintained at 0∘C. Neglecting the heat transfer from the lateral surface of the rod, the heat transfer in the rod is governed by the one-dimensional diffusion equation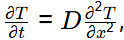 where D is the thermal diffusively of the metal, given as 1.0 cm2/s.
where D is the thermal diffusively of the metal, given as 1.0 cm2/s.
The temperature distribution in the rod is obtained as 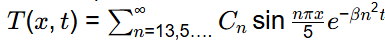 where x is in c m cm measured from A to B with x = 0 at A, t is s, Cn are constants in ∘C, T is in ∘C and β is in s−1.
where x is in c m cm measured from A to B with x = 0 at A, t is s, Cn are constants in ∘C, T is in ∘C and β is in s−1.
The value of β (in s−1 , rounded off to three decimal places) is ___ [2023, Set-II]
Ans: 0.394 to 0.396
Given: Diffusion equation: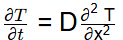
And also,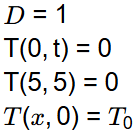
We know, solution of equation is given by,
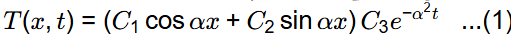
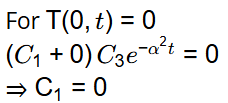
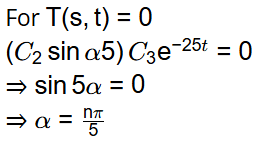
Now, from equation (1)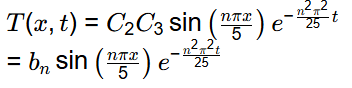
Generalize solution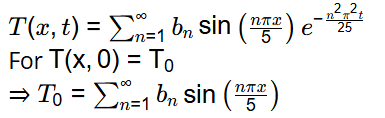
From fourier series,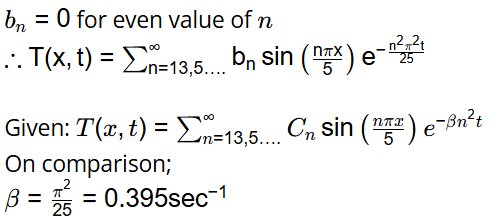
Q4: The steady-state temperature distribution in a square plate ABCD is governed by the 2-dimensional Laplace equation. The side AB is kept at a temperature of 100∘C and the other three sides are kept at a temperature of 0∘C. Ignoring the effect of discontinuities in the boundary conditions at the corners, the steady-state temperature at the center of the plate is obtained as 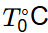 . Due to symmetry, the steady-state temperature at the center will be same (T0∘C), when any one side of the square is kept at a temperature of 100∘C and the remaining three sides are kept at a temperature of 0∘C. Using the principle of superposition, the value of T0 is ___ (rounded off to two decimal places). [2023, Set-II]
. Due to symmetry, the steady-state temperature at the center will be same (T0∘C), when any one side of the square is kept at a temperature of 100∘C and the remaining three sides are kept at a temperature of 0∘C. Using the principle of superposition, the value of T0 is ___ (rounded off to two decimal places). [2023, Set-II]
Ans: 24.9 to 25.1
We know, Laplace equation in two dimensional on a unit square with Dirichlet boundary condition: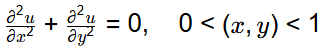
This Laplace equation is called harmonic function. Solution of Laplace equation,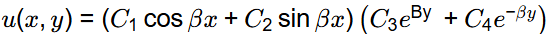
Let square ABCD is unit square.
Now, given
u(x, 0) = 0
u(0, y) = 0
u(1, y) = 0
u(x, 1) = 100 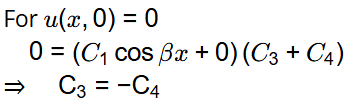
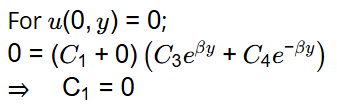
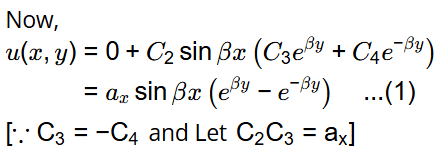

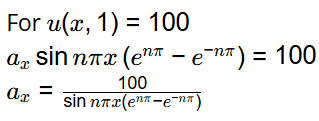
From eqn. (1), we get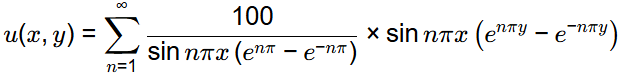
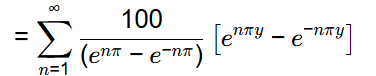
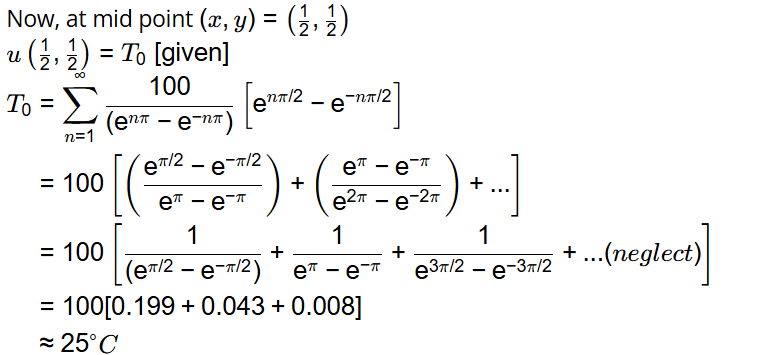
Q5: An ordinary differential equation is given below.
The solution for the above equation is
(Note: K denotes a constant in the options) [2019 : 2 Marks, Set-II]
(a) y = Kxex
(b) y = Kxe-x
(c) y = Klnx
(d) y = Kxlnx
Ans: (c)
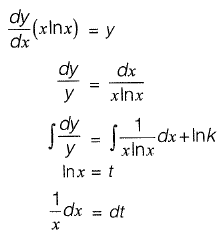
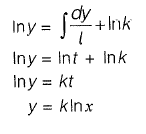
Q6: Consider the ordinary differential equation  Given the values of y(1) = 0 and y(2) = 2, the value of y{3) (round off to 1 decimal place), is_______ [2019 : 2 Marks, Set-I]
Given the values of y(1) = 0 and y(2) = 2, the value of y{3) (round off to 1 decimal place), is_______ [2019 : 2 Marks, Set-I]
Ans: y{3} = (6)
Q7: A one-dimensionai domain is discretized into N sub-domains of width Δx with node numbers i = 0,1,2, 3 ....... N. If the time scale is discretized in steps of Δt, the forward-time and centered- space finite difference approximation at nth node and time step, for the partial differential equation 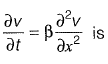
(a) 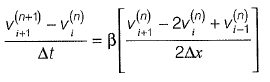
(b) 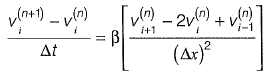
(c) 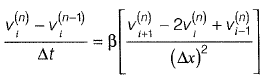
(d) 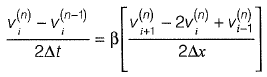 [2019 : 2 Marks, Set-I]
[2019 : 2 Marks, Set-I]
Ans: (b)

Approximate time derivative in equation (i) with forward difference,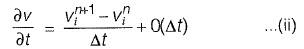
Note that the right hand side only in value v at x = xi
Use the central difference approximation to 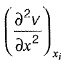 and evaluate all the terms at time n.
and evaluate all the terms at time n.
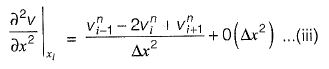
Substituting equation (ii) in the left hand side of equation (i), substitute the equation (iii) into the right hand side of equation (i), and collect the truncation error terms to get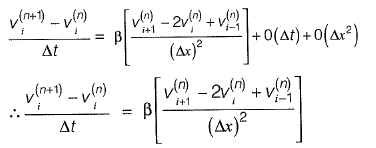
Q8: The solution of the equation 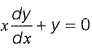 passing through the point (1,1) is
passing through the point (1,1) is
(a) x
(b) x2
(c) x-1
(d) x-2 [2018 : 1 Mark, Set-II]
Ans: (c)
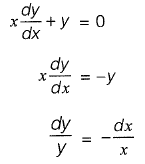
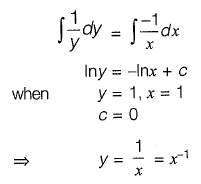
Q9: The solution (up to three decimal places) at x = 1 of the differential equation 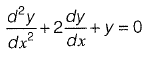 subject to boundary conditions y(0) = 1 and
subject to boundary conditions y(0) = 1 and
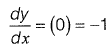 [2018 : 2 Marks, Set-I]
[2018 : 2 Marks, Set-I]
Ans: 0.368
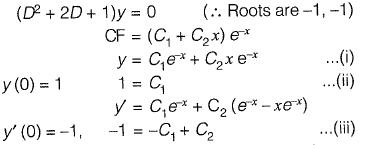
From eq. (ii) and (iii),
Q10: Consider the following second-order differential equation:
y "- 4y' + 3 y = 2t - 3t2
The particular solution of the differential equation is
(a) - 2 - 2t - t2
(b) - 2t - t2
(c) 2t - t2
(d) - 2 - 2t - 3t2 [2017 : 2 Marks, Set-II]
Ans: (a)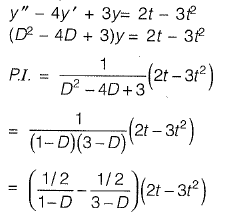
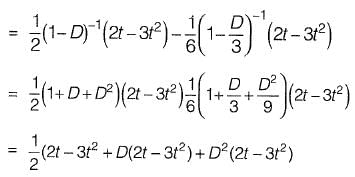
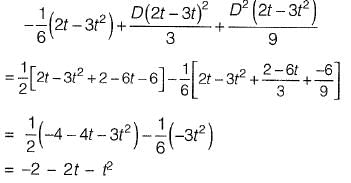
Q11: The solution of the equation 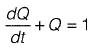 with Q = 0 at t = 0 is
with Q = 0 at t = 0 is
(a) Q(t) = e-t - 1
(b) Q(t) = 1 + e-t
(c) Q(t) = 1 - et
(d) Q(f) = 1 - e-t [2017 : 2 Marks, Set-I]
Ans : (d)
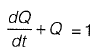
comparing with standard form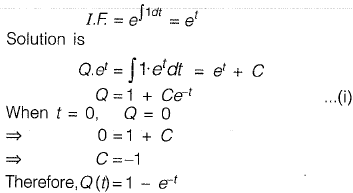
Q12: Consider the following partial differential equation: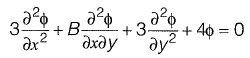
For this equation to be classified as parabolic, the value of B2 must be ________ . [2017 : 1 Mark, Set-I]
Ans: 36
Given that the partial differential equation is parabolic.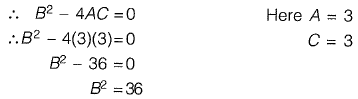
Q13: The respective expressions for complimentary function and particular integral part of the solution of the differential equation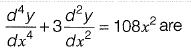
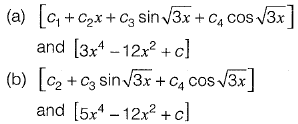
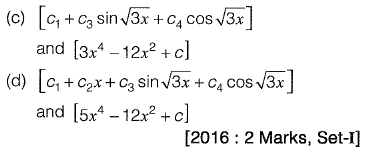
Ans: a
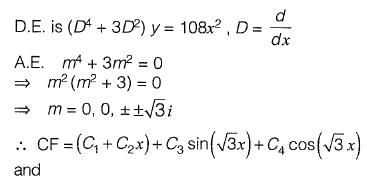
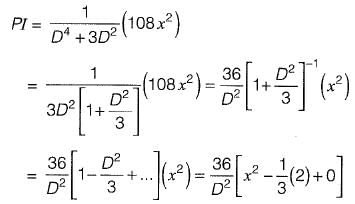

Q14: The solution of the partial differential equation 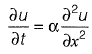 is of the form
is of the form 
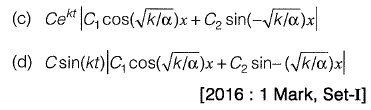
Ans: (b)
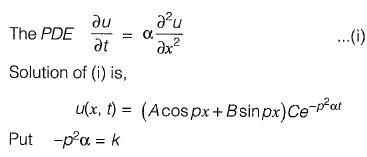
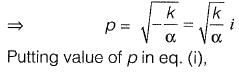
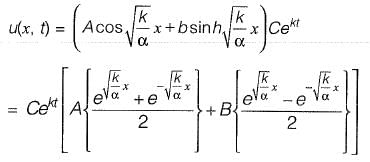
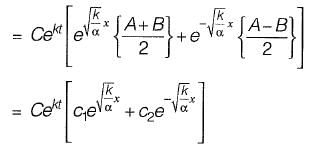
Q15: The type of partial differential equation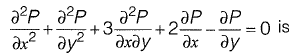
(a) elliptic
(b) parabolic
(c) hyperbolic
(d) none of these [2016 : 1 Mark, Set-I]
Ans: (c)
Comparing the given equation with the general form of second order partial differential equation, we have A = t , B = 3, C = 1
=> B2 - 4AC = 5 > 0
∴ PDE is Hyperbola.
Q16: Consider the following second order linear differential equation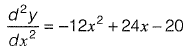
The boundary conditions are: at x = 0, y = 5 and x = 2, y = 21
The value of y at x = 1 is . [2015 : 2 Marks, Set-II]
Ans: y = 18
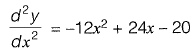
Integrating both sides wrt. x,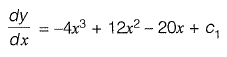
Integrating both sides wrt. x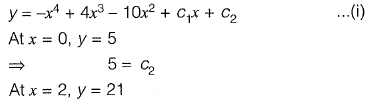

Q17: Consider the following difference equation
Which of the following is the solution of the above equation (c is an arbitrary constant)? [2015 : 2 Marks, Set-I]
(a) 
(b) 
(c) 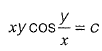
(d) 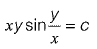
Ans: c
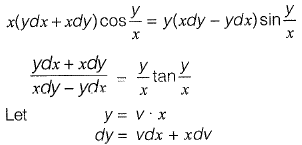
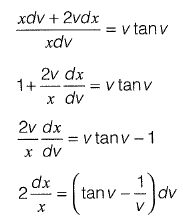
Integrating both side
Q18: The integrating factor for differential equation 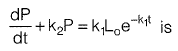 [2014 : 1 Mark, Set-II]
[2014 : 1 Mark, Set-II]
(a) 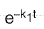
(b) 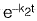
(c) 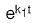
(d) 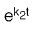
Ans: (d)
Q19: The solution of the ordinary differential equation 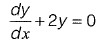 for the boundary condition, y = 5 at x = 1 is [2011 : 2 Marks]
for the boundary condition, y = 5 at x = 1 is [2011 : 2 Marks]
(a) y = e-2x
(b) y = 2e-2x
(c) y = 10.95 e-2x
(d) y = 36.95 e-2x
Ans: (d)
Given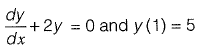
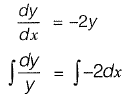
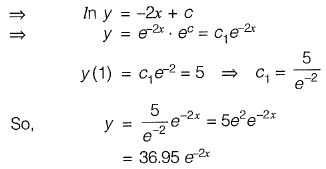
Q20: The solution of the diffrential equation 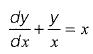 with the condition that y = 1 at x = 1 is [2011 : 2 Marks
with the condition that y = 1 at x = 1 is [2011 : 2 Marks
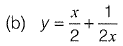
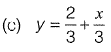
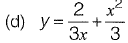
Ans: (d)
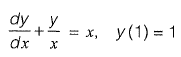
This is a linear differential equation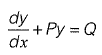
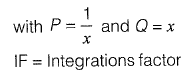
solution is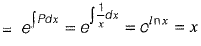
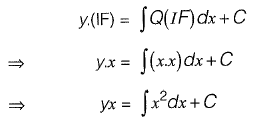
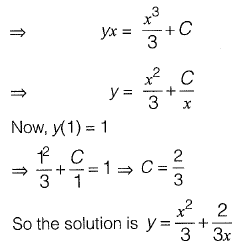
Q21: A parabolic cable is held between two supports at the same level. The horizontal span between the supports is L. The sag at the mid-span is h. The equation of the parabola is 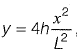 where x is the horizontal coordinate and y is the vertical coordinate with the origin at the centre of the cable. The expression for the total length of the cable is
where x is the horizontal coordinate and y is the vertical coordinate with the origin at the centre of the cable. The expression for the total length of the cable is
[2010 : 2 Marks]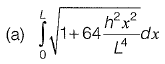
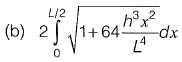
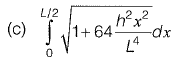
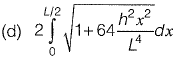
Ans: (d)
Length of curve f(x) between x = a and x = b is given by,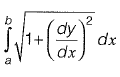

since, y = 0 at x= 0
and y = h at x = L/2
(As can be seen from equation (i), by substituting x = 0 and x = L/2)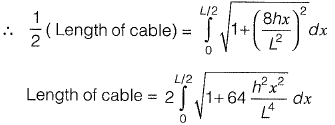
Q22: The partial differential equation that can be formed from z = ax + by + ab has the form (with 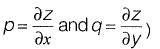 [2010 : 2 Marks]
[2010 : 2 Marks]
(a) z = px + qy
(b) z = px + pq
(c) z = px + qy + pq
(d) z = qy + pq
Ans: (c)
z = a x + b y + a b ...(i)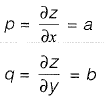
Substituting a and b in (i) in terms of p and q, we get,
z = px + qy + pq
Q23: The solution to the ordinary differential equation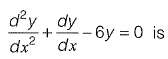 [2010 : 2 Marks]
[2010 : 2 Marks]
(a) y= c1e3x + c2e-2x
(b) y= c1e3x + c2e2x
(c) y= c1e-3x + c2e2x
(d) y= c1e-3x + c2e-2x
Ans: (c)
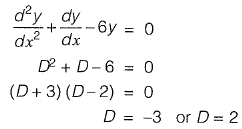
∴ Solution is y = = c1e-3x + c2e2x
Q24: The order and degree of the differential equation 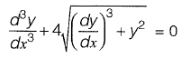 are respectively [2010 : 1 Mark]
are respectively [2010 : 1 Mark]
(a) 3 and 2
(b) 2 and 3
(c) 3 and 3
(d) 3 and 1
Ans (a)
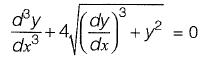
Removing radicals we get,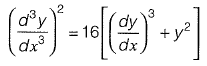
∴ The order is 3 since highest differential is 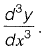
The degree is 2 since power of highest differential is 2.
FAQs on Differential Equations - Topic wise GATE Past Year Papers for Civil Engineering - Civil Engineering (CE)
| 1. What are differential equations and why are they important? |  |
| 2. What are the main types of differential equations? |  |
| 3. How do you solve a first-order ordinary differential equation? |  |
| 4. What is the significance of initial conditions in solving differential equations? |  |
| 5. Can differential equations be solved using numerical methods? |  |
















