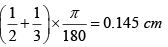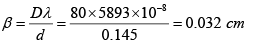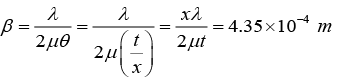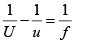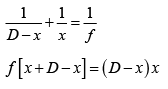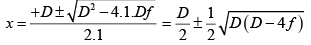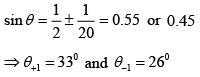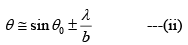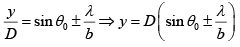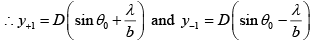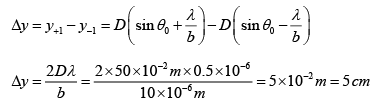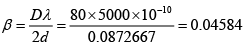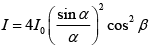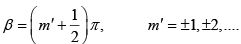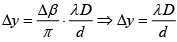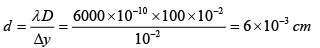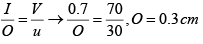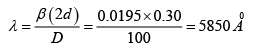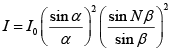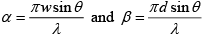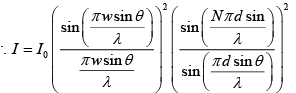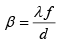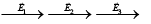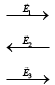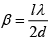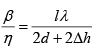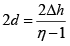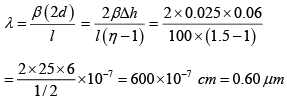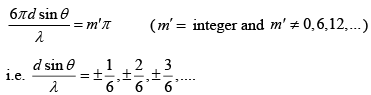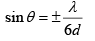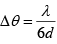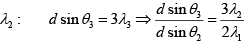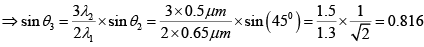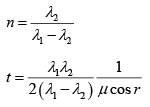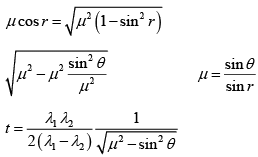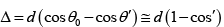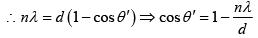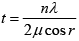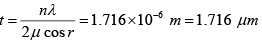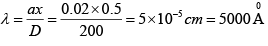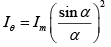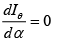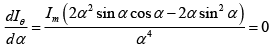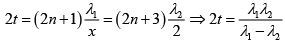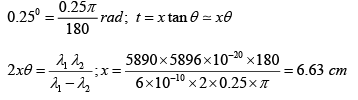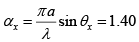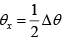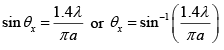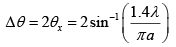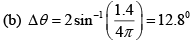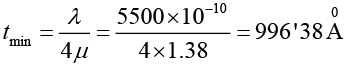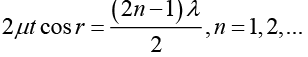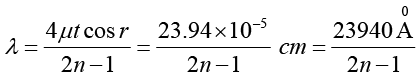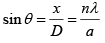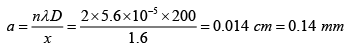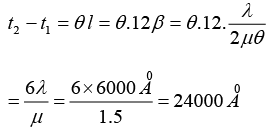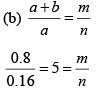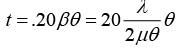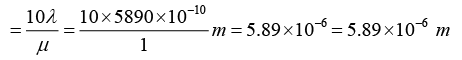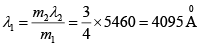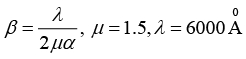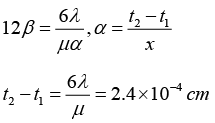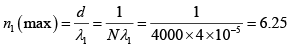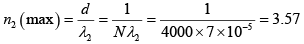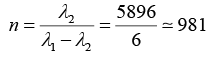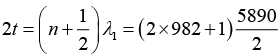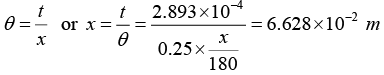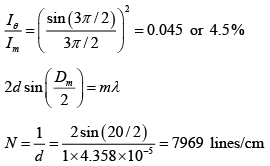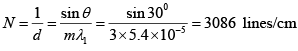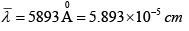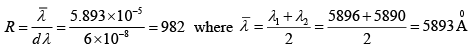Diffraction of Light: Assignment | Oscillations, Waves & Optics - Physics PDF Download
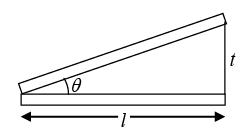
Q.1. Interference fringes are produced using a sodium light (λ = 5893 Å) and a biprism of refractive index 1.5 and refracting (1/2)0 and (1/3)0. The distance of the screen from the biprism is 60 cm and from the source is 80 cm . Find the separation of the two virtual sources and fringe width.
d = a(μ - 1)(α1 + α2) = 20(1.5 - 1)
Q.2. Monochromatic light emitted by board source of wavelength 5800Å falls normally on two plates of glass enclosing a wedge shaped film. The plates touch at one end and are separated at a point 12 cm from that end by a wire of 0.08 cm. Find the fringe width.
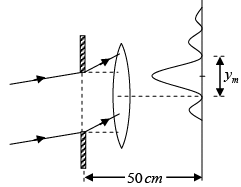
Q.3. Show that the distance between the source and the screen should be greater than 4f one wants two positions of convex lens (of focal length f ) to obtain the images of virtual sources on the screen in a Fresnel Biprism experiment.
u = -x
U = D - x
∴ D > 4f to obtain two values of x.
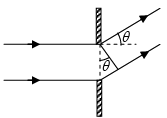
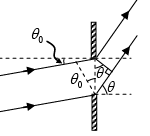
Q.4. Light with wavelength λ = 0.50μm falls on a slit of width b = 10 μm at an angle 300 to its normal. Find the angular position of the first minima located on both sides of the central Fraunhofer maxima. Also calculate the width of the central maxima, if screen is placed at 50 cm from slit.
The relation b sinθ =mλ for minima (when light is incident normally on the slit) has a simple interpretation: b sinθ is the path difference between extreme wave normal emitted at an angle θ.
When light is incident at angle θ0, the path difference is p.d . = b sinθ - b sinθ0 and the condition of minima is b (sinθ - sinθ0) = mλ
For the first minima b (sinθ - sinθ0) = ±λ or sinθ = sinθ0 ± (λ/b)
Putting the numbers θ0 = 300, λ = 0.50μm, b = 10μm
Let ym is the minima position on the screen
∴ tanθ = y/D
For small angle of diffraction
tanθ = θ/D
∴ θ = y/D ...(i)also sinθ = sinθ0 ± (λ/b) and for small angle
From (i) and (ii)
The width of the central maxima is
Q.5. In a biprism experiment the obtuse angle of the prism is 1780 and one of the acute angle is 0.750. The refractive index of the biprism is μ= 1.5. If the distance of slit to biprism is 5 cm and biprism to screen is 75 cm, then what is the fringe width for the light of wavelength 5890Å.
2d =a (μ -1) (α1 + α2) = 5(1.5 - 1) x 20 x 3.14/1800 = 0.087266
Q.6. A plane wave of light from a laser has a wavelength of 6000Å. The light is incident on a double slit. After passing through the double slit, the light falls on a screen 100cm beyond the double slit. The intensity distribution of the interference pattern on the screen is shown
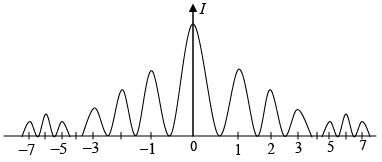
What is the width of each slit and what is the separation of the two slits?
For double slit interference
whereb being the width of each slit, d the separation of their centers, D the distance between the screen and the double slits.
The minima are given by
Thus the fringe spacing Δy is given by
Hence, for Δy = 1cm
The pattern shows the missing order d/b = 4, from which we get the width of each slit.
b = d/4 = 1.5 x 10-3cm
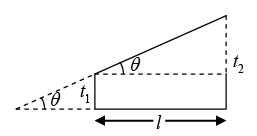
Q.7. In a biprism experiment with sodium light, bands of width 0.0195 cm are observed at 100 cm from the slit on introducing a convex lens 30 cm away from the slit, two images of the slit are seen 0.7 cm apart, at 100 cm distance from the slit. What is the wavelength of light?
β = 0.0195 cm,
D = 100 cm,
u = 30 cm
D = a + b = 100cm,
v = 70cm
For convex lens
Q.8. The diffraction pattern given in figure below is produced on a screen by light passing through three distance slits of width w and spacing d.
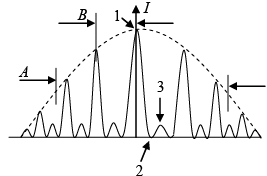 How will the envelop width A and the separation of the peaks B change if:
How will the envelop width A and the separation of the peaks B change if:
(a) the slit width w is increased
(b) the slit spacing d is increased
(c) the wavelength of the light is increased
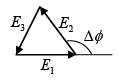
(d) draw phasor vector diagram of E -field at point 1, 2 and 3
The light intensity distribution on the screen is represented by
where
where N = 3, sinθ ≅4/f where f is the focal length of a lens placed behind the slits. From the formula, we get the width of the envelopsand the separation of the peaks i.e. fringe width
(a) A decreases and B remains unchanged when w is increased
(b) A remain unchanged but B decreases when d is increased
(c) Both A and B will increase when the wavelength of the light is increased
(d) the amplitude of the E - field arriving at point 2 on the screen are represented by three equal vectors summed with the appropriate phases for this position. They add to zero, which is why there is zero intensity at this point on the screen
The vector diagram for point 1 is
The vector diagrams for point 3 is
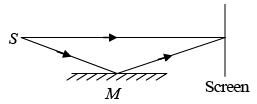
Q.9. In Lloyd’s mirror experiment, a light wave emitted directly by the source (narrow slit) interferes with the wave reflected from a mirror M . As a result, an interference fringe pattern is formed on the screen. The source and the screen are separated by a distance l = 100 cm . At a certain position of the source, the fringe width on the screen is 0.25 mm and after the source was moved away from the mirror plane by Δh= 0.6mm , the fringe width is decreases by β = 1.5 times. Find the wavelength of light.

η(2d) = 2d + 2Δh
Q.10. A plane light wave of wavelength λ is incident on a grating consisting of 6 identical parallel slits a distance d apart.
(a) At what angles with the normal are the interference maxima?
(b) What is the angular width of the interference maxima, say from the maximum to the nearest null?
(c) What is the ratio of the intensity at an interference maximum to the intensity obtained for a single slit?
(d) Sketch the interference pattern as a function of angle.
The intensity distribution for Fraunhofer diffraction is given by
where N is the number of slits (in this case N = 6)
(a) The interference maxima occur when
i.e. sinθ = nλ/d
(b) Minima of zero intensity occurs when
For central maxima
∴ Half angular width of central maxima is
(c) I(0) = N2I0= 36I0
(d) The intensity distribution as a function of angle is
Q.11. A parallel beam of light of wavelength λ is incident normally on a thin polymer film with air on both sides. If the film has a refractive index n > 1 , then second order bright fringes can be observed in reflection. Find the thickness of the film.
2nt = (2m + 1)λ/2
m = 1
t = 3λ/4n
Q.12. With light falling normally on a diffraction grating, the angle of diffraction of second order is equal to 450 for a wavelength λ1 = 0.65μm. Find the angle of diffraction of third order for a wavelength λ2 = 0.5μm.
d sinθ = nλ
For λ1 : d sinθ2 = 2λ1
For
∴ θ3 = sin-1(0.816) ≅ 550
Q.13. A soap film of refractive index μ is illuminated with white light incident at an angle θ. The light reflected by it is examined and two dark bands are focussed corresponding to wavelengths λ1 and λ2. What is the thickness of the film?
2μtcosr = nλ1 = (n + 1)λ2
Q.14. A laser beam λ = 6.3 x 10-3 cm is directed as grazing angle θ0 onto a steel ruler which is calibrates in 1/16 inch. The light reflects from the surface of the ruler and is projected onto a vertical wall 10 m away.
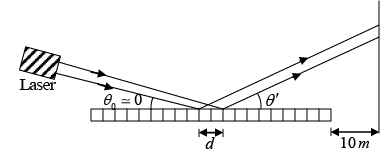 (a) Drive the condition on θ' for interference maxima on the wall. Assume for simplicity that the laser beam is initially almost parallel to the ruler surface (i.e. θ0 ≥ 0)
(a) Drive the condition on θ' for interference maxima on the wall. Assume for simplicity that the laser beam is initially almost parallel to the ruler surface (i.e. θ0 ≥ 0)
(b) What is the vertical separation on the wall of the zeroth and first order spots of the pattern?
The optical path difference of the parallel light rays is
The interference maxima occur when Δ = nλ ( n = 0,1, 2, .... )
(b) When n = 0, θ' = 0
when n = 1, θ' = 1 - (λ/d) = 0.9996
Taking d = 1 division(1/16(inch))
The vertical separation on the wall between the zeroth and the first order spats is y = D . tanθ'1= 0.28m
Q.15. A parallel beam of light (λ = 5890Å) strike a film of oil (μ = 1.46). If the 8th dark fringe be seen when viewed at an angle of 300 to the normal, then what is the thickness of the film.
2μt cos r = nλ
n = 8
λ = 5890 x 10-10m
μ = 1.46
i = 300
sin i/sin r = r
cos r = 0.94
Q.16. In Fraunhofer diffraction due to a narrow slit a screen is placed 2 m away from the lens to obtain the pattern. If the slit width is 0.2 mm and the first minima are 5 mm on either side of the central maximum, find the wavelength of light.
a sinθ = mλ (i)
(ii)
If D is the slit screen distance and x the distance of the first minimum from the central maximum, then tanθ ≈ sinθ = x/D (iii)
combining (ii) and (iii)
Q.17. A thin soap film (μ = 1.33) is illuminated by white light at an angle of incidence i = sin(4/5). In reflected light two dark consecutive fringes are observed for wavelengths λ1 = 6100Å and λ2 = 6000Å. Calculate the thickness of the film.
nλ1 = (n+1)λ2
n = 60
sin i = 4/5
μ = 4/3
cos r = 0.8
2 μt cos r = nλ,
Q.18. The intensity Iθ for the single-slit diffraction pattern is given by Iθ = Im (sinα/α)2, where α = (πa/λ)sinθ and Im is the intensity of the central maximum. Show that the intensity maxima can be found out from the condition, tanα = α.
Differentiating Iθ with respect to α and setting
∴ 2α sinα (α cos α - sin α) = 0
∴ tan α = α
Q.19. Interference pattern in reflected light for normal incidence on a wedge shaped air film is seen using bichromatic (λ1 = 5896 Å, λ2 = 5890Å) source of light. The angle of wedge is 0.250 of arc. Find out the minimum distance from the edge of the wedge at which the maximum due to each wavelength coincides.
Q.20. (a) Obtain the expression for Δθ, the half-width at half central maximum of single-slit Fraunhofer diffraction.
(b) Calculate Δθ for a/λ = 4
The half-width is the angle between the two points in the pattern where the intensity is one-half the centre of the pattern:
...(i)
The solution of (i) found by numerical method is αx = 1.40 rad
where
or
Q.21. A surface of refractive index 1.52 is to be coated with a film of refractive index 1.38 to minimize the reflection. Determine the minimum thickness of film for normal incidence of light of wavelength 5500Å.
Q.22. A beam of light contains a mixture of wavelength λ1 and λ2. When the light is incident on a single slit the diffraction minimum of λ1 coincides with the second minimum of λ2. How are the two wavelengths related?
a sinθ = mλ
a sinθ1 = 1.λ1
a sinθ2 = 2λ2
But θ1 = θ2
∴ λ1 = 2λ2
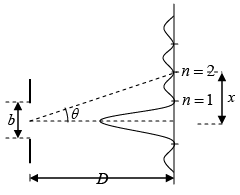
Q.23. A soap film (μ = 1.33) of thickness 5 x 10-5 cm is viewed at an angle 350 to the normal. Find the wavelengths of light in the visible spectrum (a) which will be absent from the reflected light, (b) will be strongly reflected.
μ = sin i/sin r, cos r = 0.90, t = 5 x 10-5cm
(a) 2μt + cos r = nλ
n = 1 λ1 = 12000Å, n = 2 λ2 = 6000Å
n = 3 λ3 = 4000Å, n = 4 λ4 = 3000Å,(b)
n = 0, λ1 = 23, 940 Å → IR
n = 1, λ2 = 7980 Å
n = 2, λ3 = 4788 Å → Visible
n = 3, λ4 = 3420 Å
n = 4, λ5 = 2660 Å → UV
Q.24. A single slit is illuminated normally by a monochromatic light of wavelength of 5600Å and diffraction bands are observed on a screen 2 m away. If the centre of the second dark band is 1.6 cm from the central bright band, deduce the slit width.
∴
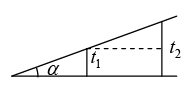
Q.25. A square piece of cellophane film with refractive index 1.5 has a wedge section with thickness at two opposite sides as t1 and t2. If by using the light of wavelength λ = 6000Å, the number of fringes appearing in the film is 12, calculate the difference (t2 -t1). Consider the condition of normal incidence of light and very small wedge angle.
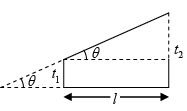
l = 12β
Q.26. (a) What are missing orders in the double-slit diffraction pattern? Explain.
(b) Deduce the missing order for a double-slit diffraction pattern, if the slit widths are 0.16 mm and they are 0.8 mm apart.
Let m be the order of interference. If the slit width a is maintained constant and the separation of the slits d is varied, the scale of the interference pattern varies, but that of the diffraction pattern remains unchanged. If the diffraction angle corresponds to the minimum given by (i) then a particular order of interference maxima may be absent. This is called a missing order. Thus, a missing order is realized for an angle q for which the following two equations are simultaneously satisfied:
d sinθ = mλ (m = 1, 2, 3, ....) (i)
a sinθ = nλ (n = 1, 2, 3, ....) (ii)
Dividing (i) by (ii)(iii)
since m and n are both integers, missing orders will occur when d /a is in the ratio of two integers. Expressing d as the sum of the slit width a and the opaque space b between consecutive slits, that is
d = a+ b (iv)
(iii) can be written as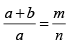
In particular, ifIn this case the first-order spectrum will be absent and the resultant diffraction pattern will be similar to that of a single slit.
Ifthat is the width of the slit is equal to the width of the opaque space.
Here the second-order spectrum will be absent.
The above relation is satisfied for
n = 1, 2, 3, ...
m = 5,10,15, ...
Thus the order 5,10,15, etc. of the interference maxima will be missing, in the diffraction pattern.
Q.27. Two plane glass surface in contact along one edge are separated at the opposite edge by a thin wire. If 20 interference fringes are observed between these edges in sodium light (λ = 5890Å) of normal incidence, what is the thickness of the wire.
Q.28. In a grating spectrum which spectral line in the fourth order will overlap with the third order of 5400Å?
m1λ1 =m2λ2
Q.29. A square pieces of cellophone film with refractive index 1.5 has a wedge section so that its thickness at two opposite sides is t1 and t2. If by using the light of wavelength λ = 6000Å, the number of fringes appearing in the film is 12, calculate the difference t2 - t1.
Q.30. How many orders will be observed by a grating having 4000 lines/cm, if a visible light in the range 4000-7000Å is incident normally?
The maximum order of spectrum varies between 3 (towards red) and 6 (towards violet).
Q.31. If the angle of wedge is 0.25o and wavelengths of sodium lines are 5890 Å and 5896Å. Find the minimum distance from the apex at which the maximum due to two wavelengths coincides when observed in the reflected light.
θ = 0.250, λ = 5890Å and λ = 5896Å
for max intensity due to λ1
for max intensity due to λ2
For air film
t = 2.893 x 10-4m
x = 6.628 x 10-2
Q.32. Show that in a grating if the opaque and the transparent strips are of equal width then all the even orders, except m = 0 , will be missing.
(condition for missing orders)
∴ m = 2n
The above condition is satisfied for
n = 1, 2, 3, ...
m = 2, 4, 6, ...
Thus all the even orders of interference fringes (2, 4, 6, ...), except m = 0 , are missing.
Q.33. Show that the intensity of the first secondary maxima relative to that of central maxima in the single-silt diffraction is about 4.5%.
The secondary maxima lie approximately halfway between the minima. Now, the intensity at an angle θ is given by
(i)
where(ii)
Minima occur in (i) when
α = mπ (m = 1, 2, 3, ...) (iii)
Therefore the first secondary maximum would occur halfway between first minimum and second minimum. Therefore,(iv)
Substituting (iv) into (i)
Q.34. A diffraction grating used at normal incidence gives a green line, λ = 5400Å in a certain order superimposed on the violet line, λ = 4050Å of the next higher order. If the angle of diffraction is 300, how many lines are there per centimeter in the grating?
Condition for overlapping is
mλ1 = (m+ 1)λ2
5400m = 4050 x (m + 1)
∴ m = 3
d sinθ = mλ1
Q.35. Calculate the least width that a grating must have to resolve the components of D lines (5890 and 5896Å) in the second order. The grating has 800 lines/cm.
Δλ = λ1 - λ2 = 5896 - 5890 = 6 Å = 6 x 10-8 cm
Resolving power
R = Nm(Total number of lines)
If N' is the number of lines/cm, then the width of the grating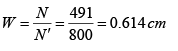
|
54 videos|22 docs|14 tests
|
FAQs on Diffraction of Light: Assignment - Oscillations, Waves & Optics - Physics
| 1. What is diffraction of light? |  |
| 2. How does diffraction of light occur? |  |
| 3. What are the applications of diffraction of light? |  |
| 4. What is the significance of diffraction in understanding the nature of light? |  |
| 5. How does diffraction of light affect image formation? |  |