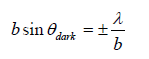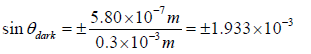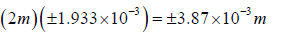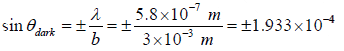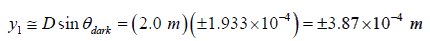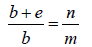Diffraction of Light | Oscillations, Waves & Optics - Physics PDF Download
Introduction
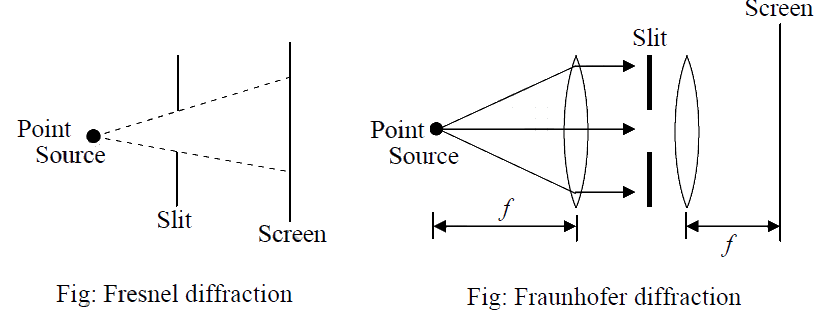
The spreading out of a wave when it passes through a narrow opening is usually referred to as diffraction, and the intensity distribution on the screen is known as the diffraction pattern.
The diffraction phenomena are usually divided into two categories: Fresnel diffraction and Fraunhofer diffraction.
In the Fresnel class of diffraction, the source of light and the screen are, in general, at a finite distance from the diffracting aperture. In the Fraunhofer class of diffraction, the source and the screen are at infinite distances from the aperture; this is easily achieved by placing the source on the focal plane of a convex lens and placing the screen on the focal plane of another convex lens. The two lenses effectively moved the source and the screen to infinity because the first lens makes the light beam parallel and the second lens effectively makes the screen receive a parallel beam of light.
Fraunhofer’s diffraction at a single slit
Let a parallel beam of monochromatic light of wavelength λ be incident normally upon a narrow slit of width AB = b placed perpendicular to the plane of the paper. Let the diffracted light be focused by a convex lens L on a screen XY placed in the focal plane of the lens. The diffraction pattern obtained on the screen consists of a central bright band, having alternative dark and weak bright bands of decreasing intensity on both sides.
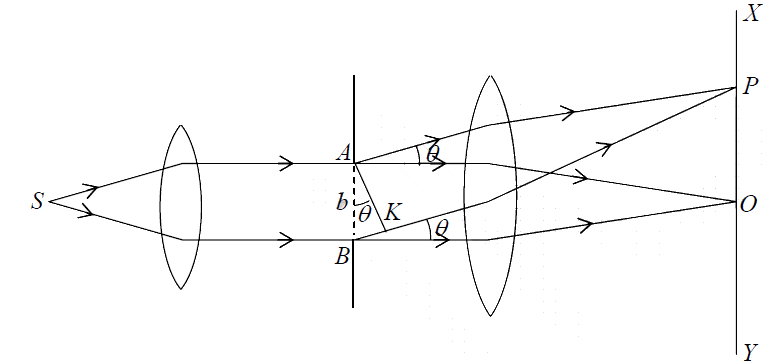
Explanation
In terms of wave theory, a plane wavefront is incident normally on the slit AB.
According to the Huygen’s principle, each point on AB sends out secondary wavelets in all directions. The rays proceeding in the same direction as the incident rays are focused at O, while those diffracted through an angleθ are focused at P . Let us find out the resultant intensity at P.
Let AK be the perpendicular to BK. As the optical path from the plane, AK to P are equal, the path difference between the wavelets from A to B in the direction
Path difference = BK = ABsinθ = bsinθ
The corresponding phase difference = 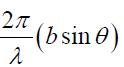
Let the width AB of the slit be divided into n equal parts. The amplitude of vibration at P . Due to the waves from each part will be the same, say equal to a. The phase difference between the waves from any two consecutive parts is 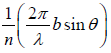 = δ(say).
= δ(say).
Hence the resultant amplitude at P is R
= 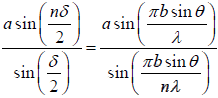
Let 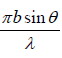 = α
= α
⇒ R = 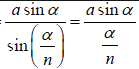
∵ α/n is small
R = 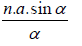
As n→∞, a→0 but the product na remains finite
Thus Resultant Amplitude at P due is R = 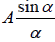 let na = A
let na = A
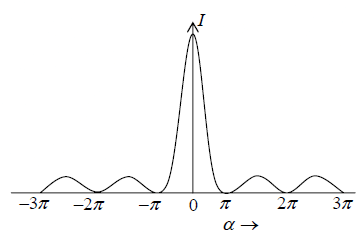
Thus resultant intensity at P ; I = R2 = 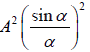
The constant of proportionality being taken as unity for simplicity
Condition for Maximum and Minimum intensity
Direction for Minimum Intensity
For minimum intensity I = 0 ⇒ 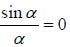 ⇒ sinα = 0 but α is not equal to zero.
⇒ sinα = 0 but α is not equal to zero.
Thus α = ±mπ where, m has an integral value1, 2, 3 except zero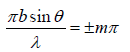
⇒ bsinθ = ±mλ, where m =1,2,3
Direction for Maximum Intensity
For direction of maximum intensity 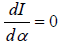
⇒ 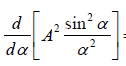 =0 ⇒
=0 ⇒ 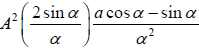 = 0
= 0
⇒ 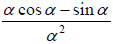 = 0
= 0
⇒ 2cosα − sinα = 0 ⇒ α = tanα
The equation is solved graphically by plotting the curve
y =α and y = tanα
the points of intersection give (approximately)
α = 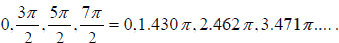
Substituting the value of α into the expression of I
The intensity of the central maxima I0 = 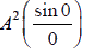 = A2
= A2
The intensity of the first maxima I1 = 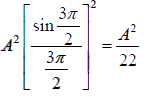
The intensity of the second maxima
I2 = 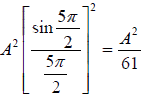
Thus the ratio of intensities of the successive maxima
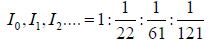
Clearly, most of the incident light is concentrated in the central maxima which occur in the direction α = 0 or 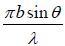 = 0
= 0
or θ = 0 i.e. in the same direction as the incident light
 Effect of Slit Width on Diffraction Pattern
Effect of Slit Width on Diffraction Pattern
If slit is made narrower
Since first minimum on either side of the central maximum occurs in the direction θ, given by equation bsinθ = ±λ
When the slit is narrowed (b is reduced), the angle θ increases which means the central maximum becomes wider. When the slit-width is as small as wavelength(b = λ ), the first minimum occurs atθ = 900, which means central maxima fills the whole space i.e. condition of uniform illumination.
Example 1: A monochromatic light with a wavelength of λ = 600nm passes through a single slit which has a width of 0.800mm.
(a) What is the distance between the slit and the screen be located if the first minimum in the diffraction pattern is at a distance 1.00mm from the center of the screen?
(b) Calculate the width of the central maximum.
(a) The general condition for destructive interference is
For smallθ , we employ the approximation sinθ ≈ tanθ = y/D which yields
The first minimum corresponds tom =1. If 1 y =1.00mm, then
L =
= 1.33m
(b) The width of the central maximum is W = 2y1 = 2 (1.00 x 10-3m) = 2.00mm
Example 2: A monochromatic light is incident on a single slit of width 0.800mm and a diffraction pattern is formed at a screen which is 0.800 m away from the slit. The second order bright fringe is at a distance 1.60mm from the centre of the central maximum. What is the wavelength of the incident light?
The general condition for destructive interference is
sinθ =
where small-angle approximation has been made.
Thus the position of the mth order dark fringe measured from the central axis is
ym =
Let the second bright fringe be located halfway between the second and the third dark
fringe. That is y2b =
The approximate wavelength of the incident light is then
λ =
= 6.40 x 10-7m
Example 3: Light of wavelength 580 nm is incident on a slit having a width of 0.30 mm. The viewing screen is 2 m from the slit. Find the positions of the first dark fringes and the width of the central bright fringe. What if the slit width is increased by an order of magnitude of 3.0 mm? What happens to the diffraction pattern?
To analyze the problem, note that the two dark fringes that flank the central bright fringe corresponds to
n = ±1.
∴
⇒
since, y1 = D tanθdark
For small angle θdark ≅ tanθdark ≅ sinθdark ≅ y1 / D
∴ y1 = D sinθdark =
The width of the central bright fringe is W = 2 |y1| = 2 × 3.87×10−3 m = 7.74 mm
Note that this value is much greater than the width of the slit.
We expect that angles at which the dark bands appear will decrease as b increases
Thus the diffraction pattern narrows.
For b = 3.0 mm, the sine of the angle θdark for the n = ±1 dark fringes are
∴
The width of the central bright fringe is
W = 2y1 = 2×3.87×10−4 m
⇒ W = 0.774 mm
Notice that this is smaller than the width of the slit
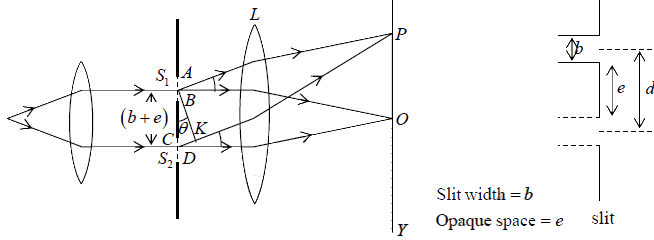
Fraunhofer’s Diffraction at a Double Slit
In Double Slit diffraction experiment, the pattern obtained on the screen is the diffraction pattern due to a single slit on which a system of interference fringes is superposed.
By Huygen’s principle every point in the slits AB and CD sends out secondary wavelets in all directions.
From the theory of diffraction at a single slit, the resultant amplitude due to wavelets diffracted from each slit in a direction θ is R = 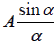 , where α =
, where α = 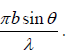
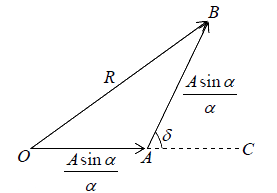
Consider the two slits as equivalent to two coherent sources placed at the middle points S1 and S2 of the slits and each sending wavelets of amplitude in a directionθ.
Consequently, the resultant amplitude at a point P on the screen will be the result of interference between two waves of same amplitude 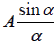 , and having a phase difference δ (say) and path difference S2K = (b + e) sinθ.
, and having a phase difference δ (say) and path difference S2K = (b + e) sinθ.
Phase difference δ = 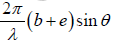
The resultant amplitude R
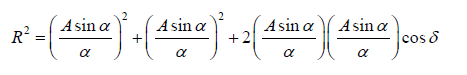
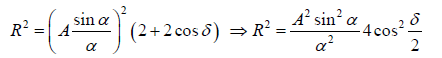
Let β = δ/2 ⇒ β = 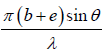
Therefore the resultant intensity at P is
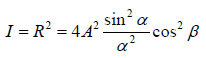
Thus the intensity in the resultant pattern depends on two factors
(i)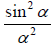 , which gives diffraction pattern due to each individual slit and
, which gives diffraction pattern due to each individual slit and
(ii) cos2 β, which gives interference pattern due to diffracted light waves from the two slits.
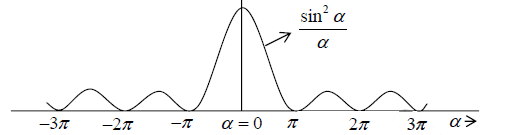
The diffraction term  gives central maximum in the directionθ = 0, having alternate minima and subsidiary maxima of decreasing intensity on either side the minima are obtained in the direction given by
gives central maximum in the directionθ = 0, having alternate minima and subsidiary maxima of decreasing intensity on either side the minima are obtained in the direction given by
sinα = 0
⇒ α = ±mπ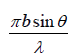 = ±mπ, where m =1,2,3,.... (but not zero)
= ±mπ, where m =1,2,3,.... (but not zero)
Thus the condition of diffraction minimum is
bsinθ = ±mλ (m = 1, 2, 3,...)
The interference term cos2 β gives a set of equidistant dark and a bright fringe as in Young’s double-slit interference experiment. The bright fringe is obtained in the direction
cos2 β =1 ⇒ β = ±nπ ⇒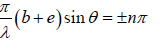
Thus the condition of maximum is
(b + e)sinθ = ±nλ, where n = 0, 1, 2,....
The entire pattern may be considered as consisting of interference fringes due to light from both slits, the intensities of these fringes being governed by the diffraction occurring at the individual slits.

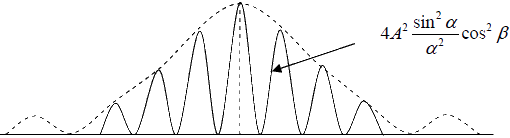
Effect of Slit Width on Diffraction Pattern
- Effect of increasing the slit width
If we increase the slit width b, the envelope of the fringe pattern changes so that it central peak is sharper. The fringe spacing, which depends on slit separation, does not change. Hence less interference maxima now fall within the central diffraction maximum. - Effect of increasing the distance between slits
If b is kept constant and the separation d between them is increased, the fringes become closer together, the envelope of the pattern remains unchanged. Thus more interference maxima fall within the central envelope. - Absent Orders
For certain values of d certain interference maxima become absent from the pattern.
Suppose for some value of θ the following conditions are simultaneously satisfied.
(b + e)sinθ = ±nλ Interference maxima
bsinθ = ±mλ Diffraction minima
Thus according to the first condition, there should be an interference maximum in the directionθ, but according to the second condition, there is no diffracted light in this direction. Therefore, the interference maximum will be absent in this direction.
- If e = b , then n = 2m = 2, 4, 6,.... Since m = 1, 2, 3,....Thus 2nd, 4th and 6th order interference maxima will be absent, i.e. they will coincide with1st, 2nd, 3rd order diffraction minima. Thus the central diffraction maximum will have three interference (zero-order and two first orders) maxima.
- If e = 2b , then n = 3m = 3,6,9,.... Thus the 3rd, 6th, 9th order interference maxima will coincide with 1st, 2nd, 3rd order diffraction minima. Thus the central diffraction maximum will have five interference maxima.
- If e = 3b, then n = 4m = 4,8,12,.... that is 4th, 8th, 12th ……. order interference maxima will coincide with 1st, 2nd and 3rd order diffraction minima. Thus the central diffraction maximum will have seven inference maxima as shown below.
Diffraction Grating
A diffraction grating is an arrangement equivalent to a large number of parallel slits of equal widths and separated from one-another by equal opaque spaces. It is made by ruling a large number of fine, equidistant and parallel lines on an optically plane glass plate with a diamond point. The rulings scatter the light and are effectively opaque while the un-ruled parts transmit light and act as slits.
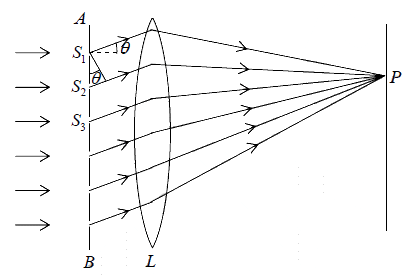
Let AB be the section of a plane transmission grating, the lengths of the slits being perpendicular to the plane of the paper. Let b be the width of each slit and e the width of each opaque space between the slits, then d = b + e is called the grating element.
Let a parallel beam of monochromatic light of wavelength λ be incident normally on the grating. By the theory of Fraunhofer diffraction at a single slit, the wavelets from all points in a slit diffracted in a direction θ are equivalent to a single wave of amplitude 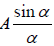 , starting from the middle point of the slit where α =
, starting from the middle point of the slit where α = 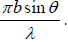
Thus if N be total number of slits in the grating, the diffracted rays from all the slits are equivalent to N parallel rays, one each from the middle points S1, S2, S3 ... of the slits.
Path difference between the rays from the slits S1 and S2 is
S2K = S1S2 sinθ = (b + e) sinθ
The corresponding phase difference = 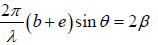
Hence the resultant amplitude in the direction θ is R = 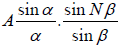
The resultant intensity is I = R2 = 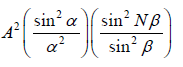
The first term represents the diffraction pattern produced by a single slit whereas the second term represents the Interference pattern produced by N equally spaced slits. For N =1 the above equation reduces to a single slit diffraction pattern and for N = 2 , to the double-slit diffraction pattern.
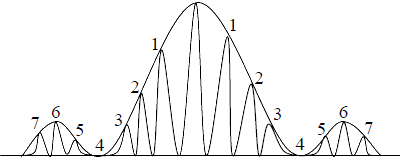
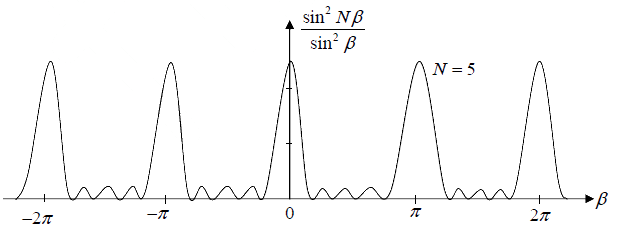
The following figure shows the plot of 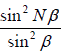 as a function of β for N = 5. As the value of N becomes very large, the above function becomes narrow and very sharply peaked at β = 0, π, 2π ....
as a function of β for N = 5. As the value of N becomes very large, the above function becomes narrow and very sharply peaked at β = 0, π, 2π ....
Between the two peaks, the function vanishes when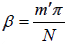 m' 1, 2, 3,..... but m′ ≠ 0, +N, +2N.....
m' 1, 2, 3,..... but m′ ≠ 0, +N, +2N.....
which are referred to as interference minima.
|
54 videos|22 docs|14 tests
|
FAQs on Diffraction of Light - Oscillations, Waves & Optics - Physics
| 1. What is diffraction of light? |  |
| 2. How does the slit width affect the diffraction pattern? |  |
| 3. What is the relationship between the slit width and the intensity of the diffraction pattern? |  |
| 4. How does the wavelength of light affect the diffraction pattern? |  |
| 5. What is the significance of studying diffraction of light in the context of IIT JAM? |  |

|
Explore Courses for Physics exam
|

|
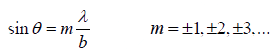
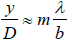
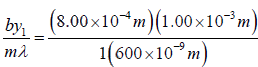 = 1.33m
= 1.33m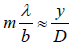 where small-angle approximation has been made.
where small-angle approximation has been made.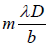
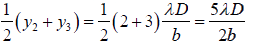
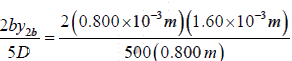 = 6.40 x 10-7m
= 6.40 x 10-7m