Dimensional Analysis | Fluid Mechanics for Civil Engineering - Civil Engineering (CE) PDF Download
Introduction
- Dimensional Analysis is used in research work and for conducting model tests.
- It deals with the dimensions of physical quantities.
- All physical quantities are measured by comparison with length(L), Mass(M), Time(T) (These dimensions are called fundamental dimensions.)
They possess more than one fundamental dimension i.e. Velocity is LT-1
It means the dimensions of each term on both sides of the equation should be equal. Thus, if each term of any equation has the same dimensions on both sides, then it is known as the dimensionally homogenous equation.
Method of Dimensional Analysis
If the number of variables involved in a physical phenomenon is known, then the relationship among variables can be determined by two methods:
- Rayleigh method
- Buckingham -theorem
- Rayleigh Method
It is used to establish the relation for a variable that depends on three or more variables.
Let X be a variable that depends on X1, X2, X3 then, according to the Rayleigh method
X = f (X1, X2, X3)
X = kX1aX2bX3c - Buckingham π- theorem
It defines that “Any problem having n variables and out of which m variables have primary dimensions (such as M, L, T) then equation establishing a relation between all the variables will have (n-m) dimensionless groups”.
Buckingham referred to these groups as π groups and the equation containing these π groups can be written in the form of:
πl = f (π2, π3,……. πn-m)
To solve the equation using this method there are two conditions taken into consideration:
(i) Each of the fundamental dimensions must be present in at least one of the variables.
(ii) A dimensionless group must not be formed from one of the variables within a recurring set.
(iii) A recurring/repeating set is a group of variables that form a dimensionless group.
Method of Selecting Repeating Variables
In any problem, the number of repeating variables is the same as the number of fundamental dimensions. The choice of repeating variables is chosen with the consideration of the following points:
(a) The dependent variable should not be a repeating variable
(b) The selection of repeating variables should be in such a manner that one of the variables should represent the geometric property, the other should be flow property and the third variable should be fluid property.
Variables with geometric property
- Length(L)
- Diameter(d)
- Height etc.
Variables with flow property
- Velocity(v)
- Acceleration etc.
Variables with fluid property
- Dynamic viscosity (μ)
- Density (ρ) etc.
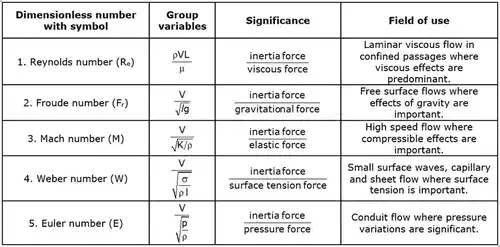
Various Forces in Fluid Mechanics
- Inertia force (Fi): It is defined as the product of mass and acceleration of the flowing fluid and acts in such a direction that it opposes the acceleration.
Fi = ρL2V2 - Surface tension force (Fs): It is defined as the product of surface tension and length of the surface of the flowing fluid.
Fs =σ L - Gravity force (Fg): It is defined as the product of mass and acceleration resulting from the gravity of the flowing fluid.
Fg = ρl3g - Pressure force (FP): It is equal to the product of pressure intensity and cross-sectional area of the flowing fluid.
FP = P × A ⟹ FP = PL2 - Viscous force (Fv): It is defined as the product of shear stress (τ) resulting from viscosity and surface area (As) of the flow
Fv = μLv - Elastic force (Fe): It is defined as the product of elastic stress and area (A) of the flowing fluid.
Fe = KL2
Similitude & Modeling
(i) Geometric similarity: if the ratio of corresponding dimensions of model & Prototype is same.
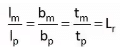
(ii) For kinematic similarity, Geometric Similarity is mandatory.

(iii) For dynamic similarity, geometric and kinematic similarities are mandatory.
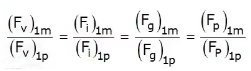
Reynold’s Model Law:
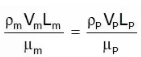
Froude’s Model Law:
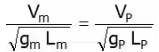
Euler’s model law:
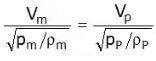
Weber model law:
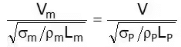
Mach Model Law:
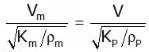
- The models which are geometrically similar to their prototypes are called Undistorted models. In other words, the same scale ratio is taken for the linear dimensions of the model and its prototype.
- If a model is not geometrically similar to its prototype, then it is a distorted model.
- In distorted models, different scale ratios are taken for linear dimensions i.e. different scale ratios are preferred for horizontal and vertical dimensions.
- Example: For the rivers, reservoirs etc., two different scale ratios are taken: one for horizontal dimensions and the other for the vertical dimension.
|
54 videos|94 docs|110 tests
|
|
54 videos|94 docs|110 tests
|

|
Explore Courses for Civil Engineering (CE) exam
|

|