Distance Between Two Points | Mathematics for ACT PDF Download

Distance between two points is the length of the line segment that connects the two given points. Distance between two points in coordinate geometry can be calculated by finding the length of the line segment joining the given coordinates. Let us understand the formula to find the distance between two points in a two-dimensional and three-dimensional plane.

What is the Distance Between Two Points?

The distance between any two points is the length of the line segment joining the points. There is only one line passing through two points. So, the distance between two points can be calculated by finding the length of this line segment connecting the two points. For example, if A and B are two points and if AB =10 cm, it means that the distance between A and B is 10 cm.

The distance between two points is the length of the line segment joining them (but this CANNOT be the length of the curve joining them). Note that the distance between two points is always positive.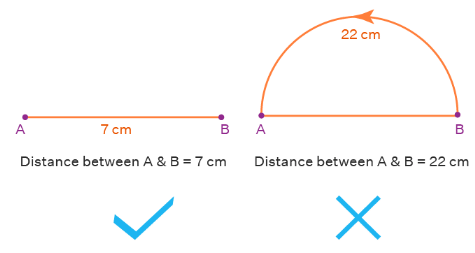

Distance Between Two Points Formula

The distance between two points using the given coordinates can be calculated by applying the distance formula. For any point given in the 2-D plane, we can apply the 2D distance formula or the Euclidean distance formula given as,

Formula for Distance Between Two Points:

The formula for the distance, d d, between two points whose coordinates are (x₁, y₁) and (x₂, y₂) is:
d = √[(x₂ − x₁)² + (y₂ − y₁)²]
This is called the Distance Formula.
To find the distance between two points given in 3-D plane, we can apply the 3D distance formula, given as,
d = √[(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²]

Derivation of Formula for Distance Between Two Points

To derive the formula to calculate the distance between two points in a two-dimensional plane, let us assume that there are two points with the coordinates given as, A(x₁, y₁) B(x₂, y₂)
Next, we will assume that the line segment joining A and B is AB = d. Now, we will plot the given points on the coordinate plane and join them by a line.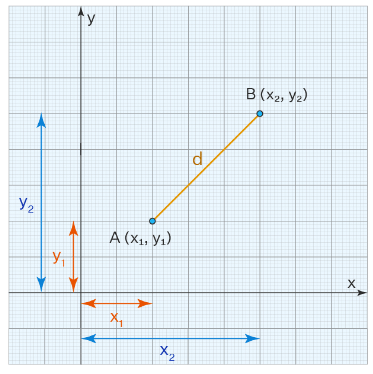

Next, we will construct a right-angled triangle with AB as the hypotenuse.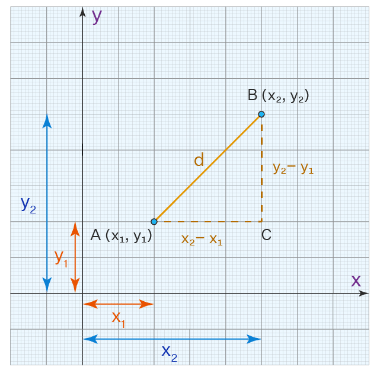

Applying Pythagoras theorem for the △ABC:
AB² = AC² + BC²
d2 = ( x₂ − x₁ )² + ( y₂ − y₁ )² (Values from the figure)
Here, the vertical distance between the given points is |y₂ − y₁|.
The horizontal distance between the given points is |x₂ − x₁|.
d = √[(x₂ − x₁)² + (y₂ − y₁)²] (Taking square root on both sides)
Thus, the distance formula to find the distance between two points is proved.

Note: In case the two points A and B are on the x-axis, i.e. the coordinates of A and B are (x₁, 0) and (x₂, 0) respectively, then the distance between two points AB = |x₂ − x₁|.

Using similar steps and concept, we can also derive the formula to find the distance between two points given in the 3D plane.

How to Find Distance Between Two Points?

The distance between two points using the given coordinates can be calculated with the help of the following given steps:

• Note down the coordinates of the two given points in the coordinate plane as, A(x₁ , y₁) and B(x₂ , y₂).
• We can apply the distance formula to find the distance between the two points, d = √[(x₂ − x₁)² + (y₂ − y₁)²]
• Express the given answer in units.

Note: We can apply the 3D distance formula in case the two points are given in 3D plane, d = √[(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²]

Distance Between Two Points in Complex Plane

The distance between two points in a complex plane or two complex numbers z₁ = a + ib and z₂ = c + id in the complex plane is the distance between points (a, b) and (c, d), given as,
|z₁ − z₂| = √[(a − c)² + (b − d)²]