Theorem | Basic Physics for IIT JAM PDF Download
Divergence Theorem:
The divergence theorem, more commonly known especially in older literature as Gauss's theorem (e.g., Arfken 1985) and also known as the Gauss-Ostrogradsky theorem, is a theorem in vector calculus that can be stated as follows. Let V be a region in space with boundary 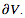 . Then the volume integral of the divergence ∇.F of F over V and the surface integral of F over the boundary
. Then the volume integral of the divergence ∇.F of F over V and the surface integral of F over the boundary 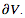 of V are related by
of V are related by
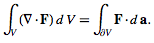
The divergence theorem is a mathematical statement of the physical fact that, in the absence of the creation or destruction of matter, the density within a region of space can change only by having it flow into or away from the region through its boundary.
A special case of the divergence theorem follows by specializing to the plane. Letting S be a region in the plane with boundary 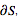 , equation (1) then collapses to
, equation (1) then collapses to
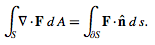
If the vector field F satisfies certain constraints, simplified forms can be used. For example, if F (x,y,z,)=v(x,y,z)c where c is a constant vector ≠0, then
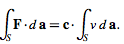
But 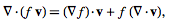
so 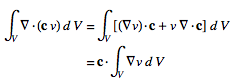
and 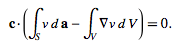
But c≠0 and c.f(v) must vary with v so that c.f(v) cannot always equal zero. Therefore,
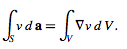
Similarly, if F (x,y,z)=cxP(x,y,z), where c is a constant vector ≠0, then
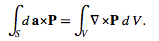
Gauss's theorem:
We know that there is always a static electric field around a positive or negative electrical charge and in that static electric field there is a flow of energy tube or flux. Actually this flux is radiated/emanated from the electric charge. Now amount of this flow of flux depends upon the quantity of charge it is emanating from. To find out this relation, the Gauss’s theorem was introduced. This theorem can be considered as one of the most powerful and most useful theorem in the field of electrical science. We can find out the amount of flux radiated through the surface area surrounding the charge from this theorem.
This theorem states that the total electric flux through any closed surface surrounding a charge, is equal to the net positive charge enclosed by that surface.
Suppose the charges Q1, Q2_ _ _ _Qi, _ _ _ Qn are enclosed by a surface, then the theorem may be expressed mathematically by surface integral as 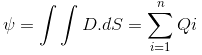
Where, D is the flux density in coulombs/m2 and dS is the outwardly directed vector.
Explanation of Gauss’s Theorem:
For explaining the Gauss’s theorem, it is better to go through an example for proper understanding.
Let Q be the charge at the center of a sphere and the flux emanated from the charge is normal to the surface. Now, this theorem states that the total flux emanated from the charge will be equal to Q coulombs and this can be proved mathematically also. But what about when the charge is not placed at the center but at any point other than the center (as shown in the figure).
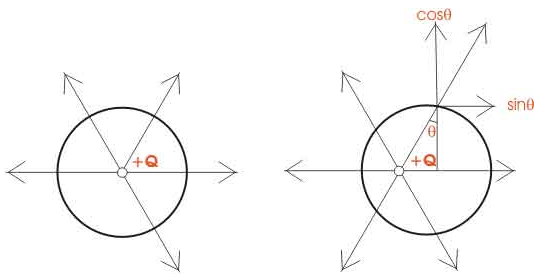
At that time, the flux lines are not normal to the surface surrounding the charge, then this flux is resolved into two components which are perpendicular to each other, the horizontal one is the sinθ component and the vertical one is the cosθ component. Now when the sum of these components is taken for all the charges, then the net result is equal to the total charge of the system which proves Gauss’s theorem.
Proof of Gauss’s Theorem
Let us consider a point charge Q located in a homogeneous isotropic medium of permittivity ε.
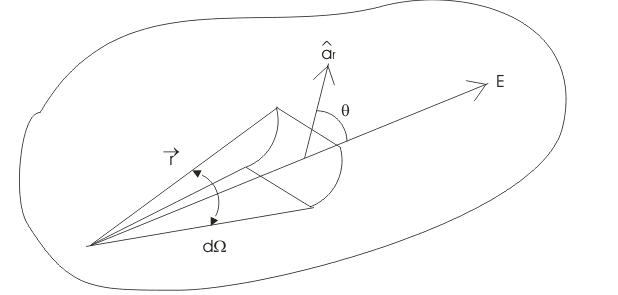
The electric field intensity at any point at a distance r from the charge is
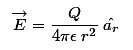
The flux density is given as, 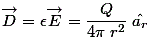
Now from the figure the flux through area dS

Where, θ is the angle between D and the normal to dS.
Now, dScosθ is the projection of dS is normal to the radius vector. By definition of a solid angle
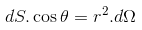
Where, dΩ is the solid angle subtended at Q by the elementary surface are dS. So the total displacement of flux through the entire surface area is
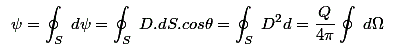
Now, we know that the solid angle subtended by any closed surface is 4π steradians, so the total electric flux through the entire surface is 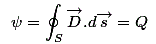
This is the integral form of Gauss’s theorem. And hence this theorem is proved.
Stokes's theorem:
For ω a differential (k-1)-form with compact support on an oriented K-dimensional manifold with boundary M,
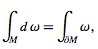 (1)
(1)
where dω is the exterior derivative of the differential form ω. When M is a compact manifold without boundary, then the formula holds with the right hand side zero.
Stokes' theorem connects to the "standard" gradient, curl, and divergence theorems by the following relations. If f is a function on R3,
grad(f)=c-1df, (2)
where c:R3 →R3 (the dual space) is the duality isomorphism between a vector space and its dual, given by the Euclidean inner product on R3. If f is a vector field on a R3,
div (f) = *d* c(f), (3)
where * is the Hodge star operator. If f is a vector field on R3,
curl(f)=c-1*dc(f). (4)
With these three identities in mind, the above Stokes' theorem in the three instances is transformed into the gradient, curl, and divergence theorems respectively as follows. If f is a function on R3 and ϒ is a curve in R3, then
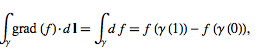 (5)
(5)
which is the gradient theorem. If f:R3→R3 is a vector field and M an embedded compact 3-manifold with boundary in R3, then
 (6)
(6)
which is the divergence theorem. If f is a vector field and M is an oriented, embedded, compact 2-manifold with boundary in R3, then
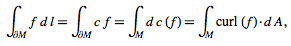 (7)
(7)
which is the curl theorem.
de Rham cohomology is defined using differential k-forms. When N is a submanifold (without boundary), it represents a homology class. Two closed forms represent the same cohomology class if they differ by an exact form, ω1, ω2 =dn. Hence,
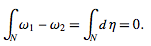 (8)
(8)
Therefore, the evaluation of a cohomology class on a homology class is well-defined. Physicists generally refer to the curl theorem
 (9)
(9)
as Stokes' theorem.
A special case of Stokes' theorem in which F is a vector field and M is an oriented, compact embedded 2-manifold with boundary in R3, and a generalization of Green's theorem from the plane into three-dimensional space. The curl theorem states
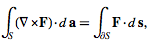 (10)
(10)
where the left side is a surface integral and the right side is a line integral.
There are also alternate forms of the theorem. If
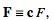 (11)
(11)
then 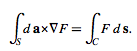 (12)
(12)
and if 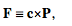 (13)
(13)
then 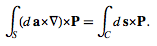 (14)
(14)
|
210 videos|156 docs|94 tests
|
FAQs on Theorem - Basic Physics for IIT JAM
| 1. What is the definition of a theorem in physics? |  |
| 2. How are theorems in physics different from laws? |  |
| 3. Can you give an example of a famous theorem in physics? |  |
| 4. How are theorems used in solving physics problems? |  |
| 5. Are theorems in physics subject to change or revision? |  |

|
Explore Courses for Physics exam
|

|


















