Doc 1: Practice Questions for Quantitative Reasoning | Quantitative Reasoning for UCAT PDF Download
Quantitative Reasoning Practice Questions
The Quantitative Reasoning subtest assesses your ability to use numerical skills to solve problems. It assumes familiarity with numbers to the standard of a good pass at GCSE Questions are less to do with numerical facility and more to do with problem solving.
- You are presented with questions that most often refer to charts and graphs containing data.
- Most questions are shown as sets of four questions each connected to the same data. There are some questions that are standalone and do not share data.
- Each question has five answer options. You are only able to select one response.
Q.1. The table shows the total tax paid, in dollars, on annual taxable income.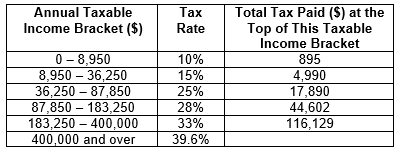
For example, a person with an annual taxable income of $60,000 will pay $4,990 plus 25% of ($60,000 − $36,250).
Q. Bill has an annual taxable income of $28,950.
To the nearest dollar, the income tax he has to pay is:
(a) $2,895
(b) $3,895
(c) $4,342
(d) $4,510
(e) $5,237
Correct Answer is Option (b)
Bill pays $895 on his first $8,950.Remaining taxable income: $28,950 − $8,950 = $20,000
15% tax on $20,000 = $3,000
Total tax: Tax from lowest tax bracket ($895) + tax from next bracket ($3,000) = $3,895
Q.2. The table shows the total tax paid, in dollars, on annual taxable income.
For example, a person with an annual taxable income of $60,000 will pay $4,990 plus 25% of ($60,000 − $36,250).
Q. Omar has a taxable income of $36,250 per year.
What percentage, correct to one decimal place, of his taxable income does Omar pay in tax?
(a) 11.3%
(b) 12.5%
(c) 13.8%
(d) 15.0%
(e) 16.0%
Correct Answer is Option (c)
The second row of the table explains that the total tax paid at the top of this taxable income bracket is $4,990. Omar's taxable income of $36,250 is at the top of this income bracket.$4,990 as a percentage of Omar's taxable income:
$4,990 ÷ $36,250 x 100 = 13.8% correct to one decimal place
Q.3. The table shows the total tax paid, in dollars, on annual taxable income.
For example, a person with an annual taxable income of $60,000 will pay $4,990 plus 25% of ($60,000 − $36,250).
Q. Cory has an annual taxable income equivalent to $2,500 per month. She wants to save enough money each month to pay her tax for the year.
The minimum amount, to the nearest dollar, that Cory has to save each month is:
(a) $250
(b) $263
(c) $338
(d) $341
(e) $375
Correct Answer is Option (c)
Annual taxable income: Monthly taxable income ($2,500) x months in the year (12) = $30,000Amount of tax on annual taxable income:
$895 on the first $8,950Remaining taxable income: $30,000 − 8,950 = $21,050
15% tax on $21,050 = $3,157.50
Total tax: Tax from lowest tax bracket ($895) + tax from next bracket ($3,157.50) = $4,052.50
Total amount to save every month to pay yearly tax: Total tax ($4,052.50) ÷ months in the year (12) = $338 to the nearest dollar
Q.4. The table shows the total tax paid, in dollars, on annual taxable income.
For example, a person with an annual taxable income of $60,000 will pay $4,990 plus 25% of ($60,000 − $36,250).
Q. The values at the bottom end points and at the top end points of each income tax bracket are going to be increased by 10%.
What will be the change in income, to the nearest dollar after tax has been deducted, of a person with a taxable income of $36,250?
(a) $544 decrease
(b) $499 decrease
(c) $45 increase
(d) $351 increase
(e) $543 increase
Correct Answer is Option (c)
In the lowest tax bracket, $8,950 increases by 10% = $9,84510% tax of $9,845 = $984.50
Amount of taxable income remaining: $36,250 − $9,845 = $26,405
15% tax of $26,405 = $3,960.75
Total tax: Tax from the lowest tax bracket ($984.50) + tax from the next tax bracket ($3,960.75) = $4,945.25
The highest amount of tax on the old system for an income of 36,250 = $4,990
Change in income:
(New amount of tax) $36,250 - $4,945.25 = $31,304.74(Old amount of tax) $36,250 - $4,990 = $31,260
Q.5. Here is some information about costs of purchasing land.
Prime farmland is £7,500 per acre.
Building land is £1.1 million per hectare.
The table shows the costs, in thousands of pounds per hectare, of cleaning sites. These are paid in addition to the cost of purchasing the land.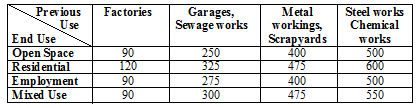
1 hectare = 10,000 m2 = 2.47 acres
Q. How many whole hectares of prime farmland could be bought for the total cost of buying a 1 hectare derelict factory site and cleaning it for residential use?
(a) 39
(b) 65
(c) 162
(d) 362
(e) 401
Correct Answer is Option (b)
(1,100,000 + 120,000) ÷ 7500 = 162.6.., 162.6.. ÷ 2.47 = 65.83
Q.6. Here is some information about costs of purchasing land.
Prime farmland is £7,500 per acre.
Building land is £1.1 million per hectare.
The table shows the costs, in thousands of pounds per hectare, of cleaning sites. These are paid in addition to the cost of purchasing the land.
1 hectare = 10,000 m2 = 2.47 acres
Q. A brownfield site is rectangular, 0.7 km by 1.6 km. It was previously the site of a steelworks. Work out the total cost of buying the land and cleaning it up for residential use.
(a) £79.52 million
(b) £123.2 million
(c) £123.8 million
(d) £179.2 million
(e) £190.4 million
Correct Answer is Option (e)
Area = 700 × 1,600 = 1,120,000 m² = 112 hectares112 × (1.1 million + 0.6 million) = £190.4 million
Q.7. Here is some information about costs of purchasing land.
Prime farmland is £7,500 per acre.
Building land is £1.1 million per hectare.
The table shows the costs, in thousands of pounds per hectare, of cleaning sites. These are paid in addition to the cost of purchasing the land.
1 hectare = 10,000 m2 = 2.47 acres
Q. A plot of building land is square. The length of a diagonal of the plot is 120 m.
Which one of the amounts below is closest in value to the cost of buying the plot?
(a) £396,000
(b) £792,000
(c) £1,528,000
(d) £1,584,000
(e) £3,168,000
Correct Answer is Option (b)
The length of the diagonal of the plot is 120m so we can work out the area by finding out the sides of the square using Pythagoras theorem:120² = side 1² x side 2²
14,400 = 2 x side²
14,400 ÷ 2 = side²
Area of a square = side²
So the area of this square = 7,200m²
The price for building land is in hectares and as 10,000 m² equals one hectare, then this land is 72% of a hectare.
72% of the price of one hectare is £792,000.
Q.8. Here is some information about costs of purchasing land.
Prime farmland is £7,500 per acre.
Building land is £1.1 million per hectare.
The table shows the costs, in thousands of pounds per hectare, of cleaning sites. These are paid in addition to the cost of purchasing the land.
1 hectare = 10,000 m2 = 2.47 acres
Q. Building developers buy an old sewage works site with an area of 4 acres. They intend to clean the site for residential use. They know they can use an area of 1/10th of an acre for a house. Work out the total cost, to the nearest £, of buying and cleaning the land per house.
(a) £44,534
(b) £54,656
(c) £57,677
(d) £142,500
(e) £230,769
Correct Answer is Option (c)
4 ÷ 2.47 = 1.619, 1.619 × (325,000 + 1.100,000) = £2,307,075£2,307,075 ÷ (4 × 10) = 57,676.875
Q.9. The graph shows the velocity of two cars at different times.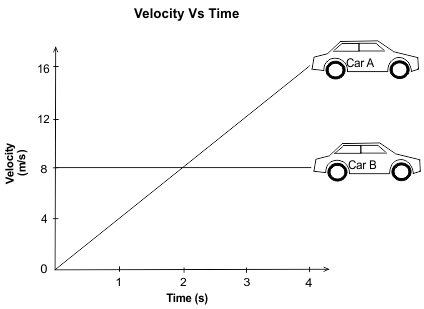
Q. How much greater is the acceleration of Car A than the acceleration of Car B?
[Acceleration (m/s2) = Change in velocity (m/s) ÷ Change in time (s)]
(a) 4 m/s2
(b) 6 m/s2
(c) 8 m/s2
(d) 12 m/s2
(e) 16 m/s2
Correct Answer is Option (a)
Acceleration for Car A = change in velocity/change in time = (16 – 0) / (4 – 0) = 4 m/s²
Acceleration for Car B = change in velocity/change in time = (8 - 8) / (4 - 0) = 0/4 = 0 m/s²
Therefore, Car A is moving with a constant acceleration of 4 m/s², whereas car B is moving with an acceleration of 0 m/s². Difference = 4 m/s²
Q.10. The graph shows Linda’s scores in four projects in her first year at university.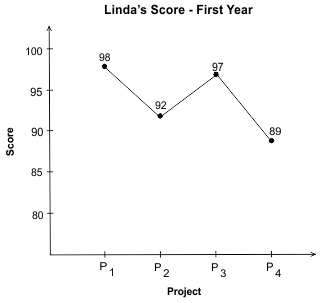 In her 2nd year at university, Linda scored 99 points in P5. What is the difference between her P5 score in the 2nd year and her average project score in the 1st year?
In her 2nd year at university, Linda scored 99 points in P5. What is the difference between her P5 score in the 2nd year and her average project score in the 1st year?
(a) 2
(b) 3
(c) 4
(d) 5
(e) 6
Correct Answer is Option (d)
Linda’s average score in the 1st year = sum of scores in 4 projects/4 = (98 + 92 + 97 + 89)/4 = 376/4 = 94.In P5 of the 2nd year Linda scored 99 points.
Difference in Linda’s score in P5 of the 2nd year and her average score in the 1st year = 99 – 94 = 5 points
Q.11. Mineral water is classified on the basis of the amount of dissolved solid minerals it contains. The chart shows the codes for different levels of total dissolved solids (TDS) and the number of mineral water bottles for each code sold at a store.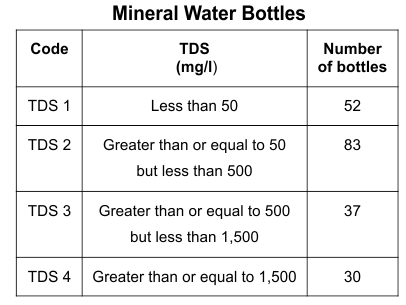
Q. What fraction of the total number of bottles sold at the store with TDS greater than or equal to 50 mg/l, have the code TDS 4?
(a) 7/12
(b) 1/5
(c) 2/25
(d) 3/25
(e) 1/10
Correct Answer is Option (d)
Total number of bottles in the store with TDS greater than or equal to 50 mg/l = 83 + 37 + 30 = 150Number of bottles which have the code TDS 4 = 30
Required fraction = 30/150 = 1/5
Q.12. The table shows the percentage of nickel in two coins.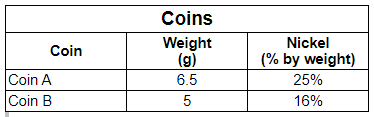
Q. If both the coins are made of only nickel and copper, what is the difference between the weight of copper present in Coin B and the weight of copper in Coin A?
(a) 0.225 g
(b) 0.435 g
(c) 0.560 g
(d) 0.675 g
(e) 0.750 g
Correct Answer is Option (d)
Percentage of copper present in Coin A = 100 – 25 = 75%Amount of copper present in Coin A weighing 6.5 g = 6.5 × 75/100 = 4.875 g
Percentage of copper present in Coin B = 100 – 16 = 84%
Amount of copper present in Coin B weighing 5 g = 5 × 84/100 = 4.2 g
Difference in the amount of copper present in Coin B and Coin A = 4.875 - 4.2 = 0.675 g.
Q.13. A group of people were asked to taste some paper soaked in a weak solution of the chemical PTC. The table gives some information about the results. Q. 3/5 of the women who can taste PTC and 7/12 of the men who can taste PTC do not drink coffee. What percentage, correct to one decimal place, of the adults who can taste PTC do drink coffee.
Q. 3/5 of the women who can taste PTC and 7/12 of the men who can taste PTC do not drink coffee. What percentage, correct to one decimal place, of the adults who can taste PTC do drink coffee.
(a) 33.7%
(b) 41.1%
(c) 43.9%
(d) 58.9%
(e) 66.3%
Correct Answer is Option (b)
35 women and 72 men can taste PTC so:3/5 of women who can taste PTC is 21 (35 ÷ 5 = 7 x 3 = 21)
7/12 of men who can taste PTC is 42 (72 ÷ 12 = 6 x 7 = 42)
In total this is (42 + 21) = 63 adults who can taste PTC and do not drink coffee.
As a percentage this is (63 ÷ 107 = 0.588 x 100) 58.9% to 1 decimal place.
Therefore, the percentage of those that can taste PTC but do drink coffee is 100% - 58.9% = 41.1%
Q.14. A group of people were asked to taste some paper soaked in a weak solution of the chemical PTC. The table gives some information about the results. Q. A population of 100,000 people is equally divided between men, women, boys and girls. Use the data in the table to estimate the number, correct to four significant figures, of people in the population who can taste PTC.
Q. A population of 100,000 people is equally divided between men, women, boys and girls. Use the data in the table to estimate the number, correct to four significant figures, of people in the population who can taste PTC.
(a) 40,020
(b) 41,980
(c) 58,020
(d) 58,610
(e) 59,980
Correct Answer is Option (e)
((35/55) x 25,000)+((72/132)x 25,000)+((18/28) x 25,000) + ((27/47) x 25,000) = 59,980
Q.15. A group of people were asked to taste some paper soaked in a weak solution of the chemical PTC. The table gives some information about the results. Q. If 10% of the men who said they cannot taste PTC could in fact taste PTC at higher concentrations, what would be the ratio of men who can taste PTC to men who cannot taste PTC at higher concentrations?
Q. If 10% of the men who said they cannot taste PTC could in fact taste PTC at higher concentrations, what would be the ratio of men who can taste PTC to men who cannot taste PTC at higher concentrations?
(a) 39:25
(b) 39:27
(c) 39:30
(d) 41:25
(e) 41.30
Correct Answer is Option (b)
78:54 = 39:2760÷10 = 6, 72+6 = 78, 60 - 6 = 54
Q.16. A group of people were asked to taste some paper soaked in a weak solution of the chemical PTC. The table gives some information about the results. Q. Of the adults in the group, what percentage, correct to one decimal place, can taste PTC?
Q. Of the adults in the group, what percentage, correct to one decimal place, can taste PTC?
(a) 40.0%
(b) 40.8%
(c) 57.2%
(d) 58.0%
(e) 59.1%
Correct Answer is Option (c)
35 + 72 + 20 + 60 = 187
35 + 72 = 107 (107÷187) ×100 = 57.2%
Q.17. A courier company's tariff, inclusive of VAT and compensation, is shown in the table.
Q. Two parcels weighing 600 g each were lost during transit. Each parcel was priced at £1,500. The compensation limit was £50 to £1,000 for one parcel and £1,000 to £2,500 for the other. What was the difference between the compensations that the courier company paid for the lost parcels?
(a) £402.83
(b) £503.24
(c) £521.67
(d) £539.58
(e) £618.67
Correct Answer is Option (b)
For the parcel with compensation limit £50 to £1,000, compensation for lost article = Tariff refund + £1,000 or £1,500 (the smaller value is considered) = £19.83 + £1,000 = £1,019.83.For the parcel with compensation limit £1,000 to £2,500, compensation for lost article = Tariff refund + £2,500 or £1,500 (the smaller value is considered) = £23.07 + £1,500 = £1,523.07.
Difference = £1,523.07 - £1,019.83 = £503.24
Q.18. A courier company's tariff, inclusive of VAT and compensation, is shown in the table.
Q. Lucas couriered a cardigan of price £30 and weight 250 g with compensation limit of £0 to £50. If the cardigan is lost during transit, how much compensation should Lucas receive from the company?
(a) £18.14
(b) £30.16
(c) £37.22
(d) £46.09
(e) £50.16
Correct Answer is Option (d)
For a post weighing 250 g and a compensation limit of £0 to £50, the postal tariff = £16.09.The price of the cardigan is £30. The actual price of the cardigan is lower than the maximum limit of compensation which is £50.
Compensation amount = tariff refund + actual price of the cardigan = £16.09 + £30 = £46.09
Q.19. A courier company's tariff, inclusive of VAT and compensation, is shown in the table.
Q. An artefact weighing 900 g and valued at £300 was damaged during transit. It had a compensation limit of £50 to £1,000. If the repairing cost for the artefact is 20% of its value, what is the compensation for the damaged artefact?
(a) £79.83
(b) £81.40
(c) £84.71
(d) £92.40
(e) £96.67
Correct Answer is Option (a)
For a parcel weighing 900 g and a compensation limit of £50 to £1,000, the tariff = £19.83.The cost of the artefact is £300. Amount spent on repairing the damage = 20 × £300/100 = £60.
Compensation amount = tariff refund + repairing cost = £19.83 + £60 = £79.83
Q.20. A courier company's tariff, inclusive of VAT and compensation, is shown in the table.
Q. Davis couriered an article weighing 120 g with a compensation limit of £1,000 to £2,500. If the article was lost during transit and the company paid £1,121.38 as compensation, what was the actual price of the article?
(a) £1,055
(b) £1,070
(c) £1,100
(d) £1,150
(e) £1,175
Correct Answer is Option (c)
For an article weighing 120 g and a compensation limit of £1,000 to £2,500, the postal tariff = £21.38.The price of the article is x. Compensation amount = tariff refund + actual price of the article.
£1,121.38 = £21.38 + x
£1,121.38 - £21.38 = £1100
|
34 videos|17 docs|16 tests
|

|
Explore Courses for UCAT exam
|

|

















