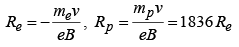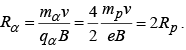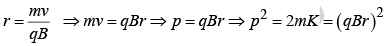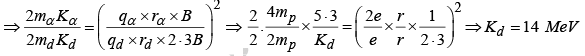Dynamics of Charged Particles in Static and Uniform Electromagnetic Fields | Electricity & Magnetism - Physics PDF Download
The Lorentz Force Law:
The magnetic force on a charge Q, moving with velocity v in a magnetic field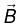 is
is
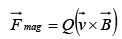
This is known as Lorentz force law.
In the presence of both electric and magnetic fields, the net force on Q would be:
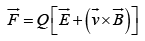
Charged Particle in Static Electric Field
Charged Particle enters in the direction of field (Linear motion)
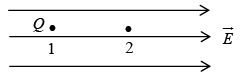
The force on the charge Q in electric field 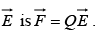
Acceleration of the charge particle in the direction of the electric field is
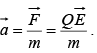
If 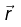 is the position vector at any time t then
is the position vector at any time t then
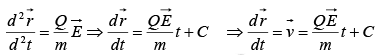
where C is a constant.
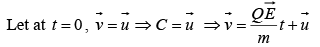
Since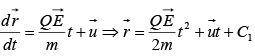
where C1 is a constant
Let at 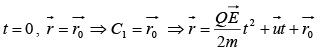
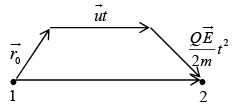
If initially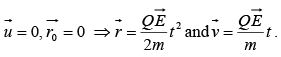
The energy acquired by the charged particle in moving from point 1 to 2 is
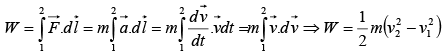
If the potential difference between points 1 to 2 is V then
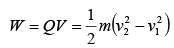
If the particle starts from rest i.e (v1 = 0) and final velocity is v then
Kinetic energy of the particle
Charged Particle enters in the direction perpendicular to field (Parabolic motion)
Let us consider a charge particle enters in an electric field region with velocity vx at t = 0 . The electric field is in the y-direction and the field region has length l. After traversing a distance l it strikes a point P on a screen which is placed at a distance L from the field region.
Since electric field is in the y-direction, charge particle will experience force
In time t, charge particle will traverse a distance 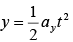 in y-direction and a distance x = vxt in x-direction.
in y-direction and a distance x = vxt in x-direction.
Thus 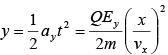 and which represents parabolic path.
and which represents parabolic path.
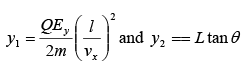
Thus distance of point P from the center of the screen is,
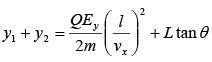
Angle of deviation in the field region
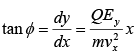
Angle of deviation in the field free region,
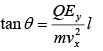
Charged Particle in Static Magnetic Field
he magnetic force on a charge Q, moving with velocity 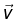 in a magnetic field
in a magnetic field 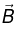 is,
is,
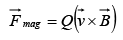
This is known as Lorentz force law.
Charged Particle enters in the direction perpendicular to field (Circular motion)
If a charge particle enters in a magnetic field at angle of 90o, then motion will be circular with the magnetic force providing the centripetal acceleration. As shown in figure, a uniform magnetic field points into the page; if the charge Q moves counter clockwise, with speed v, around a circle of radius R, the magnetic force points inward, and has a fixed magnitude QvB, just right to sustain uniform circular motion:
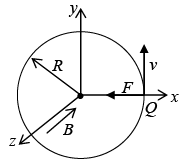
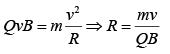
where R is the radius of the circle and m is the mass of the charge particle.
Momentum of the charged particle p = QBR
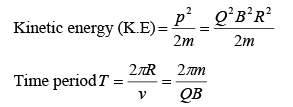
Charged Particle enters in the direction making an angle with the field
(Helical motion)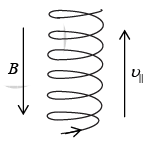
If the charge particle enters in a magnetic field making an angle θ, then motion will be helical.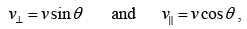 and the radius of helix is
and the radius of helix is 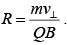
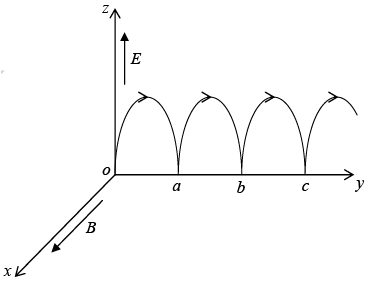
Charged Particle in Uniform Electric and Magnetic Field (Cycloid motion)
If  points in x-direction and
points in x-direction and 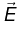 points in z-direction, and a particle at rest is released from origin, then particle will follow cycloid motion. Initially, the particle is at rest, so the magnetic force is zero, and the electric field accelerates the charge in z-direction. As it speeds up, a magnetic force develops which pulls the charge to the right. The faster it goes stronger the magnetic force becomes and it curves the particle back around towards the y-axis. At this point the charge is moving against the electric force, so it begins to slow down-the magnetic force then decreases, and the electrical force takes over, bringing the charge to rest at point a and then process repeats.
points in z-direction, and a particle at rest is released from origin, then particle will follow cycloid motion. Initially, the particle is at rest, so the magnetic force is zero, and the electric field accelerates the charge in z-direction. As it speeds up, a magnetic force develops which pulls the charge to the right. The faster it goes stronger the magnetic force becomes and it curves the particle back around towards the y-axis. At this point the charge is moving against the electric force, so it begins to slow down-the magnetic force then decreases, and the electrical force takes over, bringing the charge to rest at point a and then process repeats.
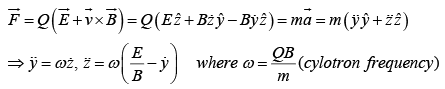
Let us solve the above differential equations,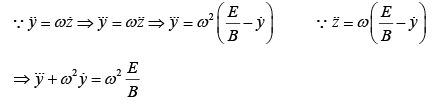
For C.F
For P.I.
Initial Condition: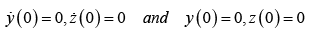
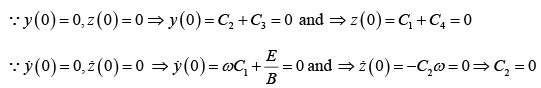
Thus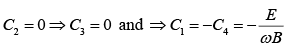
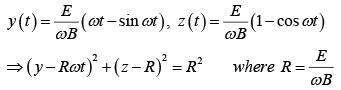
This is the formula for a circle, of radius R, whose center is ( 0, Rω t ,R ) travels in the y-direction at constant speed, 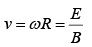
The curve generated in this way is called a cycloid.
Magnetic forces do not work because 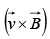 is perpendicular to
is perpendicular to 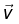
so,
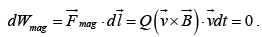
Magnetic forces may alter the direction in which a particle moves, but they can not speed up or slow down it.
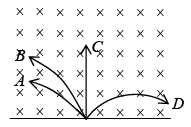
Example 1: A neutron, a proton, an electron and an α – particle enter a region of constant magnetic field with equal velocities. The magnetic field is along the inward normal to the plane of paper. Label the tracks of the particles.
A → Proton, B → α−particle, C → neutron (undeflected), D → electron.
Example 2: A uniform magnetic field with a slit system, as shown in figure, is to be used as a momentum filter for high energy charged particles. With a field B tesla, it is found that the filter transmits α–particles each of energy 5.3 MeV.
The magnetic field is increased to 2.3 B tesla and deuterons are passed into the filter. Find the energy of each deuteron transmitted by the filter.
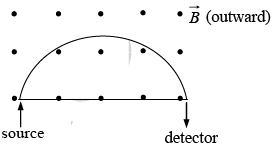
Example 3: A beam of protons with velocity 4 ×105 m / sec enters a uniform magnetic field of 0.3 Tesla at an angle of 600 to the magnetic field. Find the radius of the helical path taken by the proton beam. Also find the pitch of the helix.
v = 4×105m / sec , v⊥ =v sin 60 and v|| =v cos 60
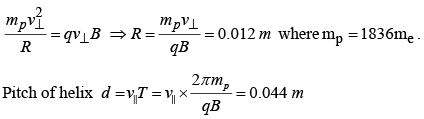
|
82 videos|32 docs|22 tests
|
FAQs on Dynamics of Charged Particles in Static and Uniform Electromagnetic Fields - Electricity & Magnetism - Physics
| 1. What is the Lorentz Force Law? |  |
| 2. What are the applications of the Lorentz Force Law? |  |
| 3. How does the Lorentz Force Law explain the motion of charged particles in electric and magnetic fields? |  |
| 4. Can the Lorentz Force Law be applied to particles with mass but no charge? |  |
| 5. How does the Lorentz Force Law contribute to our understanding of electromagnetic fields? |  |