Early developments: Quantum Theory | Modern Physics for IIT JAM PDF Download
Planck’s Radiation Law
By the end of the 19th century, physicists almost universally accepted the wave theory of light. However, though the ideas of classical physics explain interference and diffraction phenomena relating to the propagation of light, they do not account for the absorption and emission of light. All bodies radiate electromagnetic energy as heat; in fact, a body emits radiation at all wavelengths. The energy radiated at different wavelengths is a maximum at a wavelength that depends on the temperature of the body; the hotter the body, the shorter the wavelength for maximum radiation. Attempts to calculate the energy distribution for the radiation from a black body using classical ideas were unsuccessful. (A black body is a hypothetical ideal body or surface that absorbs and reemits all radiant energy falling on it.) One formula, proposed by Wilhelm Wien of Germany, did not agree with observations at long wavelengths, and another, proposed by Lord Rayleigh (John William Strutt) of England, disagreed with those at short wavelengths.
In 1900 the German theoretical physicist Max Planck made a bold suggestion. He assumed that the radiation energy is emitted, not continuously, but rather in discrete packets called quanta. The energy E of the quantum is related to the frequency ν by E = hν. The quantity h, now known as Planck’s constant, is a universal constant with the approximate value of 6.62607 × 10−34 joule∙second. Planck showed that the calculated energy spectrum then agreed with observation over the entire wavelength range.
Planck’s radiation law, a mathematical relationship formulated in 1900 by German physicist Max Planck to explain the spectral-energy distribution of radiation emitted by a black body (a hypothetical body that completely absorbs all radiant energy falling upon it, reaches some equilibrium temperature, and then reemits that energy as quickly as it absorbs it). Planck assumed that the sources of radiation are atoms in a state of oscillation and that the vibrational energy of each oscillator may have any of a series of discrete values but never any value between. Planck further assumed that when an oscillator changes from a state of energy E1 to a state of lower energy E2, the discrete amount of energy E1 − E2, or quantum of radiation, is equal to the product of the frequency of the radiation, symbolized by the Greek letter ν and a constant h, now called Planck’s constant, that he determined from blackbody radiation data; i.e., E1 − E2 = hν.
Planck’s law for the energy Eλ radiated per unit volume by a cavity of a blackbody in the wavelength interval λ to λ + Δλ (Δλ denotes an increment of wavelength) can be written in terms of Planck’s constant (h), the speed of light (c), the Boltzmann constant (k), and the absolute temperature (T):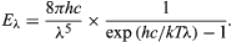
The wavelength of the emitted radiation is inversely proportional to its frequency, or λ = c/ν. The value of Planck’s constant is found to be 6.62606957 × 10−34 joule∙second, with a standard uncertainty of 0.00000029 × 10−34 joule∙second.
For a blackbody at temperatures up to several hundred degrees, the majority of the radiation is in the infrared radiation region of the electromagnetic spectrum. At higher temperatures, the total radiated energy increases, and the intensity peak of the emitted spectrum shifts to shorter wavelengths so that a significant portion is radiated as visible light.
Einstein and the photoelectric effect:
In 1905 Einstein extended Planck’s hypothesis to explain the photoelectric effect, which is the emission of electrons by a metal surface when it is irradiated by light or more-energetic photons. The kinetic energy of the emitted electrons depends on the frequency ν of the radiation, not on its intensity; for a given metal, there is a threshold frequency ν0 below which no electrons are emitted. Furthermore, emission takes place as soon as the light shines on the surface; there is no detectable delay. Einstein showed that these results can be explained by two assumptions: (1) that light is composed of corpuscles or photons, the energy of which is given by Planck’s relationship, and (2) that an atom in the metal can absorb either a whole photon or nothing. Part of the energy of the absorbed photon frees an electron, which requires a fixed energy W, known as the work function of the metal; the rest is converted into the kinetic energy meu2/2 of the emitted electron (me is the mass of the electron and u is its velocity). Thus, the energy relation is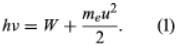
If ν is less than ν0, where hν0 = W, no electrons are emitted. Not all the experimental results mentioned above were known in 1905, but all Einstein’s predictions have been verified since.
Scattering of X-rays:
Soon scientists were faced with the fact that another form of radiation, X-rays, also exhibits both wave and particle properties. Max von Laue of Germany had shown in 1912 that crystals can be used as three-dimensional diffraction gratings for X-rays; his technique constituted the fundamental evidence for the wavelike nature of X-rays. The atoms of a crystal, which are arranged in a regular lattice, scatter the X-rays. For certain directions of scattering, all the crests of the X-rays coincide. (The scattered X-rays are said to be in phase and to give constructive interference.) For these directions, the scattered X-ray beam is very intense. Clearly, this phenomenon demonstrates wave behaviour. In fact, given the interatomic distances in the crystal and the directions of constructive interference, the wavelength of the waves can be calculated.
In 1922 the American physicist Arthur Holly Compton showed that X-rays scatter from electrons as if they are particles. Compton performed a series of experiments on the scattering of monochromatic, high-energy X-rays by graphite. He found that part of the scattered radiation had the same wavelength λ0 as the incident X-rays but that there was an additional component with a longer wavelength λ. To interpret his results, Compton regarded the X-ray photon as a particle that collides and bounces off an electron in the graphite target as though the photon and the electron were a pair of (dissimilar) billiard balls. Application of the laws of conservation of energy and momentum to the collision leads to a specific relation between the amount of energy transferred to the electron and the angle of scattering. For X-rays scattered through an angle θ, the wavelengths λ and λ0 are related by the equation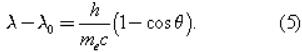
The experimental correctness of Compton’s formula is direct evidence for the corpuscular behaviour of radiation.
De Broglie’s wave hypothesis:
Faced with evidence that electromagnetic radiation has both particle and wave characteristics, Louis-Victor de Broglie of France suggested a great unifying hypothesis in 1924. De Broglie proposed that matter has wave as well as particle properties. He suggested that material particles can behave as waves and that their wavelength λ is related to the linear momentum p of the particle by λ = h/p.
In 1927 Clinton Davisson and Lester Germer of the United States confirmed de Broglie’s hypothesis for electrons. Using a crystal of nickel, they diffracted a beam of monoenergetic electrons and showed that the wavelength of the waves is related to the momentum of the electrons by the de Broglie equation. Since Davisson and Germer’s investigation, similar experiments have been performed with atoms, molecules, neutrons, protons, and many other particles. All behave like waves with the same wavelength-momentum relationship.
|
52 videos|44 docs|15 tests
|
FAQs on Early developments: Quantum Theory - Modern Physics for IIT JAM
| 1. What is quantum theory physics? |  |
| 2. How does quantum theory physics differ from classical physics? |  |
| 3. What are the key principles of quantum theory physics? |  |
| 4. How does quantum theory physics impact our daily lives? |  |
| 5. What are some ongoing challenges in quantum theory physics research? |  |

|
Explore Courses for Physics exam
|

|

















