Eigenvalues and Eigenvectors - Mathematical Methods of Physics | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
Eigenvalues and eigenvectors
Let A = [ aij ] be a given n n square matrix and consider the equation
AX = λX ….(1)
Here X is an unknown vector and λ an unknown scalar and we want to determine both. A value of λ for which (1) has a solution X ≠ 0 is called eigenvalue of the matrix A . The corresponding solutions X ≠ 0 of (1) are called eigenvevtors of A corresponding to that eigenvalue λ .
In matrix notation, (A - λI)X = 0 ….(2)
This homogeneous linear system of equations has a nontrivial solution if and only if the corresponding determinant of the coefficients is zero
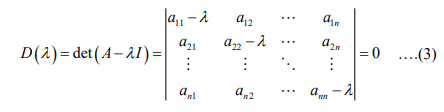
D(λ) is called the characteristic determinant. The equation is called the characteristic equation of the matrix A . By developing D(λ), we obtain a polynomial of nth degree in λ. This is called the characteristic polynomial of A .
Note:
- The eigenvalues of a square matrix A are the roots of the characteristic equation (3) of A . Hence an n x n matrix has at least one eigenvalue and at most n numerically different eigenvalues.
- Once the eigenvalues are known, corresponding eigenvectors are obtained.
- Repeated eigenvalues are said to be degenerate eigenvalues. For degenerate eigenvalues there are different eigenvectors for same eigenvalues.
- Non repeated eigenvalues are non-degenerate eigenvalues. For non-degenerate eigenvalues there are different eigenvectors for different eigenvalues.
- Sum of eigenvalues are equal to trace of matrix
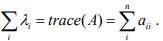 Trace of matrix is sum of diagonal element.
Trace of matrix is sum of diagonal element. - Product of eigenvalues are equal to determinant of matrix
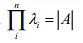
- Eigenvectors correspond to different eigenvalues are always independent.
- Eigenvectors corresponds to same eigenvalue may or may not be independent.
Example 5.1:
To find the eigenvalues and eigenvectors of the matrix
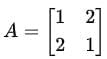
we follow these steps:
Sol:
Step 1: Find the Eigenvalues
We solve the characteristic equation:
det(A−λI)=0
Now compute the determinant:
det(A−λI)=(1−λ)2 −4=λ2 −2λ−3
Solve:
λ2 −2λ−3=0⇒(λ−3)(λ+1)=0
So, the eigenvalues are:
λ1 =3, λ2 =−1
Step 2: Find the Eigenvectors
For λ=3:
Solve 
This gives:
-2x1 + 2x2 = 0 ⇒ x1 = x2
So, an eigenvector is:
For λ=-1:
Solve
This gives:
2x1 + 2x2 = 0 ⇒ x1 = x2
So, an eigenvector is:
- Eigenvalues: 3, -1
- Eigenvectors:
A physics example
There we show the case of two masses, coupled by three springs. We assume that x1 and x2 are the distances of the masses from their equilibrium positions. At that point, we assume the springs are untensioned (neither stretched nor compressed).
The equations of motion take the following simple form: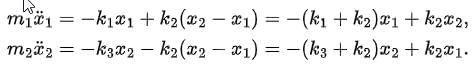
We now take the masses to be equal m1 = m2 = m and all the spring constants to be equal as well (\( k_1 = k_2 = k_3 = k = m \omega^2 \)).
Substituting these values, we find:
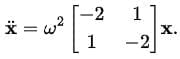
This equation can now be solved by assuming the standard exponential form 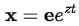 . Substituting this into the equation, we get:
. Substituting this into the equation, we get:
This is an eigenvalue problem. Let 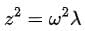 , and we find the eigenvalues λ= -1, -3 . Thus,
, and we find the eigenvalues λ= -1, -3 . Thus, 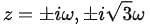 . The eigenvectors corresponding to these eigenvalues are (1, 1) and (1, -1), respectively.
. The eigenvectors corresponding to these eigenvalues are (1, 1) and (1, -1), respectively.
Thus, in all its generality, we find using superposition that:
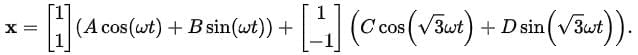
This general motion thus consists of the superposition of two types of motion:
- Motion of the two masses in phase x1 = x2 with frequency ω,
- Motion of the two masses maximally out of phase x1 = -x2 with frequency √3ω.
FAQs on Eigenvalues and Eigenvectors - Mathematical Methods of Physics - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is the significance of eigenvalues and eigenvectors in mathematical methods of physics? |  |
| 2. How are eigenvalues and eigenvectors calculated in mathematical methods of physics? |  |
| 3. Can eigenvalues and eigenvectors have physical interpretations in physics? |  |
| 4. How do eigenvalues and eigenvectors relate to the diagonalization of matrices in mathematical methods of physics? |  |
| 5. What are some applications of eigenvalues and eigenvectors in mathematical methods of physics? |  |

















