Einstein & Debye Theory of Specific Heat | Solid State Physics, Devices & Electronics PDF Download
Einstein and Debye Theory of Specific Heat
Classical Theory
A crystal consists of atoms which are arranged in a periodic manner and are bound togather by strong binding forces.
“In the classical theory it is consumed that each atom of a crystal acts as a three- dimensional harmonic oscillator and all the atoms vibrate independent of one other.” Further a system of N vibrating atoms or N independent three dimensional harmonic oscillators is equivalent to a system of 3N identical and independent one-dimensional Harmonic oscillators.
Assuming that the distribution of oscillators in energy obeys the Maxwell-Boltzmann distribution law the average energy of each harmonic oscillator is given by
According to Equipartition Theory (K.E) = 1/2 kBT
According to Hooks Law (K.E) = (P.E) = 1/2(kBT)
But E =K .E+ P.E
⇒ (E) = 1/2(kBT) + 1/2(kBT) = kBT
Thus the total vibration energy of the crystal containing N identical atoms or 3N onedimensional Harmonic oscillator become
E = 3 N < E >
E = 3NkBT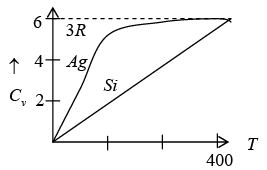
Using the definition of specific heat of CV = (∂E/∂T)V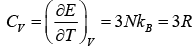
The above result so that the molar specific heat of all the solids is constant and is independent of temperature and frequency this is called Dulog and Petit’s law
Einstein Theory of Specific Heat
Einstein, in 1911, attempted to resolve the discrepancies of the classical theory of specific heat by applying the Planck’s quantum theory. Einstein retained all the assumptions of the classical theory as such except replacing the classical harmonic oscillator by quantum
Harmonic oscillator i.e.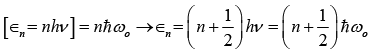
The salient features of the Einstein’s theory are listed as:
- A crystal consist of atoms which may be regarded as identical and independent harmonic oscillator
- A solid consisting of N atoms is equivalent to 3 N one-dimensional harmonic oscillator
- All the oscillators vibrate with the same natural frequency due to the identical environment of each.
- The oscillators are quantum oscillators and have discrete energy
- Any number of oscillators may be present in the same quantum state.
- The atomic oscillators form an assembly of system which are distinguishable or identifiable due to their location at separate and distinct lattice state and hence obey the Maxwell-Boltzmann distribution of energy.
To calculate the average energy of an oscillator, we replace integration by summation in expression for the m-B distribution of energy and obtain.
The expression for the internal energy of the crystal become 
Then,  (let Einstein temperature
(let Einstein temperature 
Case-I:
High temperature behavior 
CV = 3NkB= 3R 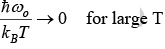
which is the Dulong and Petits law as obtain from classical theory.
Case-II:
Low temperature behavior 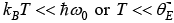

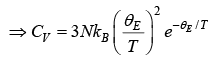
Thus, for T << θE the heat capacity is proportional to e−θE/ T which is the dominating factor. But e rimentally it is found to vary as T3 for most of the solid. 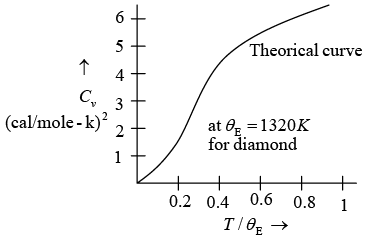
Thus Einstein theory failed to explain actual variation of specific heat.
Debye Theory of Specific Heat
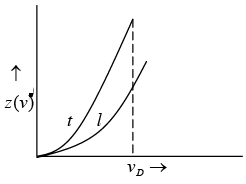
In this model, the vibrational motion of the crystal as a whole was considered to be equivalent to the vibrational motion of system of complete harmonic oscillator which can propagate a range of frequency rather than a single frequency. Debye proposed that crystal can propagate elastic waves of wave lengths ranging from low frequency of (sound wave) to high frequencies corresponding to infrared absorption. This means that a crystal can be a number of modes of vibration. The number of vibration modes per unit frequency range is called density of modes z (v ) .
Thus, the number of possible modes of vibration is 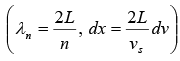
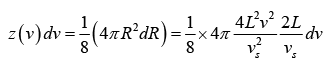
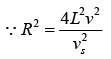
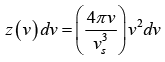
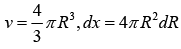
In general, the elastic waves propagating in solid are of two types, transverse waves and longitudinal wave
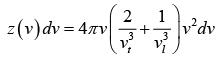
For the total number of vibrational modes with frequencies ranging from zero to vD . We can write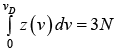
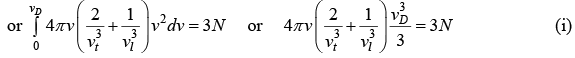
We can associate a Harmonic oscillator of the same frequency with each vibrational mode. Thus, the vibrational energy of the crystal is given by 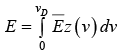
(ii) where 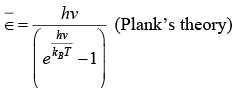
Using equation (i) and (ii) 
Putting 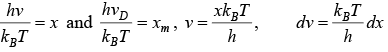
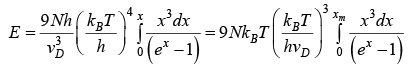
Let Debye temperature is 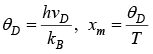
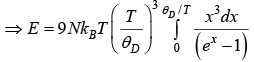
For more general 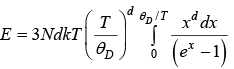
d = 1for 1D, d = 2for 2D, d = 3for 3D
We will discuss for 3 dimension
Case-I: High temperature x >> T >> θD ex − 1 ≈ x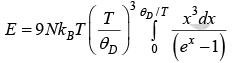 ⇒ E = 3NkBT
⇒ E = 3NkBT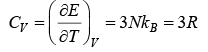 ⇒ CV= 3R
⇒ CV= 3R
Thus, at high temperatures, the Debye’s theory also obeys the Dulong and Petit law as obeyed by classical theory and the Einstein theory.
Case-II: Low temperature
For T << θD ,xm = θD/T → ∞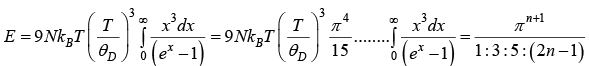
 ⇒ CV ∝ T3
⇒ CV ∝ T3
Thus, at very low temperature, the specific heat is proportional to T3. This is called the debye T3 law.
Note: The heat capacity dependency on temperature in 3D, 2D & 1D as follows 
|
91 videos|21 docs|25 tests
|
FAQs on Einstein & Debye Theory of Specific Heat - Solid State Physics, Devices & Electronics
| 1. What is the Einstein theory of specific heat? |  |
| 2. How does the Debye theory of specific heat differ from the Einstein theory? |  |
| 3. What are the limitations of the Einstein and Debye theories of specific heat? |  |
| 4. How do the Einstein and Debye theories contribute to our understanding of specific heat in solids? |  |
| 5. What are some practical applications of the Einstein and Debye theories of specific heat? |  |
















