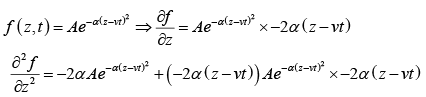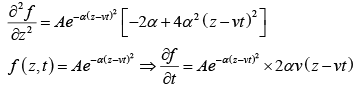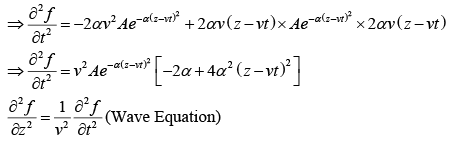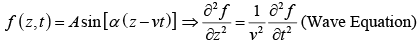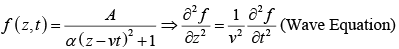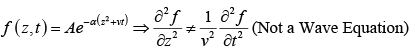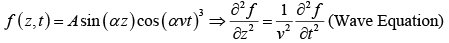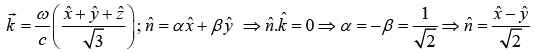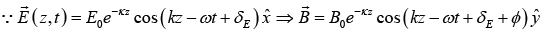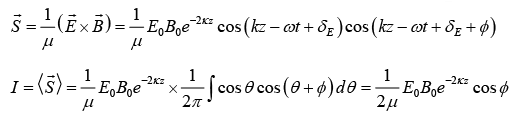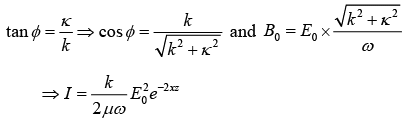Electromagnetic Waves | Electricity & Magnetism - Physics PDF Download
Poynting Theorem (“Work Energy Theorem of Electrodynamics”)
The work necessary to assemble a static charge distribution is 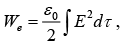 where E is the resulting electric field.
where E is the resulting electric field.
The work required to get currents going (against the back emf) is 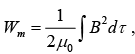 where B is the resulting magnetic field.
where B is the resulting magnetic field.
This suggests that the total energy in the electromagnetic field is
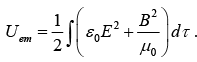
Suppose we have some charge and current configuration which at time t, produces fields
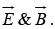 In next instant dt the charges moves around a bit. The work is done by electromagnetic forces acting on these charges in the interval dt .
In next instant dt the charges moves around a bit. The work is done by electromagnetic forces acting on these charges in the interval dt .
According to Lorentz Force Law, the work done on a charge ‘q’ is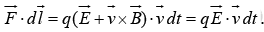
Now  so the rate at which work is done on all the charges in a
so the rate at which work is done on all the charges in a
volume V is 
 is the work done per unit time, per unit volume- which is the power delivered per unit volume. Use Ampere’s–Maxwell law to eliminate
is the work done per unit time, per unit volume- which is the power delivered per unit volume. Use Ampere’s–Maxwell law to eliminate 
Since
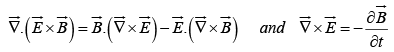
It follows that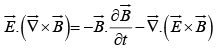
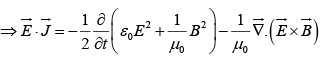
Thus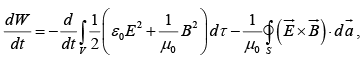
where S is the surface bounding V.
This is Poynting's theorem; it is the “work energy theorem” of electrodynamics. The first integral on the right is the total energy stored in the fields, Uem .
The second term evidently, represents the rate at which energy is carries out of V, across its boundary surface, by the electromagnetic fields.
Poynting's theorem says, that, “the work done on the charges by the electromagnetic force is equal to the decrease in energy stored in the field, less the energy that flowed out through the surface”.
The energy per unit time, per unit area, transported by the fields is called the Poynting vector
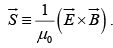
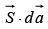 is the energy per unit time crossing the infinitesimal surface
is the energy per unit time crossing the infinitesimal surface 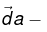 the energy or energy flux density.
the energy or energy flux density.
Waves in One Dimension (Sinusoidal waves)
The Wave Equation
A wave propagating with speed v in z-direction can be expressed as:
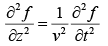
It admits as solutions all functions of the form
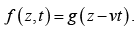
But functions of the form g (z − vt) are not the only solutions. The wave equation involves the square of v, so we can generate another class of solutions by simply changing the sign of the velocity: f(z,t) = h(z+ vt ) .
This, of course, represents a wave propagating in the negative z-direction. The most general solution to the wave equation is the sum of a wave to the right and a wave to the left: f(z,t) = g(z−vt)+ h(z +vt) .
(Notice that the wave equation is linear: the sum of any two solutions is itself a solution.) Every solution to the wave equation can be expressed in this form.
Example 1: Check which of the following functions satisfy the wave equation (where symbols have their usual meaning and A,α are constants of suitable dimensions)
(a) 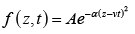
(b) 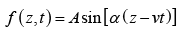
(c) 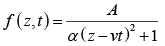
(d) 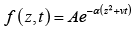
(e) 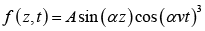
(a)
(b)
(c)
(d)
(e)
Terminology
Let us consider a function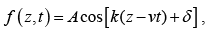 where A is the amplitude of the wave (it is positive, and represents the maximum displacement from equilibrium). The argument of the cosine is called the phase, and δ is the phase constant (normally, we use a value in the range 0 ≤ δ<2π ).
where A is the amplitude of the wave (it is positive, and represents the maximum displacement from equilibrium). The argument of the cosine is called the phase, and δ is the phase constant (normally, we use a value in the range 0 ≤ δ<2π ).
Figure given below shows this function at time t = 0 . Notice that at 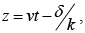 the phase is zero; let's call this the “central maximum.” If δ = 0 , central maximum passes the origin at time t = 0 ; more generally δ/k is the distance by which the central maximum (and therefore the entire wave) is “delayed.”
the phase is zero; let's call this the “central maximum.” If δ = 0 , central maximum passes the origin at time t = 0 ; more generally δ/k is the distance by which the central maximum (and therefore the entire wave) is “delayed.”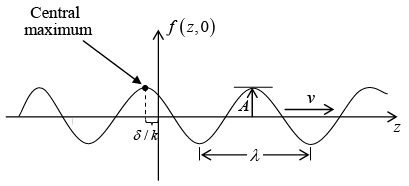
Finally k is the wave number; it is related to the wavelength λ as λ = 2π/k,
for when z advances by 2π/k, the cosine executes one complete cycle.
As time passes, the entire wave train proceeds to the right, at speed v . Time period of one complete cycle is T = 2π/kv.
The frequency ν (number of oscillations per unit time) is 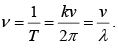
The angular frequency ω = 2πν= kv
In terms of angular frequency ω , the sinusoidal wave can be represented as f(z, t) = A cos ( kz−ω t + δ).
A sinusoidal oscillation of wave number k and angular frequencyω traveling to the left would be written f(z, t) = A cos( kz+ ω t −δ ).
Comparing this with the wave traveling to the right reveals that, in effect, we could simply switch the sign of k to produce a wave with the same amplitude, phase constant, frequency, and wavelength, traveling in the opposite direction.
Complex notation
In view of Euler's formula 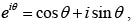
the sinusoidal wave f(z, t) = Acos (kz−ω t + δ) can be written as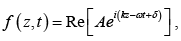
where Re (η) denotes the real part of the complex number η . This invites us to introduce the complex wave function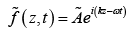
with the complex amplitude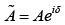 absorbing the phase constant. The actual wave function is the real part of
absorbing the phase constant. The actual wave function is the real part of 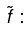
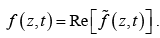
The advantage of the complex notation is that exponentials are much easier to manipulate than sines and cosines.
Polarization
In longitudinal wave, the displacement from the equilibrium is along the direction of propagation. Sound waves, which are nothing but compression waves in air, are longitudinal.
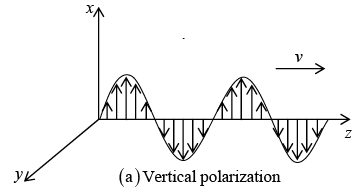
Electromagnetic waves are transverse in nature. In a transverse wave displacement is perpendicular to the direction of propagation.
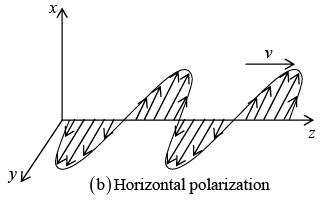
There are two dimensions perpendicular to any given line of propagation. Accordingly, transverse waves occur in two independent state of polarization:
“Vertical” polarization 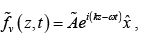
“Horizontal” polarization 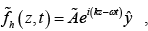
or along any other direction in the xy plane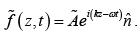
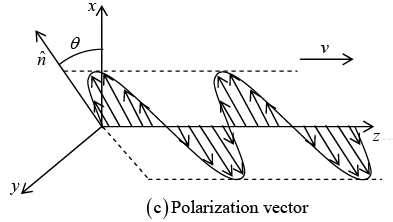
The polarization vector 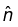 defines the plane of vibration. Because the waves are transverse,
defines the plane of vibration. Because the waves are transverse, 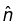 is perpendicular to the direction of propagation:
is perpendicular to the direction of propagation: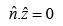
In terms of polarization angleθ ,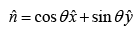
Thus wave in figure(c) can be considered a superposition of two waves-one horizontally polarized, the other vertically: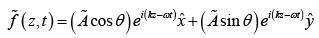
Electromagnetic Waves in Vacuum
The Wave Equation for 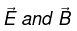
Maxwell’s equations in free space 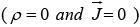 can be written as,
can be written as,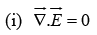
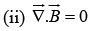
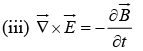
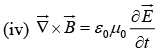
Taking curl of equation (iii) and using equation (i) & (ii) we get,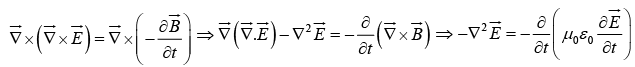
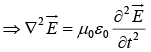
Similarly,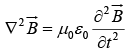
Thus 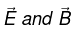 satisfy the wave equation
satisfy the wave equation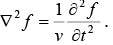
So, EM waves travels with a speed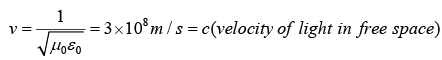
where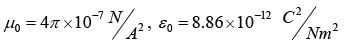
Monochromatic Plane Waves
Suppose waves are traveling in the z-direction and have no x or y dependence; these are called plane waves because the fields are uniform over every plane perpendicular to the direction of propagation.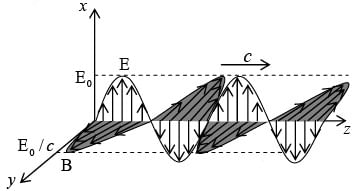
The plane waves can be represented as:
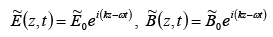
where 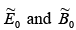 are the (complex) amplitudes (the physical fields, of course are the real part of
are the (complex) amplitudes (the physical fields, of course are the real part of 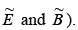
Since 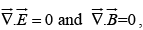 it follows that
it follows that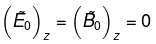
That is, electromagnetic waves are transverse: the electric and magnetic fields are perpendicular to the direction of propagation.
Also,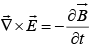
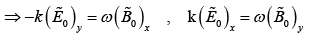
In compact form
Evidently 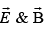 are in phase and mutually perpendicular; their (real) amplitudes are
are in phase and mutually perpendicular; their (real) amplitudes are
related by,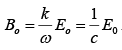
There is nothing special about the z direction; we can generalize the monochromatic plane waves traveling in an arbitrary direction. The propagation vector or wave vector 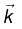 points in the direction of propagation, whose magnitude is the wave number k. The scalar product
points in the direction of propagation, whose magnitude is the wave number k. The scalar product 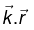 is the appropriate generalization of kz, so
is the appropriate generalization of kz, so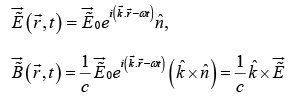
where 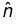 is polarization vector.
is polarization vector.
Also,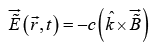
Because 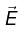 is transverse, (
is transverse, (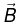 is also transverse):
is also transverse): 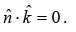
The actual (real) electric and magnetic fields in a monochromatic plane wave with propagation vector 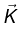 and polarization
and polarization 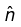 are
are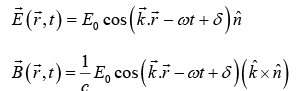
Example 2: Write down the electric and magnetic fields for a plane monochromatic wave of amplitude E0 , frequency ω and phase angle zero that is
(a) Traveling in the y-direction and polarized in the x-direction.
(b) Traveling in the direction from the origin to the point (1,1,1) with polarization parallel to xy plane.
(a)
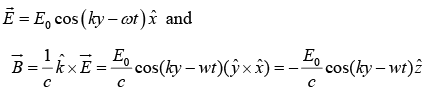
(b)
Energy and Momentum in Electromagnetic Wave
The energy per unit volume stored in electromagnetic field is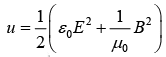
In case of monochromatic plane wave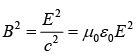
So the electric and magnetic contributions are equal i.e.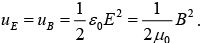
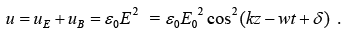
As the wave travels, it carries this energy along with it. The energy flux density (energy per unit area, per unit time) transported by the fields is given by the Pointing vector
For monochromatic plane wave propagating in the z-direction,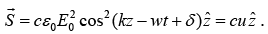
The energy per unit time, per unit area, transported by the wave is therefore uc . Electromagnetic fields not only carry energy, they also carry momentum. The momentum density stored in the field is 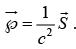
For monochromatic plane wave,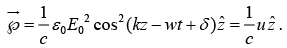
Average energy density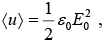
Average of Poynting vector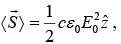
Average momentum density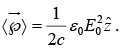
The average power per unit area transported by an electromagnetic wave is called the intensity 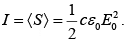
Note:
(a) When light falls on perfect absorber it delivers its momentum to the surface. In a time Δt the momentum transfer is 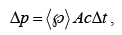
 so the radiation pressure (average force per unit area) is
so the radiation pressure (average force per unit area) is 
(b) When light falls on perfect reflector, the radiation pressure P = 2I/c because the momentum changes direction, instead of being absorbed.
Example 3: The electric and magnetic fields of an electromagnetic waves in the free space are 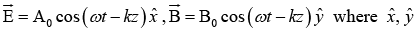 being unit vectors in x and y directions respectively. Then find the intensity of electromagnetic wave.
being unit vectors in x and y directions respectively. Then find the intensity of electromagnetic wave.
Electromagnetic Waves in Matter
Inside matter, but in regions where there is no free charge or free current 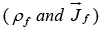 Maxwell’s Equation becomes,
Maxwell’s Equation becomes,
(i)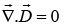
(ii)
(iii)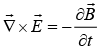
(iv)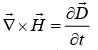
If the medium is linear and homogeneous,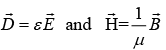
Now the wave equation inside matter is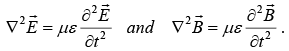
Thus EM waves propagate through a linear homogenous medium at a speed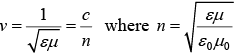
Thus 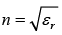 is the index of refraction (since μr = 1 for non-magnetic material).
is the index of refraction (since μr = 1 for non-magnetic material).
The energy density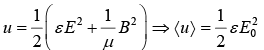
The Poynting vector
Intensity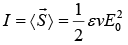
Thus in a medium c →v , ε → ε0 and μ0 → μ
Electromagnetic Waves in Conductors
Any initial free charge density ρf(0) given to conductor dissipate in a characteristic time τ ≡ ε /σ where σ is conductivity and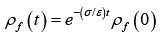
This reflects the familiar fact that if we put some free charge on conductor, it will flow out to the edges.
Free current density in a conductor is 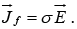
Thus Maxwell’s equations inside conductor are
(i)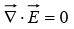
(ii)
(iii)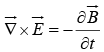
(iv)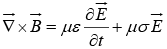
We get modified wave equation for 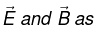
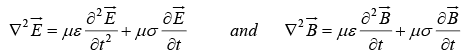
The admissible plane wave solution is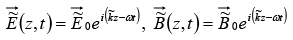 where “wave number”
where “wave number” 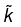 is complex If we put the solution in wave equation, we get
is complex If we put the solution in wave equation, we get 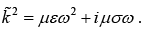
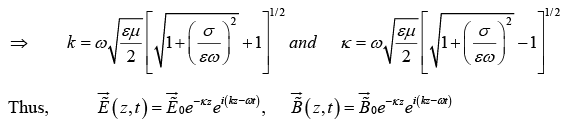
The distance it takes to reduce the amplitude by a factor of 1/e is called the skin depth (d)
d = 1/k;
it is a measure of how far the wave penetrates into the conductor.
The real part of 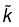 determines the wavelength, the propagation speed, and the index of refraction:
determines the wavelength, the propagation speed, and the index of refraction: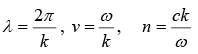
Like any complex number, 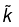 can be expressed in terms of its modulus and phase:
can be expressed in terms of its modulus and phase: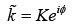
where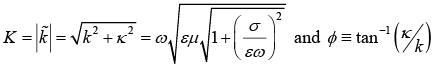
The complex amplitudes 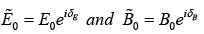 are related by
are related by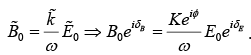
Evidently the electric and magnetic fields are no longer in phase; in fact δB −δE=φ , the magnetic field lags behind the electric fields.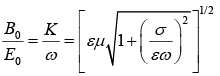
Thus,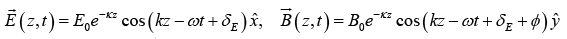
Note:
(a) In a poor conductor (σ << ωε)
(b) In a very good conductor (σ >> ωε)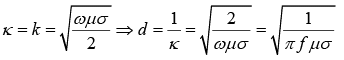
(c) When an electromagnetic wave strikes a perfect conductor (σ →∞ ) then all waves are reflected back i.e. 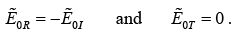
Example 4: An electromagnetic wave of frequency 10 GHz is propagating through a conductor having conductivity 6 ×107 (Ωm)−1 and σ >> ωε . Then find the skin depth of the conductor.
Example 5: An electromagnetic plane wave is propagating inside a conductor with electric field 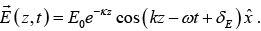 Then calculate the intensity of the wave inside the conductor.
Then calculate the intensity of the wave inside the conductor.
|
82 videos|32 docs|22 tests
|
FAQs on Electromagnetic Waves - Electricity & Magnetism - Physics
| 1. What are electromagnetic waves? |  |
| 2. How are electromagnetic waves produced? |  |
| 3. What is the speed of electromagnetic waves? |  |
| 4. How do electromagnetic waves interact with matter? |  |
| 5. What are some practical applications of electromagnetic waves? |  |