Electrostatic Boundary Condition & Laplace Equation | Electricity & Magnetism - Physics PDF Download
Electrostatics Boundary Conditions
The boundary between two mediums is a thin sheet of surface charge σ . Consider a thin Gaussian pillbox, extending equally above and below the sheet as shown in the figure below:
The Gauss's law states that,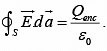
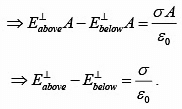
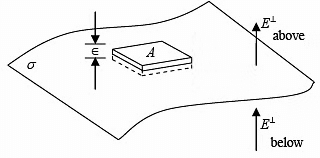
The normal component of 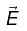 is discontinuous by an amount σ/ε0, at any boundary. If there is no surface charge, E⊥.
is discontinuous by an amount σ/ε0, at any boundary. If there is no surface charge, E⊥.
The tangential component of 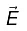 is always continuous.
is always continuous.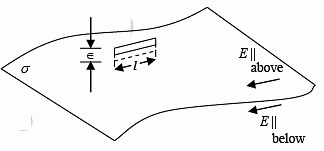
Apply 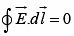 to the thin rectangular loop,
to the thin rectangular loop,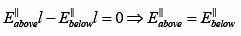 where
where  stands for the components of
stands for the components of 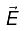 parallel to the surface.The boundary conditions on
parallel to the surface.The boundary conditions on 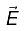 can be combined into the single formula:
can be combined into the single formula: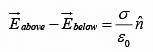 where
where 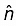 is the unit vector perpendicular to the surface, pointing upward.The potential is continuous across any boundary since
is the unit vector perpendicular to the surface, pointing upward.The potential is continuous across any boundary since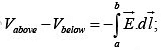 the path shrinks to zero.
the path shrinks to zero.
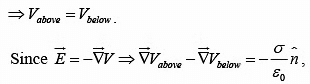
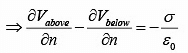
where 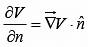 denotes the normal derivative of V (that is the rate of change in the direction perpendicular to the surface).
denotes the normal derivative of V (that is the rate of change in the direction perpendicular to the surface).
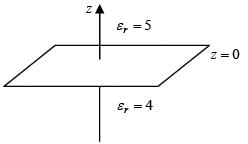
Example 1: Assume that the z = 0 plane is the interface between two linear and homogenous dielectrics (see figure). The relative permittivities are εr = 5 for z > 0 and εr = 4 for z < 0. The electric field in the region z > 0 is 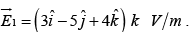
If there are no free charges on the interface, then find an electric field in the region z < 0.
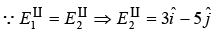
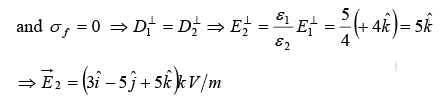
Solution of Laplace’s equation for simple cases
Since, 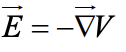 and
and 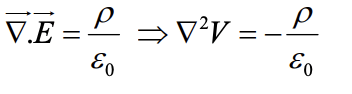
This is known as Poisson's equation.
In regions where there is no charge, so that ρ=0 , Poisson's equation reduces to Laplace's equation,
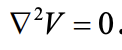
Example 2: Consider two concentric spherical conducting shells centred at the origin. The outer radius of the inner shell is ra and the inner radius of the outer shell is rb . The charge density ρ = 0 in the region ra < r < rb. If V = 0 at r = ra and V = V0 at r = rb, then find V in the region ra < r < rb.
Since voltage is varying only with r, the Laplace’s equation takes the form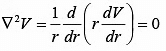 Integrate twice to get the solution V (r ) = A ln ( r ) + Band the boundary conditions are (i) V = 0 at r = ra
Integrate twice to get the solution V (r ) = A ln ( r ) + Band the boundary conditions are (i) V = 0 at r = ra
(ii) V = V0 at r = rb
Substituting these boundary conditions, we get
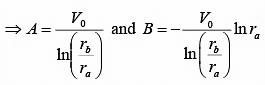 Thus,
Thus,
Example 3: Potential in a region of space is given by, 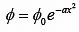 where φ0 and a is constant. Then find the charge density in this region.
where φ0 and a is constant. Then find the charge density in this region.
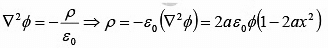
Example 4: If the electrostatic potential was given by φ =φ0 ( x2+ y2 +z2), where φ0 is constant, then find the charge density giving rise to the above potential.
∇2φ = -ρ/ε₀,
where ∇2 is the Laplacian operator and ε₀ is the vacuum permittivity.
Given φ = φ0 (x2 + y2 + z2), we have:
∇2φ = ∂²φ/∂x² + ∂²φ/∂y² + ∂²φ/∂z² = 2φ0 + 2φ0 + 2φ0 = 6φ0.
Now, equating this to -ρ/ε₀, we get:
-ρ/ε₀ = 6φ0
Therefore, the charge density ρ is given by:
ρ = -6ε₀φ0
So, the charge density giving rise to the given potential is -6ε₀φ0
|
82 videos|32 docs|22 tests
|




















