Eleven Check Method | Improve Your Calculations: Vedic Maths (English) - Class 6 PDF Download

Introduction

This method works because adding the digit in a number gives the remainder of the number after division by 9. A similar method works by using remainders of numbers after division by 11 rather than 9.

Alternate digit sum or Eleven-check Method

Suppose we want another check for 2434 × 23 = 55982 it can be done in the following steps:
Step1: Alternately add and subtract (starting from right moving towards left) the digits of each numbers as described below: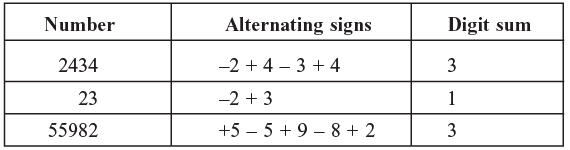

Step 2: Now multiply the Digit Sum to get the product 3 × 1 = 3 Since the Digit Sum of the product and the two numbers is the same, the answer is correct as per 11 check method.
Two digit and Negative number in the digit sum checking the sum of addition
4364 + 1616
Left to right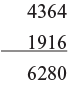

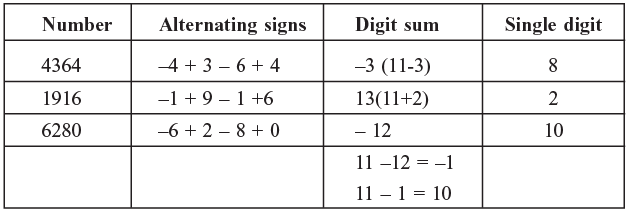
Step 2: Apply the following rules to get a single positive digit for the number 

• Subtract the negative numbers below 11 from 11 to get its positive counterpart so – 3 = 11 –3 = 8 And –12 = –12 +11 = –1 = 11 – 1 = 10
• For the two digit number above 11, divide the number by 11 and get the remainder as the positive digit sum so 13 ÷ 13 gives remainder 2. Alternately, adding and subtracting digit of 13 starting from right can obtain this same result.

Step 3: now add the Digit sums to get the sum 8 + 2 = 10, the answer is correct as per 11 check method.

Two digits in the digit sum 

Check subtraction problem
2819174 – 839472

Step 1: Alternatively add and subtract (starting from right and moving towards left) the digit of each number as described below:
Step 2: Apply the following rules to get a single positive digit for the number 

• The negative numbers below –11 are to be first divided by 11 to get the remainder. Then subtract the remainder from 11 to get its positive counterpart. So –16/11 Remainder is –5 and –5 = 11 – 5 = 6 similarly –15/11 Remainder –4 = 11 –4 = 7. 
• The negative number –1 = 11 – 1 = 10

Step 3: Now subtract the Digit sums to get the answer 6 – 7 = –1 = 10, the answer is correct as per 11- checked method.