Emission & Conductivity | Basic Physics for IIT JAM PDF Download
Emission:
Thermionic Emission:
A metal contains mobile electrons in a partially filled band of energy levels—i.e., the conduction band. These electrons, though mobile within the metal, are rather tightly bound to it. The energy that is required to release a mobile electron from the metal varies from about 1.5 to 6 electron volts, depending on the metal. In thermionic emission, some of the electrons acquire enough energy from thermal collisions to escape from the metal. The number of electrons emitted and therefore the thermionic emission current depend critically on temperature.
In a metal the conduction-band levels are filled up to the Fermi level, which lies at an energy −W relative to a free electron outside the metal. The work function of the metal, which is the energy required to remove an electron from the metal, is therefore equal to W. At a temperature of 1,000 K only a small fraction of the mobile electrons have sufficient energy to escape. The electrons that can escape are moving so fast in the metal and have such high kinetic energies that they are unaffected by the periodic potential caused by atoms of the metallic lattice. They behave like electrons trapped in a region of constant potential. Because of this, when the rate at which electrons escape from the metal is calculated, the detailed structure of the metal has little influence on the final result. A formula known as Richardson’s law (first proposed by the English physicist Owen W. Richardson) is roughly valid for all metals. It is usually expressed in terms of the emission current density (J) as
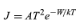
in amperes per square metre. The Boltzmann constant k has the value 8.62 × 10−5 electron volts per kelvin, and temperature T is in kelvins. The constant A is 1.2 × 106 ampere degree squared per square metre, and varies slightly for different metals. For tungsten, which has a work function W of 4.5 electron volts, the value of A is 7 × 105 amperes per square metre kelvin squared and the current density at T equaling 2,400 K is 0.14 ampere per square centimetre. J rises rapidly with temperature. If T is increased to 2,600 K, J rises to 0.9 ampere per square centimetre. Tungsten does not emit appreciably at 2,000 K or below (less than 0.05 milliampere per square centimetre) because its work function of 4.5 electron volts is large compared to the thermal energy kT, which is only 0.16 electron volt. At 1,000 K, a mixture of barium and strontium oxides has a work function of approximately 1.3 electron volts and is a reasonably good conductor. Currents of several amperes per square centimetre can be drawn from such oxide cathodes, but in practice the current density is generally less than 0.2 ampere per square centimetre. The oxide layer deteriorates rapidly when higher current densities are drawn.
Secondary Electron Emission:
If electrons with energies of 10 to 1,000 electron volts strike a metal surface in a vacuum, their energy is lost in collisions in a region near the surface, and most of it is transferred to other electrons in the metal. Because this occurs near the surface, some of these electrons may be ejected from the metal and form a secondary emission current. The ratio of secondary electrons to incident electrons is known as the secondary emission coefficient. For low-incident energies (below about one electron volt), the primary electrons tend to be reflected and the secondary emission coefficient is near unity. With increasing energy, the coefficient at first falls and then at about 10 electron volts begins to rise again, usually reaching a peak of value between 2 and 4 at energies of a few hundred electron volts. At higher energies, the primary electrons penetrate so far below the surface before losing energy that the excited electrons have little chance of reaching the surface and escaping. The secondary emission coefficients fall and, when the electrons have energies exceeding 20 kiloelectron volts, are usually well below unity. Secondary emission also can occur in insulators. Because many insulators have rather high secondary emission coefficients, it is often useful when high secondary emission yields are required to coat a metal electrode with a thin insulator layer a few atoms thick.
Conductivity:
Photoelectric Conductivity:
If light with a photon energy hν that exceeds the work function W falls on a metal surface, some of the incident photons will transfer their energy to electrons, which then will be ejected from the metal. Since hν is greater than W, the excess energy hν − W transferred to the electrons will be observed as their kinetic energy outside the metal. The relation between electron kinetic energy E and the frequency ν (that is, E = hν − W) is known as the Einstein relation, and its experimental verification helped to establish the validity of quantum theory. The energy of the electrons depends on the frequency of the light, while the intensity of the light determines the rate of photoelectric emission.
In a semiconductor the valence band of energy levels is almost completely full while the conduction band is almost empty. The conductivity of the material derives from the few holes present in the valence band and the few electrons in the conduction band. Electrons can be excited from the valence to the conduction band by light photons having an energy hν that is larger than energy gap Eg between the bands. The process is an internal photoelectric effect. The value of Eg varies from semiconductor to semiconductor. For lead sulfide, the threshold frequency occurs in the infrared, whereas for zinc oxide it is in the ultraviolet. For silicon, Eg equals 1.1 electron volts, and the threshold wavelength is in the infrared, about 1,100 nanometres. Visible radiation produces electron transitions with almost unity quantum efficiency in silicon. Each transition yields a hole–electron pair (i.e., two carriers) that contributes to electric conductivity. For example, if one milliwatt of light strikes a sample of pure silicon in the form of a thin plate one square centimetre in area and 0.03 centimetre thick (which is thick enough to absorb all incident light), the resistance of the plate will be decreased by a factor of about 1,000. In practice, photoconductive effects are not usually as large as this, but this example indicates that appreciable changes in conductivity can occur even with low illumination. Photoconductive devices are simple to construct and are used to detect visible, infrared, and ultraviolet radiation.
Bio-electric Effects:
Bioelectricity refers to the generation or action of electric currents or voltages in biological processes. Bioelectric phenomena include fast signaling in nerves and the triggering of physical processes in muscles or glands. There is some similarity among the nerves, muscles, and glands of all organisms, possibly because fairly efficient electrochemical systems evolved early. Scientific studies tend to focus on the following: nerve or muscle tissue; such organs as the heart, brain, eye, ear, stomach, and certain glands; electric organs in some fish; and potentials associated with damaged tissue.
Electric activity in living tissue is a cellular phenomenon, dependent on the cell membrane. The membrane acts like a capacitor, storing energy as electrically charged ions on opposite sides of the membrane. The stored energy is available for rapid utilization and stabilizes the membrane system so that it is not activated by small disturbances.
Cells capable of electric activity show a resting potential in which their interiors are negative by about 0.1 volt or less compared with the outside of the cell. When the cell is activated, the resting potential may reverse suddenly in sign; as a result, the outside of the cell becomes negative and the inside positive. This condition lasts for a short time, after which the cell returns to its original resting state. This sequence, called depolarization and repolarization, is accompanied by a flow of substantial current through the active cell membrane, so that a “dipole-current source” exists for a short period. Small currents flow from this source through the aqueous medium containing the cell and are detectable at considerable distances from it. These currents, originating in active membrane, are functionally significant very close to their site of origin but must be considered incidental at any distance from it. In electric fish, however, adaptations have occurred, and this otherwise incidental electric current is actually utilized. In some species the external current is apparently used for sensing purposes, while in others it is used to stun or kill prey. In both cases, voltages from many cells add up in series, thus assuring that the specialized functions can be performed. Bioelectric potentials detected at some distance from the cells generating them may be as small as the 20 or 30 microvolts associated with certain components of the human electroencephalogram or the millivolt of the human electrocardiogram. On the other hand, electric eels can deliver electric shocks with voltages as large as 1,000 volts.
In addition to the potentials originating in nerve or muscle cells, relatively steady or slowly varying potentials (often designated dc) are known. These dc potentials occur in the following cases: in areas where cells have been damaged and where ionized potassium is leaking (as much as 50 millivolts); when one part of the brain is compared with another part (up to one millivolt); when different areas of the skin are compared (up to 10 millivolts); within pockets in active glands, e.g., follicles in the thyroid (as high as 60 millivolts); and in special structures in the inner ear (about 80 millivolts).
A small electric shock caused by static electricity during cold, dry weather is a familiar experience. While the sudden muscular reaction it engenders is sometimes unpleasant, it is usually harmless. Even though static potentials of several thousand volts are involved, a current exists for only a brief time and the total charge is very small. A steady current of two milliamperes through the body is barely noticeable. Severe electrical shock can occur above 10 milliamperes, however. Lethal current levels range from 100 to 200 milliamperes. Larger currents, which produce burns and unconsciousness, are not fatal if the victim is given prompt medical care. (Above 200 milliamperes, the heart is clamped during the shock and does not undergo ventricular fibrillation.) Prevention clearly includes avoiding contact with live electric wiring; risk of injury increases considerably if the skin is wet, as the electric resistance of wet skin may be hundreds of times smaller than that of dry skin.
|
210 videos|156 docs|94 tests
|

|
Explore Courses for Physics exam
|

|

















