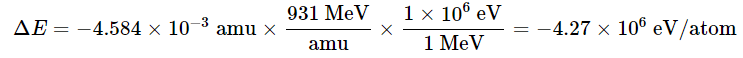Energy Changes in Nuclear Reactions | Chemistry for ACT PDF Download

Introduction

Nuclear reactions, similar to chemical reactions, involve energy transformations. However, the energy changes associated with nuclear reactions are significantly greater than those observed in even the most energetic chemical reactions. These substantial energy changes in nuclear reactions lead to measurable alterations in mass. In this section, we explore the connection between mass and energy in nuclear reactions and elucidate how even slight changes in mass during such reactions yield the release of tremendous amounts of energy.

Mass–Energy Balance

The relationship between mass (m) and energy (E) is expressed in the following equation: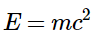

where

• c  is the speed of light ( 2.998 × 10⁸m/s), and
• E  and m  are expressed in units of joules and kilograms, respectively.

In 1905, Albert Einstein derived the relationship between mass and energy as part of his special theory of relativity. According to Equation E = mc², there is a direct proportionality between the mass of a particle and its energy. This means that every mass possesses a corresponding energy, and any reaction involving an energy change must also entail a change in mass. This presents a seeming contradiction with the law of conservation of mass. However, the solution to this paradox lies in the fact that while chemical reactions do result in changes in mass, these changes are typically too minuscule to be detectable. It is important to note that all particles exhibit wavelike behavior, with the wavelength being inversely proportional to the particle's mass (or more precisely, its momentum, which is the product of its mass and velocity). As a result, wavelike behavior is only observable in particles with very small masses, such as electrons. For instance, the chemical equation for the combustion of graphite to produce carbon dioxide can be expressed as follows: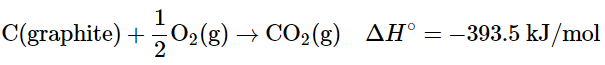

Combustion reactions are typically carried out at constant pressure, and under these conditions, the heat released or absorbed is equal to ΔH. When a reaction is carried out at constant volume, the heat released or absorbed is equal to ΔE. For most chemical reactions, however, ΔE ≈ ΔH. If we rewrite Einstein’s equation as: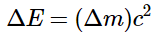

we can rearrange the equation to obtain the following relationship between the change in mass and the change in energy: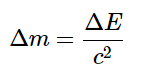
Because 1 J = 1 (kg•m²)/s², the change in mass is as follows: 
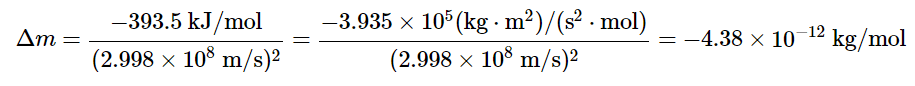This is a mass change of about 3.6 × 10⁻¹⁰ g/g carbon that is burned, or about 100-millionths of the mass of an electron per atom of carbon. In practice, this mass change is much too small to be measured experimentally and is negligible.
In contrast, for a typical nuclear reaction, such as the radioactive decay of ¹⁴C to ¹⁴N and an electron (a β particle), there is a much larger change in mass: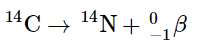
We can utilize the provided experimental masses of subatomic particles and common isotopes to directly compute the change in mass. The reaction involves the conversion of a neutral ¹⁴C atom into a positively charged ¹⁴N ion (with six, instead of seven, electrons) and a negatively charged β particle (an electron). Consequently, the mass of the products matches that of a neutral ¹⁴N atom. Therefore, the overall change in mass during the reaction corresponds to the disparity between the mass of a neutral ¹⁴N atom (14.003074 amu) and the mass of a ¹⁴C atom (14.003242 amu):
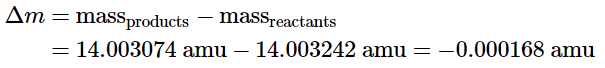The difference in mass, which has been released as energy, corresponds to almost one-third of an electron. The change in mass for the decay of 1 mol of ¹⁴C is −0.000168 g = −1.68 × 10⁻⁴ g = −1.68 × 10⁻⁷ kg. Although a mass change of this magnitude may seem small, it is about 1000 times larger than the mass change for the combustion of graphite. The energy change is as follows:

The energy released in this nuclear reaction is more than 100,000 times greater than that of a typical chemical reaction, even though the decay of ¹⁴C is a relatively low-energy nuclear reaction.
Because the energy changes in nuclear reactions are so large, they are often expressed in kiloelectronvolts (1 keV = 10³ eV), megaelectronvolts (1 MeV = 10⁶ eV), and even gigaelectronvolts (1 GeV = 10⁹ eV) per atom or particle. The change in energy that accompanies a nuclear reaction can be calculated from the change in mass using the relationship 1 amu = 931 MeV. The energy released by the decay of one atom of ¹⁴C is thus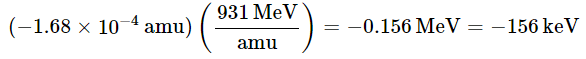

Example 1: Calculate the changes in mass (in atomic mass units) and energy (in joules per mole and electronvolts per atom) that accompany the radioactive decay of ²³⁸U to ²³⁴Th and an α particle. The α particle absorbs two electrons from the surrounding matter to form a helium atom.
Given: nuclear decay reaction
Asked for: changes in mass and energy
Strategy:
A. Use the mass values to calculate the change in mass for the decay reaction in atomic mass units.
B. Use Equation 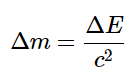  to calculate the change in energy in joules per mole.
C. Use the relationship between atomic mass units and megaelectronvolts to calculate the change in energy in electronvolts per atom.

A. Using particle and isotope masses, we can calculate the change in mass as follows:
B. Thus the change in mass for 1 mol of ²³⁸U is −0.004584 g or −4.584 × 10⁻⁶ kg. The change in energy in joules per mole is as follows:
C. The change in energy in electronvolts per atom is as follows:

Example 2: Calculate the changes in mass (in atomic mass units) and energy (in kilojoules per mole and kiloelectronvolts per atom) that accompany the radioactive decay of tritium (³H) to ³He and a β particle.

Δm = −2.0 × 10⁻⁵ amu; ΔE = −1.9 × 10⁶ kJ/mol = −19 keV/atom

Nuclear Binding Energies

We have observed that changes in energy during chemical and nuclear reactions are accompanied by corresponding changes in mass. Einstein's equation, which provides a relationship between mass and energy, leads to an intriguing implication: The mass of an atom is always lower than the combined masses of its individual particles. The sole exception to this principle is hydrogen-1 (¹H), where its measured mass of 1.007825 amu coincides with the sum of the masses of a proton and an electron. Conversely, the experimentally determined mass of a deuterium atom (²H) is 2.014102 amu, deviating from its calculated mass of 2.016490 amu: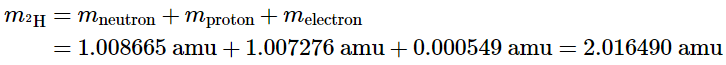
The discrepancy between the sum of the component masses and the actual measured atomic mass is referred to as the mass defect of the nucleus. Similar to how a molecule is more stable than its individual atoms, a nucleus is also more stable, meaning it has lower energy, compared to its isolated constituent particles. As a result, when individual nucleons come together to form a stable nucleus, energy is released. In accordance with Equation 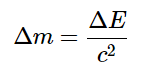, this energy release is accompanied by a decrease in the mass of the nucleus.
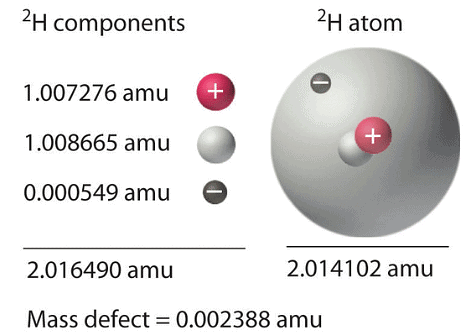Figure 1: Nuclear Binding Energy in Deuterium: The mass of a 2H atom is less than the sum of the masses of a proton, a neutron, and an electron by 0.002388 amu; the difference in mass corresponds to the nuclear binding energy. The larger the value of the mass defect, the greater the nuclear binding energy and the more stable the nucleus.
The nuclear binding energy, as depicted in Figure 1, represents the energy that is released when a nucleus is formed by combining its individual nucleons. For deuterium, the mass defect is measured to be 0.002388 amu, which corresponds to a nuclear binding energy of 2.22 MeV for the deuterium nucleus. Both the magnitude of the mass defect and the nuclear binding energy serve as indicators of the stability of the nucleus, with larger values indicating greater stability.

Just as a molecule is more stable (lower in energy) than its isolated atoms, a nucleus is more stable than its isolated components.

The relative stability of different nuclei can be described by chemists through the comparison of binding energy per nucleon. This value is obtained by dividing the nuclear binding energy by the mass number (A) of the nucleus. Figure 2 illustrates that the binding energy per nucleon shows a rapid increase as the atomic number (Z) increases, until approximately Z = 26. After that point, it levels off to around 8-9 MeV per nucleon and then gradually decreases. The initial increase in binding energy is not a smooth curve but rather displays distinct peaks corresponding to light nuclei that possess an equal number of protons and neutrons, such as ⁴He, ¹²C, and ¹⁶O. These combinations are particularly known for their stability.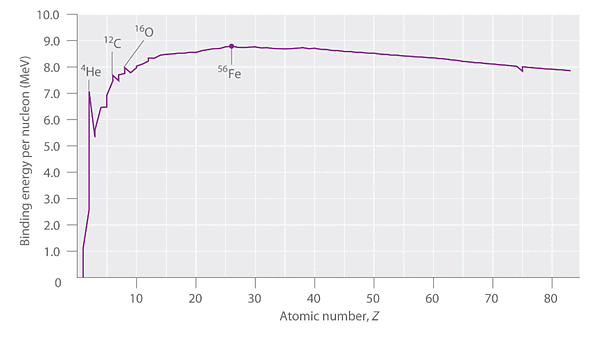

Figure  2: The Curve of Nuclear Binding Energy: This plot of the average binding energy per nucleon as a function of atomic number shows that the binding energy per nucleon increases with increasing atomic number until about Z = 26, levels off, and then decreases. The sharp peaks correspond to light nuclei that have equal numbers of protons and neutrons.

At ⁵⁶Fe, the maximum binding energy per nucleon is attained, making all other nuclei energetically unfavorable compared to the formation of ⁵⁶Fe. As a result, heavier nuclei (located towards the right in Figure 2) are expected to undergo spontaneous reactions, such as alpha decay, which lead to a decrease in atomic number. Conversely, lighter elements (situated on the left in Figure 2) should undergo reactions that result in an increase in atomic number. This pattern aligns with the observations made in nuclear reactions.

Heavier nuclei spontaneously undergo nuclear reactions that decrease their atomic number. Lighter nuclei spontaneously undergo nuclear reactions that increase their atomic number.

Example 3: Calculate the total nuclear binding energy (in megaelectronvolts) and the binding energy per nucleon for ⁵⁶Fe. The experimental mass of the nuclide is:

Given: nuclide and mass
Asked for: nuclear binding energy and binding energy per nucleon
Strategy:
A. Sum the masses of the protons, electrons, and neutrons or, alternatively, use the mass of the appropriate number of 1H atoms (because its mass is the same as the mass of one electron and one proton).
B. Calculate the mass defect by subtracting the experimental mass from the calculated mass.
C. Determine the nuclear binding energy by multiplying the mass defect by the change in energy in electronvolts per atom. Divide this value by the number of nucleons to obtain the binding energy per nucleon.

A. An iron-56 atom has 26 protons, 26 electrons, and 30 neutrons. We could add the masses of these three sets of particles; however, noting that 26 protons and 26 electrons are equivalent to 26 1H atoms, we can calculate the sum of the masses more quickly as follows:
calculated mass = 26(mass ¹₁H) + 30(mass ¹₀n)
= 26(1.007825)amu + 30(1.008665)amu = 56.463400 amu
experimental mass = 55.934938
B. We subtract to find the mass defect:
mass defect = calculated mass − experimental mass
= 56.463400 amu − 55.934938 amu = 0.528462 amu
C. The nuclear binding energy is thus 0.528462 amu × 931 MeV/amu = 492 MeV. The binding energy per nucleon is 492 MeV/56 nucleons = 8.79 MeV/nucleon.

Example 4: Calculate the total nuclear binding energy (in megaelectronvolts) and the binding energy per nucleon for 238U.

1800 MeV/²³⁸U; 7.57 MeV/nucleon

Summary

Unlike chemical reactions, nuclear reactions exhibit a significant alteration in mass, accompanied by a corresponding change in energy as elucidated by Einstein's equation. The energy transformations in nuclear reactions are substantial, leading to detectable modifications in mass. The relationship between the change in mass and the change in energy is governed by Einstein's equation: ΔE = (Δm)c². These considerable energy changes are typically expressed in kiloelectronvolts or megaelectronvolts (thousands or millions of electronvolts). Except for hydrogen-1 (¹H), the measured mass of an atom is consistently lower than the sum of the masses of its constituent particles (protons, neutrons, and electrons) by a quantity referred to as the mass defect of the nucleus. The nuclear binding energy is the energy associated with the mass defect, representing the energy released during the formation of a nucleus from its constituent particles. During nuclear fission, heavy nuclei divide into lighter nuclei, releasing a significant amount of energy along with multiple neutrons. The critical mass refers to the minimum mass necessary to sustain a self-perpetuating nuclear chain reaction. On the other hand, nuclear fusion involves the fusion of two light nuclei to form a heavier nucleus, accompanied by a substantial release of energy.