Energy Methods | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Strain Energy
The work done by the load in straining the body is stored within the strained material in the form of strain energy.
Strain energy,
U = 1 / 2 P(Al)
U = P2L / 2AE
Put
P = AEAℓ / L
Or
U = σ2 / 2E x V
 Strain Energy Diagram
Strain Energy Diagram
Proof Resilience
The maximum strain energy that can be stored in a material is known as proof resilience.

U = σ2 / 2E1
Where,
σ = p / A, u = 1 / 2 Ee2
Strain energy of prismatic bar with varying sections
 Prismatic bar
Prismatic bar

Ax = Cross-section of differential section.
 Non-Prismatic Bar
Non-Prismatic Bar
Stresses due to
(i) Gradual Loading: σ = F / A
(ii) Sudden Loading: σ = 2F / A
(iii) Impact Loading: Work done by falling weigth P is


Work stored in the bar
 .....(b)
.....(b)
By equating, stress will be

and If h is very small then

For solid shaft,
U = τ2 / 4G x Volume of Shaft
For hollow shaft, x Volume of Shaft
x Volume of Shaft
Castigliano’s First Theorem
It the strain energy of an elastic structure can be expressed as a function of generalized displacement, then the partial derivative of the strain energy with respect to generalized displacement gives the generalized force

[Where M is function of W (load)]
Deflection:
Slope:
Theories of failure are defined as following groups:
1. Maximum Principal Stress Theory (Rankine theory)- According to this theory, permanent set takes place under a state of complex stress, when the value of maximum principal stress is equal to that of yield point stress as found in a simple tensile test.
- For design, critical maximum principal stress (σ1) must not exceed the working stress (s1) for the material.
σ1 < σy
Note: For bittle material, it gives satisfactory result. Yield criteria for 3D stress system,
σ1 = σy or |σ3| = σry
Where, σy = Yield stress point in simple tension, and σy = Yield stress point in simple compression.
 Stresses on rectangular Section
Stresses on rectangular Section
2. Maximum Principal Strain Theory (St. Venant’s theory)
According to this theory, a ductile material begins to yield when the maximum principal strain at which yielding occurs in simple tension.
For 3D stress system,
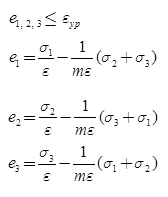
If ey = Yield point strain tensile σy / E
ery = Yield point strain compressive σry / E
According to theory, e1 = ey
Yield criteria: 
And 
For 2D system, 

 Rhombus
Rhombus
3. Maximum Shear Stress Theory (Guest & Tresca’s theory)Note: This theory can estimate the elastic strength of ductile material.
According to this theory, failure of specimen subjected to any combination of loads when the maximum shearing stress at any point reaches the failure value equal to that developed at the yielding in an axial tensile or compressive test of the same material.
For 3D system:
Yielding criteria,
τmax = 1 / 2 (σ1 - σ3) = σy / 2
In case of 2D: σ1 – σ3 = σy
Yielding criteria, σ1 - σ2 = σy
This theory gives well estimation for ductile material.
- According to this theory, a body under complex stress fails when the total strain energy on the body is equal to the strain energy at elastic limit in simple tension. For 3D stress system yield criteria,

For 2D stress system,

 EllipseThis theory does not apply to brittle material for which elastic limit stress in tension and in compression are different.
EllipseThis theory does not apply to brittle material for which elastic limit stress in tension and in compression are different.
- It states that inelastic action at any point in a body, under any combination of stress begins, when the strain energy of distortion per unit volume absorbed at the point is equal to the strain energy of distortion absorbed per unit volume at any point an a bar stressed to the elastic limit under the state of uniaxial stress as occurs in a simple tension/compression test.
1/2[(σ1 - σ2)2 + (σ1 - σ3)2 + (σ3 - σ1)2] ≤ σ2y For no failure
1/2[(σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2] ≤ (σy / FOS)2 For no failure
|
37 videos|39 docs|45 tests
|
FAQs on Energy Methods - Strength of Materials (SOM) - Mechanical Engineering
| 1. What are some energy methods used in the field of engineering? |  |
| 2. How does the Finite Element Method (FEM) work in energy analysis? |  |
| 3. What is the role of the Boundary Element Method (BEM) in energy analysis? |  |
| 4. How does the Finite Difference Method (FDM) contribute to energy analysis? |  |
| 5. What is the significance of the Rayleigh-Ritz Method in energy analysis? |  |

|
Explore Courses for Mechanical Engineering exam
|

|













