Energy and the Simple Harmonic Oscillator | Basic Physics for IIT JAM PDF Download
To study the energy of a simple harmonic oscillator, we first consider all the forms of energy it can have We know from Hooke’s Law: Stress and Strain Revisited that the energy stored in the deformation of a simple harmonic oscillator is a form of potential energy given by: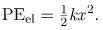
Because a simple harmonic oscillator has no dissipative forces, the other important form of energy is kinetic energy KE. Conservation of energy for these two forms is:
KE + PEel = constant
or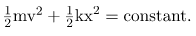
This statement of conservation of energy is valid for all simple harmonic oscillators, including ones where the gravitational force plays a role.
Namely, for a simple pendulum we replace the velocity with v =Lω, the spring constant with k = mg/L, and the displacement term with x = Lθ. Thus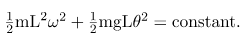
In the case of undamped simple harmonic motion, the energy oscillates back and forth between kinetic and potential, going completely from one to the other as the system oscillates. So for the simple example of an object on a frictionless surface attached to a spring, as shown again in, the motion starts with all of the energy stored in the spring. As the object starts to move, the elastic potential energy is converted to kinetic energy, becoming entirely kinetic energy at the equilibrium position. It is then converted back into elastic potential energy by the spring, the velocity becomes zero when the kinetic energy is completely converted, and so on. This concept provides extra insight here and in later applications of simple harmonic motion, such as alternating current circuits.
The transformation of energy in simple harmonic motion is illustrated for an object attached to a spring on a frictionless surface.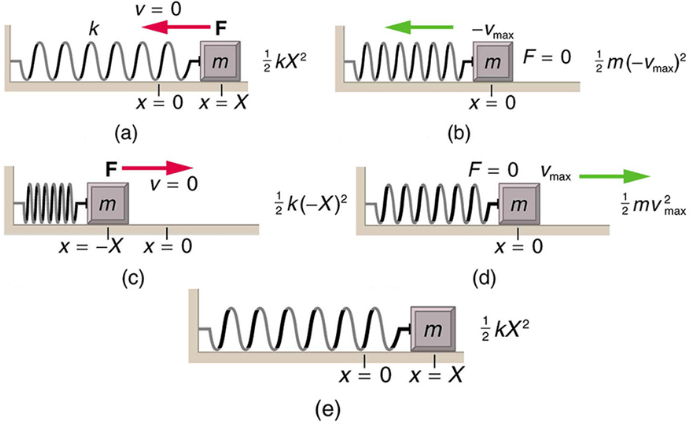
The conservation of energy principle can be used to derive an expression for velocity v. If we start our simple harmonic motion with zero velocity and maximum displacement (x=X), then the total energy is
1/2kX2.
This total energy is constant and is shifted back and forth between kinetic energy and potential energy, at most times being shared by each. The conservation of energy for this system in equation form is thus: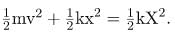
Solving this equation for v yields: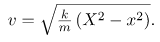
Manipulating this expression algebraically gives: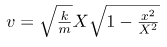
and so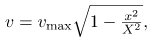
where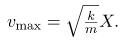
From this expression, we see that the velocity is a maximum (vmax) at x=0, as stated earlier in v(t) = -vmax sin 2πt/T. Notice that the maximum velocity depends on three factors. Maximum velocity is directly proportional to amplitude. As you might guess, the greater the maximum displacement the greater the maximum velocity. Maximum velocity is also greater for stiffer systems, because they exert greater force for the same displacement. This observation is seen in the expression for vmax; it is proportional to the square root of the force constant k. Finally, the maximum velocity is smaller for objects that have larger masses, because the maximum velocity is inversely proportional to the square root of m. For a given force, objects that have large masses accelerate more slowly.
A similar calculation for the simple pendulum produces a similar result, namely: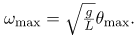
Determine the Maximum Speed of an Oscillating System: A Bumpy Road
Suppose that a car is 900 kg and has a suspension system that has a force constant k=6.53104 N/m. The car hits a bump and bounces with an amplitude of 0.100 m. What is its maximum vertical velocity if you assume no damping occurs?
Strategy
We can use the expression for vmax given in vmax = √k/m X to determine the maximum vertical velocity. The variables m and k are given in the problem statement, and the maximum displacement X is 0.100 m.
Solution
1. Identify known.
2. Substitute known values into 

3. Calculate to find vmax = 0.852 m/s.
Discussion
This answer seems reasonable for a bouncing car. There are other ways to use conservation of energy to find vmax. We could use it directly, as was done in the example featured in Hooke’s Law: Stress and Strain Revisited.
The small vertical displacement
y
of an oscillating simple pendulum, starting from its equilibrium position, is given as
y(t) = a sin ωt,
where a is the amplitude, ω is the angular velocity and t is the time taken. Substituting ω = 2π/T, we have
Thus, the displacement of pendulum is a function of time as shown above.
Also the velocity of the pendulum is given by
so the motion of the pendulum is a function of time.
Check Your Understanding
Why does it hurt more if your hand is snapped with a ruler than with a loose spring, even if the displacement of each system is equal?
The ruler is a stiffer system, which carries greater force for the same amount of displacement. The ruler snaps your hand with greater force, which hurts more.
Check Your Understanding
You are observing a simple harmonic oscillator. Identify one way you could decrease the maximum velocity of the system.
You could increase the mass of the object that is oscillating.
Section Summary
1. Energy in the simple harmonic oscillator is shared between elastic potential energy and kinetic energy, with the total being constant: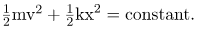
2. Maximum velocity depends on three factors: it is directly proportional to amplitude, it is greater for stiffer systems, and it is smaller for objects that have larger masses: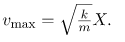
Conceptual Questions
Explain in terms of energy how dissipative forces such as friction reduce the amplitude of a harmonic oscillator. Also explain how a driving mechanism can compensate. (A pendulum clock is such a system.)
Problems & Exercises
The length of nylon rope from which a mountain climber is suspended has a force constant of 1.40104 N/m.
(a) What is the frequency at which he bounces, given his mass plus and the mass of his equipment are 90.0 kg?
(b) How much would this rope stretch to break the climber’s fall if he free-falls 2.00 m before the rope runs out of slack? Hint: Use conservation of energy.
(c) Repeat both parts of this problem in the situation where twice this length of nylon rope is used.
(a) 1.99 Hz.
(b) 50.2 cm
(c) 1.41 Hz, 0.710 m
Engineering Application
Near the top of the Citigroup Center building in New York City, there is an object with mass of 4.00105 kg on springs that have adjustable force constants. Its function is to dampen wind-driven oscillations of the building by oscillating at the same frequency as the building is being driven—the driving force is transferred to the object, which oscillates instead of the entire building. (a) What effective force constant should the springs have to make the object oscillate with a period of 2.00 s? (b) What energy is stored in the springs for a 2.00-m displacement from equilibrium?
(a) 3.95106 N/m
(b) 7.90106 J
|
210 videos|156 docs|94 tests
|

|
Explore Courses for Physics exam
|

|

















