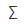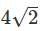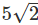Engesser Theorem & Truss Deflections by Virtual Work Principles - 1 | Structural Analysis - Civil Engineering (CE) PDF Download
Instructional Objectives
After reading this lesson, the reader will be able to:
1. State and prove Crotti-Engesser theorem.
2. Derive simple expressions for calculating deflections in trusses subjected to mechanical loading using unit-load method.
3. Derive equations for calculating deflections in trusses subjected to temperature loads.
4. Compute deflections in trusses using unit-load method due to fabrication errors.
Introduction
In the previous lesson, we discussed the principle of virtual work and principle of virtual displacement. Also, we derived unit – load method from the principle of virtual work and unit displacement method from the principle of virtual displacement. In this lesson, the unit load method is employed to calculate displacements of trusses due to external loading. Initially the Engesser’s theorem, which is more general than the Castigliano’s theorem, is discussed. In the end, few examples are solved to demonstrate the power of virtual work.
Crotti-Engesser Theorem
The Crotti-Engesser theorem states that the first partial derivative of the complementary strain energy (U*) expressed in terms of applied forces Fj is equal to the corresponding displacement.
 (6.1)
(6.1)
For the case of indeterminate structures this may be stated as,
 (6.2)
(6.2)
Note that Engesser’s theorem is valid for both linear and non-linear structures. When the complementary strain energy is equal to the strain energy (i.e. in case of linear structures) the equation (6.1) is nothing but the statement of Castigliano’s first theorem in terms of complementary strain energy.

In the above figure the strain energy (area OACO) is not equal to complementary strain energy (area OABO)
 (6.3)
(6.3)
Differentiating strain energy with respect to displacement,
dU/du = F (6.4)
This is the statement of Castigliano’s second theorem. Now the complementary energy is equal to the area enclosed by OABO.
 (6.5)
(6.5)
Differentiating complementary strain energy with respect to force F,
 (6.6)
(6.6)
This gives deflection in the direction of load. When the load displacement relationship is linear, the above equation coincides with the Castigliano’s first theorem given in equation (3.8).
Unit Load Method as applied to Trusses
External Loading
In case of a plane or a space truss, the only internal forces present are axial as the external loads are applied at joints. Hence, equation (5.7) may be written as,
 (6.7)
(6.7)
wherein, δFj is the external virtual load, uj are the actual deflections of the truss, δPv is the virtual stress resultant in the frame due to the virtual load and  is the actual internal deformation of the frame due to real forces. In the above equation L, , E A respectively represent length of the member, cross-sectional area of a member and modulus of elasticity of a member. In the unit load method, δFj = 1 and all other components of virtual forces
is the actual internal deformation of the frame due to real forces. In the above equation L, , E A respectively represent length of the member, cross-sectional area of a member and modulus of elasticity of a member. In the unit load method, δFj = 1 and all other components of virtual forces  are zero. Also, if the cross sectional area A of truss remains constant throughout, then integration may be replaced by summation and hence equation (6.7) may be written as,
are zero. Also, if the cross sectional area A of truss remains constant throughout, then integration may be replaced by summation and hence equation (6.7) may be written as,
 (6.8)
(6.8)
where m is the number of members, (δPv) is the internal virtual axial force in member i due to unit virtual load at j and  is the total deformation of memberi due to real loads. If we represent total deformation by Δi ,then
is the total deformation of memberi due to real loads. If we represent total deformation by Δi ,then
 (6.9)
(6.9)
where, Δi is the true change in length of member i due to real loads.
Temperature Loading
Due to change in the environmental temperature, the truss members either expand or shrink. This in turn produces joint deflections in the truss. This may be calculated by equation (6.9). In this case, the change in length of member Δi is calculated from the relation,
Δi = αTLi (6.10)
where α is the co-efficient of thermal expansion member, Li is the length of member and T is the temperature change.
Fabrication Errors and Camber
Sometimes, there will be errors in fabricating truss members. In some cases, the truss members are fabricated slightly longer or shorter in order to provide camber to the truss. Usually camber is provided in bridge truss so that its bottom chord is curved upward by an equal to its downward deflection of the chord when subjected to dead. In such instances, also, the truss joint deflection is calculated by equation (6.9). Here,
Δi = ei (6.11)
where, ei is the fabrication error in the length of the member. ei is taken as positive when the member lengths are fabricated slightly more than the actual length otherwise it is taken as negative.
Procedure for calculating truss deflection
1. First, calculate the real forces in the member of the truss either by method of joints or by method of sections due to the externally applied forces. From this determine the actual deformation (Δi) in each member from the equation 
Assume tensile forces as positive and compressive forces as negative.
2. Now, consider the virtual load system such that only a unit load is considered at the joint either in the horizontal or in the vertical direction, where the deflection is sought. Calculate virtual forces (δPv)ij in each member due to the applied unit load at the j-th joint.
3. Now, using equation (6.9), evaluate the j-th joint deflection uj.
4. If deflection of a joint needs to be calculated due to temperature change, then determine the actual deformation (Δi) in each member from the equation Δi = αTLi .
The application of equation (6.8) is shown with the help of few problems.
Example 6.1 Find horizontal and vertical deflection of joint C of truss ABCD loaded as shown in Fig. 6.2a. Assume that, all members have the same axial rigidity.


The given truss is statically determinate one. The reactions are as shown in Fig 6.2b along with member forces which are determined by equations of static equilibrium. To evaluate horizontal deflection at ‘C’, apply a unit load as shown in Fig 6.2c and evaluate the virtual forces δPv in each member. The magnitudes of internal forces are also shown in the respective figures. The tensile forces are shown as +ve and compressive forces are shown as –ve. At each end of the bar, arrows have been drawn indicating the direction in which the force in the member acts on the joint.


Horizontal deflection at joint C is calculated with the help of unit load method. This may be stated as,
 (1)
(1)
For calculating horizontal deflection at C, uc, apply a unit load at the joint C as shown in Fig.6.2c. The whole calculations are shown in table 6.1. The calculations are self explanatory.
Table 6.1 Computational details for horizontal deflection at C
Member | Length | L / AE | P | (P ), | (PPA EA |
units | m | m/kN | kN | kN | kN.m |
AB | 4 | 4/AE | 0 | 0 | 0 |
BC | 4 | 4/AE | 0 | 0 | 0 |
CD | 4 | 4/AE | -15 | -1 | 60/AE |
DA | 4 | 4/AE | 0 | 0 | 0 |
AC |
|
|
|
|
|
|
|
|
|
|
|
 (2)
(2)
Vertical deflection at joint C
 (3)
(3)
In this case, a unit vertical load is applied at joint C of the truss as shown in Fig. 6.2d.
Table 6.2 Computational details for vertical deflection at C
Member | Length | L / AE | P | (Pv), | (P )tPLt EA |
units | m | m/kN | kN | kN | kN.m |
AB | 4 | 4/AE | 0 | 0 | 0 |
BC | 4 | 4/AE | 0 | 0 | 0 |
CD | 4 | 4/AE | -15 | -1 | 60/AE |
DA | 4 | 4/AE | 0 | 0 | 0 |
AC |
|
|
| 0 | 0 |
|
|
|
|
| 60/AE |
 (4)
(4)
|
34 videos|140 docs|31 tests
|
FAQs on Engesser Theorem & Truss Deflections by Virtual Work Principles - 1 - Structural Analysis - Civil Engineering (CE)
| 1. What is Engesser's Theorem? |  |
| 2. How does Engesser's Theorem help in calculating truss deflections? |  |
| 3. What are the virtual work principles used in truss deflection calculations? |  |
| 4. How can Engesser's Theorem be applied practically in civil engineering projects? |  |
| 5. Are there any limitations or assumptions associated with Engesser's Theorem? |  |

|
Explore Courses for Civil Engineering (CE) exam
|

|
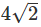
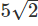
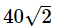 /AE
/AE