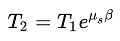Engineering Mechanics | Mechanical Engineering SSC JE (Technical) PDF Download
Fundamental Laws of Newtonian Mechanics
1. Newton's 3 laws
-Newton's first law states that every body continues in its state of rest or of uniform motion in a straight line unless it is compelled by an external agency.
-According to Newton's second law
Force µ Mass × Acceleration
-Newton's third law states action and reaction is equal and opposite
2. Law of gravitation
According to Newton's law of gravitational acceleration the force of attraction between the bodies of mass m1 and mass m2 at a distance d is
where G is the constant of proportionality
3. Law of transmissibility of forces
According to the law of transmissibility of force, the state of rest or motion of the rigid body is unaltered, if a force acting on the body is replaced by another force of the same magnitude and direction but acting at any other point on the body along the line of action of the replaced force.
4. Parallelogram law of forces
Parallelogram law of forces states that if two forces acting simultaneously on a body at a point are represented in magnitude and direction by the two adjacent sides of a parallelogram, their resultant is represented in magnitude and direction by the diagonal of the parallelogram which passes through the point of intersection of the two sides representing the forces.
- Triangle law of forces and polygon law of forces are the laws derived form parallelogram law of forces.
- Unit of force is so defined that the constant of proportionality in Newton's second law becomes unity. In SI system I newton of force moves I kg mass at an acceleration of 1m/ sec2.
- 1 kg – wt = 9.81 newton. In practice 1 kg-wt is simply called 1 kg.
System of forces
1. If all forces do not lie in a single plane, it is system or forces in space. If all forces lie in a single plane it is coplanar force system.
2. If all forces in a system pass through a single point it is concurrent force system otherwise it is non-concurrent force system.
3. If all forces in a system are parallel to each other it is parallel force system.
Scalars and Vectors
A quantity is said to be scalar, if it is completely defined by its magnitude alone and it is vector, if it is completely defined only when its magnitude as well as directions are specified.
Resultant And Equilibrium of System of Coplanar Concurrent Forces
- If F1 and F2 are two forces acting on a particle and the angle between them is q, the magnitude of their resultant is

and the inclination of resultant to the direction of force F1 is

- If a force F makes angle q with x - direction,

- If a system of forces are acting on a particle,
R = √[(ΔFx)2 + (ΔFy)2]
and its inclination to x-axis a is given by
a = tan-1(ΔFy/ΔFx)
- Self-weight (W = mg) and reactions from the bodies in contact with the body under consideration are non-applied forces.
- If body under consideration is freed from contact surfaces of other bodies and the forces on it including self - weight and reactions from contact surface is shown, it is known as free body diagram (FBD) of the body.
- Lami's theorem states that if a body is in equilibrium under the action of only three forces, each force is proportional to the sine of the angle between the other two forces.

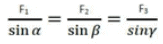
- If contact surfaces are smooth, reaction between them is normal to the tangent at contact surfaces.
- Equilibrium equations in planar system are,
ΔFx = 0, ΔFy = 0
Resultant and Equilibrium of Coplanar Non-Concurrent Forces
- Moment of a force about a point is the measure of rotational effect of the force and is given by
M = F × d
where F = the force and d is perpendicular distance of the force from the moment centre. - Varignon's theorem, also known as principle of moments, states the algebraic sum of moments of a system of coplanar forces about a moment centre is equal to the moment of their resultant force about the same moment centre.
R * d = ΔFidi
- Two parallel forces equal in magnitude and opposite in direction and separated by a definite distance are said to form a couple.
1. The translatory effect of a couple on the body is zero.
2. The rotational effect about any point is a constant. - Magnitude, direction and the distance of resultant force from the moment centre are given by
R = [(ΔFx)2 + (ΔFy)2]1/2
a = tan-1(ΔFy/ΔFx)
d = ΔMo/R
- x and y intercepts of resultant of non- concurrent system of forces in plane are
x = ΔMo/Ry , y = ΔMo/Rx - Equations of equilibrium of non-concurrent system of forces are
Rx = ΔFx = 0, Ry = ΔFy = 0, ΔMA = 0
If points A, B and C are not collinear, the following equations of equilibrium may also be used:
ΔFA = 0, ΔMB = 0, ΔMC = 0
If line AB is not in y-direction, the following set of equilibrium equations may be used
Ry = ΔFy = 0, ΔMB = 0, ΔMC = 0
BEAMS
- A beam is a structural element which has one dimension (length) considerably large than the other two dimensions in the cross section and is supported at a few points.
- Types of supports: Simple supports, roller supports – hinged support and fixed supports.
Types of Beams:
1. Determinate Beams: cantilever, simply supported, one end hinged and other on roller, overhanging.
2. Indeterminate Beams: both ends hinged, proper cantilever, continuous.
Statically determinate beams are the beams, in which all reaction components at supports can be found using the equations of equilibrium only.
Types of Loadings: Concentrated load, uniformly distributed load (UDL), uniformly varying load (UVL) general loading, external moments.
Analysis of Pin-Jointed Plane Frames
- A pin-jointed frame is a structure made of slender members pin connected at ends and capable of taking loads at joints.
- A perfect frame is the one which retains its shape with minimum number of members and can carry loads applied at joints
- A frame is said to be deficient, if the number of members in it are less than that required for a perfect frame.
- A frame is said to be redundant, if the number of members in it are more than that required for a perfect frame.
- The assumptions made in the analysis of pin-jointed frames are:
1. The ends of members are pin-connected.
2. The loads act at joints only.
3. Self weight is negligible.
4. If there are a number of members along a line of truss, they are located along the same longitudinal line.
FRICTION
- Friction is the resistance to motion offered by minutely projecting particles at the contact surfaces.
- The limiting value of frictional force when the motion is impending, is known as limiting friction upto this state it is static friction.
- The friction experienced by a body while in motion is known as dynamic friction. It may be sliding friction or rolling friction.
- The ratio of limiting friction to normal reaction is known as coefficient of friction.

- Coulomb’s laws of friction:
1. Friction always opposes motion
2. Till the limiting value is reached, the magnitude of friction is exactly equal to the force which tends to move the body.
3. Coefficient of friction for two contacting surface is constant.
4. Frictional force depends upon the roughness of the surfaces in contact.
5. Force of friction does not depend upon the area of contact.
6. Coefficient of dynamic friction is less than coefficient of static friction.
- The angle of limiting friction is the angle between the resultant reaction and the normal to the horizontal plane on which the motion of the body is impending.
- The maximum inclination of the plane on which a body, free from external forces, can repose (sleep) is called angle of repose.
- The inverted cone with semi-central angle a equal to limiting angle of friction is called as cone of friction.
- Rope/belt friction:

where, T1 = force on slack side
T2 = force on tight side
μs = coefficient of friction
β= angle of contact
1.The forces must be parallel to each other.
2.The forces must not lie in a single plane.
3.The forces must be concurrent.
4.The forces must have equal magnitudes.
How many statement are incorrect
Law of Machine
P=mW+C where
P = effort, W = load C = constant,
m = tan q, the slope of line AB in the effort vs load diagram.
Load- This is the resistance to be overcome by the machine.
Effort- This is the force required to overcome resistance.
Mechanical advantage = 
Velocity ratio = 
Input It is work done by effort = P×D
Output Useful work got out of the machine = Wd.

Ideal machine :m = 1, i.e., MA= velocity ratio.
Ideal effort :Effort required by ideal machine

Ideal Load :Load that can be lifted by ideal machine

Reversibility of a machine :If the removal of effort while lifting results in lowering of the load, the machine is said to be reversible. It can be shown that a lifting machine is reversible, if its efficiency is more than 50 per cent and is self-locking if r < 50%
- Velocity Ratio(VR)
In the first order pulley system VR = 2n
In the second order pulley system VR = 2n
In the third order pulley system VR = 2n-1
where n is the number of pulleys in the system.
- In wheel and axle,

where D = diameter of wheel d and d = diameter of axle
- In wheel and differential axle,

where D = diameter of effort wheel
d1 = diameter of larger axle
d2 = diameter of smaller axle
- In case of Weston differential pulley block,


where D = diameter of larger block d = diameter of smaller wheel of the block
- In case of inclined plane,

where q is the inclination of plane to horizontal.
- In case of screw jack, while ascending.

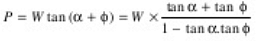
where,
P= Effort applied at the mean radius to lift the load
W= Weight of the body to be lifted
μ= Coefficient of friction, between the screw and nut
ϕ= Angle of friction,
while descending,
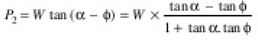
- In case of differential jack,

where R = length of effort arm
PA = pitch of outer screw, PB = pitch of inner screw
- Velocity ratio of winch crab is given by
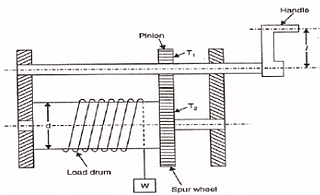

where R = length of lever arm T1 = number of teeth on pinion T2 = number of teeth on spur wheel.
- In case of double purchases winch crab
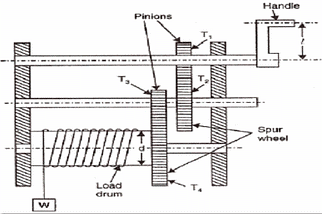
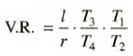
where l = length of lever arm T1,T2, T3, T4 are teeth on wheels 1 to 4 respectively.
Virtual Work Method
- The work done is virtual if the displacements are virtual or forces acting are virtual.
- Virtual work method consists of:
1. Give an elemental virtual displacement
2. Find work done by each force in the system
3. Equate total work done to zero. - Many times these equations are identical to the equation of equilibrium.
Centroid and Moment of Inertia - The term centroid applies to the plane areas and the term centre of gravity applies to the bodies with mass and weight.
- Centre of gravity of a body is the point through which the resultant gravitational force acts.
- Centroid is a point in a plane area such that the moment of area about any axis through that point is zero.
- Centroid lies on the axis of symmetry, if it exists.
- The distance of centroid from an axis is given by
Ý= ∫(ydA)/A
where y is distance of the element from the axis.
- Centroid of composite figures may be found by
Ý= Δaiyi/Δai
where ai = area of ith simple figure
yi = distance of the centroid of rth simple figure.
If r is the distance of elemental area dA form the axis AB, the sum of the terms å r 2dA to cover entire area is called moment of inertia of the area about the axis AB.
Iab = Δr2dA = ∫r2dA
- Moment of inertia about an axis perpendicular to the plane of area is known as polar moment of inertia.
- Radius of gyration k is given by

where I = moment of inertia A = area of the cross section. i.e., Ak2 = I
- Perpendicular axis theorem states, ‘the moment of inertia’ of an area about an axis perpendicular to its plane at any point O, is equal to the sum of moments of inertia about any two mutually perpendicular axes through the same point O and lying in the plane’ of the area,
Izz = Ixx + Iyy. - Parallel axis theorem states, ‘moment of inertia about any axis in the plane of the area is equal to the sum of moment of inertia about a parallel centroidal axis and the product of area and square of the distance between the two parallel axes.’

Moment of inertia of composite figures = sum of moment of inertia of all simple figures about the axis referred.
Centre of Gravity And Mass Moment of Inertia

- Centre of gravity of right circular cone of base radius r and height h is at a distance
 h from apex.
h from apex.
- Centre of gravity of solid hemisphere of radius r from its diametral axis is at

- Pappus-Guildinus Theorem-I: The area of surface generated by revolving a plane curve about a non-intersecting axis in the plane of the curve is equal to the length of the curve times the distance travelled by the centroid of the curve in a revolution.
- Pappus-Guildinus Theorem-II: The volume of the solid generated by revolving a plane area about a non-intersecting axis in the plane is equal to the area of the generating plane times the distance travelled by the centroid of the plane area during a revolution.
- Mass moment of inertia of a body about an axis is the sum total of product of its elemental masses and square of their distance from the axis.
Iab = Δr2dm = ∫r2dm
The unit of mass moment of inertia works out to be N-m-sec2. - Radius of gyration of a body is that distance which when squared and multiplied with total mass of the body gives the mass moment of inertia of the body.

- Mass moment of inertia of a uniform rod of length L and mass M about an axis normal to it at its centroidal axis is

and about one end is
- Mass moment of inertia of a rectangular plate of size ax b and uniform thickness, having total mass M about its centroidal axis is

- Mass moments of inertia of a circular ring of radius R and uniform cross section about a diametral axis is

- Mass moment of inertia of a solid cone of height h and base radius R
(a) about its axis of rotation
(b) about an axis through vertex and normal to the axis of rotation
Iyy =
- Mass moment of inertia of a solid plate of radius R about its diametral axis

Dyanamics
- A body is said to be in motion, if it is changing its position with respect to a reference point.
- Distance and speed are scalars while displacement and velocity are vectors.
- A motion is said to be translation, if a straight line drawn on the moving body remains parallel to its original position at any time.
- During translation, if the path traced by a point is a straight line, it is called rectilinear translation and if it is curved, it is called curvilinear translation.
- General plane motion is a combination of both translation and rotation.
- If s is displacement, v is velocity and a is acceleration,

- If velocity is uniform a = 0, and s = vt.
- In case of motion with uniform acceleration,
if u - initial velocity, v - final velocity
t - time
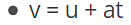
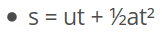
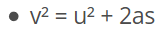
- In case of motion with varying acceleration,

Projectile Motion
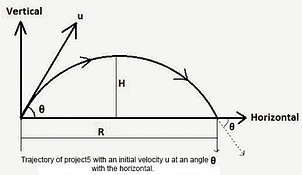
If, u = velocity of projection, a = angle of projection
1. The trajectory is a parabola
2. Maximum height reached
3. Time required to reach maximum height
4. Time of flight =
5. Horizontal range R =
6. Maximum range is when a = 45°
7. Range is the same when
Relative velocity
Relative velocity of A with respect to B is the vector difference between the velocities of A and B.
VA/B= VA–VB
Resultant velocity It is the vector sum of the velocities caused by different forces acting on a body.
D’AI emberts Principle It states that the system of forces acting on a body in motion is in dynamic equilibrium with the inertia force R – ma = 0
The term '– ma’ is known as inertia force or reverse effective force.
- When a lift is moving downward, with acceleration a
R = W(1–a/g) - When a lift is moving upward, with acceleration a
R = W(1+a/g)
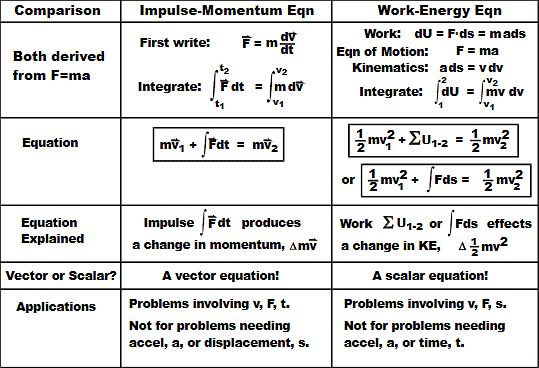
WORK ENERGY METHOD
- Work done by a force on a moving body is the product of the force and the distance moved by the body in the direction of the force.
- Energy is defined as the capacity to do work.
- Unit of energy and unit of work done are the same, i.e., joules.
1 joule = 1 N-m - Power is defined as rate of doing work. Unit of power is watt.
1 watt = 1 N-m/sec. - Work-energy equation states
Work done = Final K.E - Initial K.E. i.e.,
the work done by a system of forces acting on a body during a displacement is equal to the change in kinetic energy of the body during the same displacement. - Work-energy equation will be more suited if the interest is to find velocity and distance.
- Work done by a spring of stiffness k is 1/2 kx2
where x is distance from normal position of spring.
Impulse Momentum
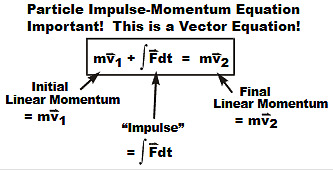
- The impulse momentum equation may be stated as the component of the resultant linear impulse along any direction is equal to the change in the component of momentum in that direction.
- The impulse-momentum (I-M) equation is a reformulation and integrated form, like the work-energy equation- of the equation of motion, F= ma.
- Impulse momentum method is more useful in solving problems involving force, time and velocity.
- The principle of conservation of momentum may be stated as ‘the momentum is conserved in a system in which resultant force is zero. In other words, if the resultant force is zero, the initial momentum will remain equal to the final momentum.
Impact of Elastic Bodies
- A collision between two bodies is said to be impact, if the bodies are in contact for a short interval of time and exert very large force on each other during this short period.
- Common normal to the colliding surface of the two bodies is known as line of impact.
- If the motion of the two colliding bodies is directed along the line of impact, the impact is said to be a direct impact.
- If the motion of one or both bodies is not directed along the line of impact, the impact is known as oblique impact.
- If the mass centres of colliding bodies are on the line of impact, the impact is called central impact.
- Even if mass centre of one of the colliding bodies is not on the line of impact, the impact is called eccentric impact.
- Period of collision (i.e., time of impact) consists of period of deformation and period of restitution. 1 If u1 u2 are initial velocities and vb v2 are the final velocities of two colliding bodies along the line of impact, coefficient of restitution

Circular Motion of Rigid Bodies
- When a body moves with uniform velocity v along a curved path of radius r, it has a radical inward acceleration of magnitude v2/r.
- When a body moves with uniform velocity v along a curved path of radius r, it experiences centrifugal force of magnitude
 in radial outward direction.
in radial outward direction. - On a circular flat path of radius r, the limiting velocity of a vehicle is (√μgr) to avoid skidding where m is the coefficient of friction between the path and the wheels.
- If h is the height of centre of gravity of vehicle, to avoid overturning it should go at a speed of less than

where r = radius of curved path
B = distance between the wheels of an axle. - By providing camber/super elevation
1. Skidding and overturning can be avoided.
2. Higher speeds can be permitted.
3. Lateral pressure on wheels may be reduced.
4. Excess wear and tear of wheels can be avoided. - The speed on a banked path for which lateral pressure developed is zero is called the design speed on that curve.
Rotation of Rigid Bodies
S = rθ , vt = rdθ/dt , at = rd2θ/dt2
ω = rdθ/dt , α = d2θ/dt2 = ωdω/dθ
In case of uniform angular velocity.
q= wt
In case of uniformly accelerated angular motion,
the general equations of motions are:
- ωf = ωi + αt
- θ = ωit + 1/2αt2
- ωf2 - ωi2 = 2αθ
- Kinetics of Rigid Body Rotation
- Angular momentum = Iω
- K.E. = 1/2Iω2
- Mechanical Vibration
- If the disturbing force does not act during vibration, it is called free vibration. If disturbing force acts at periodical interval on the body, it is called forced vibration.
- Each repetition of motion is called a cycle.
- The time interval required to complete one cycle of vibration is called the period of vibration (T)
- The reciprocal of the period is called frequency
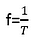
- A cycle per second is called one Hertz (Hz)
- The maximum displacement from the equilibrium position is called amplitude.
- A motion in which acceleration of the body is directly proportional to its displacement and is directed towards mean position is called simple harmonic motion (SHM). Thus, in SHM a = – kx/m.
- In case of simple pendulum,
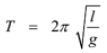
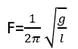
where, l is length of pendulum
g is the acceleration due to gravity
General Plane Motion of Rigid Bodies
- A body is said to have general plane motion, if it possesses translation and rotational motion simultaneously.
- For the analysis of general plane motion, it is convenient to split the motion into translational and pure rotation cases.
- At any instant of time it is possible to locate a point in the plane of the motion which has zero velocity and hence plane motion of the other points may be looked upon as pure rotation about this point. Such point is called instantaneous centre, and the axis passing through this point and at right angles to the plane of the motion is called instantaneous axis of rotation.
|
5 videos|103 docs|59 tests
|
FAQs on Engineering Mechanics - Mechanical Engineering SSC JE (Technical)
| 1. What are the fundamental principles of engineering mechanics? |  |
| 2. How is mechanical engineering related to engineering mechanics? |  |
| 3. What are some common applications of engineering mechanics in mechanical engineering? |  |
| 4. How does the study of engineering mechanics contribute to the field of mechanical engineering? |  |
| 5. What role does engineering mechanics play in the design and testing of mechanical systems? |  |
|
5 videos|103 docs|59 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|