Entropy and efficiency limits | Basic Physics for IIT JAM PDF Download
The concept of entropy was first introduced in 1850 by Clausius as a precise mathematical way of testing whether the second law of thermodynamics is violated by a particular process. The test begins with the definition that if an amount of heat Q flows into a heat reservoir at constant temperature T, then its entropy S increases by ΔS = Q/T. (This equation in effect provides a thermodynamic definition of temperature that can be shown to be identical to the conventional thermometric one.) Assume now that there are two heat reservoirs R1 and R2 at temperatures T1 and T2. If an amount of heat Q flows from R1 to R2, then the net entropy change for the two reservoirs is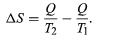
(3) ΔS is positive, provided that T1 > T2. Thus, the observation that heat never flows spontaneously from a colder region to a hotter region (the Clausius form of the second law of thermodynamics) is equivalent to requiring the net entropy change to be positive for a spontaneous flow of heat. If T1 = T2, then the reservoirs are in equilibrium and ΔS = 0.
The condition ΔS ≥ 0 determines the maximum possible efficiency of heat engines. Suppose that some system capable of doing work in a cyclic fashion (a heat engine) absorbs heat Q1 from R1 and exhausts heat Q2 to R2 for each complete cycle. Because the system returns to its original state at the end of a cycle, its energy does not change. Then, by conservation of energy, the work done per cycle is W = Q1 − Q2, and the net entropy change for the two reservoirs is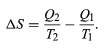 (4)
(4)
To make W as large as possible, Q2 should be kept as small as possible relative to Q1. However, Q2 cannot be zero, because this would make ΔS negative and so violate the second law of thermodynamics. The smallest possible value of Q2 corresponds to the condition ΔS = 0, yielding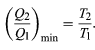 (5)
(5)
This is the fundamental equation limiting the efficiency of all heat engines whose function is to convert heat into work (such as electric power generators). The actual efficiency is defined to be the fraction of Q1 that is converted to work (W/Q1), which is equivalent to equation (2).
The maximum efficiency for a given T1 and T2 is thus
A process for which ΔS = 0 is said to be reversible because an infinitesimal change would be sufficient to make the heat engine run backward as a refrigerator.
As an example, the properties of materials limit the practical upper temperature for thermal power plants to T1 ≅ 1,200 K. Taking T2 to be the temperature of the environment (300 K), the maximum efficiency is 1 − 300/1,200 = 0.75. Thus, at least 25 percent of the heat energy produced must be exhausted into the environment as waste heat to avoid violating the second law of thermodynamics. Because of various imperfections, such as friction and imperfect thermal insulation, the actual efficiency of power plants seldom exceeds about 60 percent. However, because of the second law of thermodynamics, no amount of ingenuity or improvements in design can increase the efficiency beyond about 75 percent.
|
217 videos|156 docs|94 tests
|
FAQs on Entropy and efficiency limits - Basic Physics for IIT JAM
| 1. What is entropy and how is it related to efficiency limits? |  |
| 2. Can efficiency limits be surpassed in energy conversion processes? |  |
| 3. How does entropy affect the efficiency of energy conversion devices? |  |
| 4. Are there any strategies to increase the efficiency of energy conversion processes within the limits of entropy? |  |
| 5. How does the concept of entropy apply to renewable energy systems? |  |
















