Equation of Sphere | Mathematics for NDA PDF Download

Sphere

A sphere is defined as the path traced by a point moving in space, maintaining a constant distance from a fixed point known as the center, and this fixed distance is called the radius. It is created by rotating a circle around one of its parameters. The sphere shares many properties with a circle, but there are subtle distinctions.

Key Terminology:

• A diameter is a line segment connecting two points on a sphere, passing through the center.
• The geodesic is the shortest distance between any two points on a sphere.
• The surface area (A) of a sphere with radius 'r' is given by A = 4πr².
• The volume (V) of a sphere with radius 'r' is given by V = (4/3)πr³.

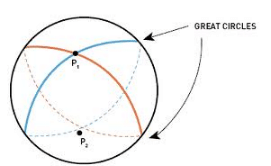
Great Circle:

A significant concept related to a sphere is the great circle, formed by the intersection of the sphere's surface with a plane passing through its center. Multiple great circles can satisfy specific criteria.

Equation of Sphere in Diverse Forms

Now we discuss the equation of sphere in various diverse forms:
The general equation of sphere with center at (a, b, c) and radius ‘r’ is given by
(x – a)² + (y – b)² + (z – c)² = r²
The same general equation in expanded form can be written as
x² + y² + z² + 2ux + 2vy + 2wz + d = 0
The center in this case becomes (–u, –v, –w),
And radius is given by r= √μ² + v² + w² – d. 

Remark:
If instead of (a, b, c), the centre is at origin i.e. (0, 0, 0) then the equation becomes x² + y² + z² = r².
In spherical coordinates, the points on the sphere can be written as
x = x₀ + r cos θ sin φ
y = y₀ + r cos θ sin φ
z = z₀ + r cos φ where 0 ≤ θ ≤ 2π and 0 ≤ φ ≤ π

Diameter form:
By the diameter form we mean the equation of the sphere when extremities of the diameter are given.
Equation of a sphere whose extremities of diameter are A (x₁, y₁, z₁) and B (x₂, y₂, z₂) is
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) + (z – z₁) (z – z₂) = 0.

Illustration:
Find the equation of the sphere which passes through the points (1, –3, 4), (1, –5, 2) and (1, –3, 0) and whose centre is on the plane x + y + z = 0.
Sol:
Let equation of the sphere be
x² + y² + z² + 2ux + 2vy + 2wz + d = 0
Its centre is (- u, - v, - w) which is on x + y + z = 0
⇒ u + v + w = 0                                                                  
It passes through (1, - 3, 4) ⇒ 2u - 6v + 8w + d = - 26       … (2)
(1, - 5, 2) ⇒ 2 u - 10 v + 4 w + d = - 30   … (3)
and it passes through (1, - 3, 0) ⇒2u - 6v + d = - 10  … (4)
Solving these four equations we get,
u = - 1, v = 3, w = - 2 and d = 10
Therefore required equation of the sphere is
x² + y² + z² - 2x + 6y - 4z + 10 = 0.  

Illustration:
Find the equation of the sphere whose centre is (2, –3, 4) and which passes through the point (1, 2, –1).
Sol:
We know that the radius of the sphere is
Radius of sphere = √{(2–1)² + (–3–2)² + (4+1)²} = √51
∴ Equation of the sphere is (x – 2)² + (y + 3)² + (z – 4)² = (√51)²
i.e. x² + y² + z² – 4x + 6y – 8z – 22 = 0.