Eulerian & Hamiltonian Graphs | Engineering Mathematics - Engineering Mathematics PDF Download
Aim
- To introduce Eulerian and Hamiltonian graphs.
Learning Outcomes
At the end of this section you will:
- Know what an Eulerian graph is,
- Know what a Hamiltonian graph is.
Eulerian Graphs
The following problem, often referred to as the bridges of K¨onigsberg problem, was first solved by Euler in the eighteenth century. The problem was rather simple — the town of K¨onigsberg consists of two islands and seven bridges. Is it possible, by beginning anywhere and ending anywhere, to walk through the town by crossing all seven bridges but not crossing any bridge twice?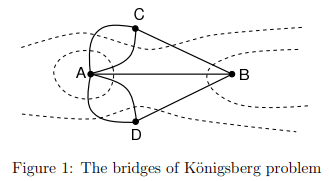
We will first present some definitions and then present a theorem that Euler used to show that it is in fact impossible to walk through the town and traverse all the bridges only once.
- Eulerian trail: An Eulerian trail is a trail that visits every edge of the graph once and only once. It can end on a vertex different from the one on which it began. A graph of this kind is said to be traversable.
- Eulerian Circuit: An Eulerian circuit is an Eulerian trail that is a circuit. That is, it begins and ends on the same vertex.
- Eulerian Graph: A graph is called Eulerian when it contains an Eulerian circuit.
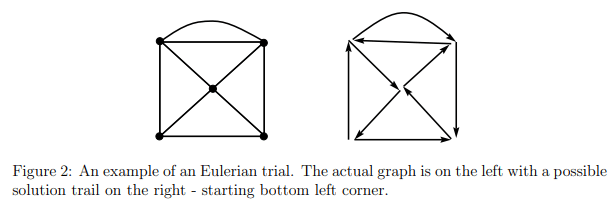 A vertex is odd if its degree is odd and even if its degree is even.
A vertex is odd if its degree is odd and even if its degree is even.
Theorem: An Eulerian trail exists in a connected graph if and only if there are either no odd vertices or two odd vertices.
For the case of no odd vertices, the path can begin at any vertex and will end there; for the case of two odd vertices, the path must begin at one odd vertex and end at the other. Any finite connected graph with two odd vertices is traversable. A traversable trail may begin at either odd vertex and will end at the other odd vertex.
Note: From this we can see that it is not possible to solve the bridges of K¨onisgberg problem because there exists within the graph more than 2 vertices of odd degree.
Question: Are either of the following graphs traversable - if so, graph the solution trail of the graph?

Hamiltonian Graphs
- Hamiltonian Circuit: A Hamiltonian circuit in a graph is a closed path that visits every vertex in the graph exactly once. (Such a closed loop must be a cycle.)
A Hamiltonian circuit ends up at the vertex from where it started.
Hamiltonian graphs are named after the nineteenth-century Irish mathematician Sir
William Rowan Hamilton(1805-1865). This type of problem is often referred to as the
traveling salesman or postman problem. - Hamiltonian Graph: If a graph has a Hamiltonian circuit, then the graph is called a Hamiltonian graph.
Important: An Eulerian circuit traverses every edge in a graph exactly once, but may repeat vertices, while a Hamiltonian circuit visits each vertex in a graph exactly once but may repeat edges.
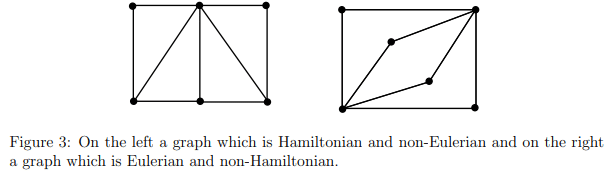
Question: Is the following graph Hamiltonian or Eulerian or both?
|
65 videos|129 docs|94 tests
|
















