NCERT Solutions for Class 10 Maths - Polynomials Exercise 2.3
Q1. Determine which of the following polynomials has (x + 1) a factor:
(i) x3 + x2 + x + 1
Ans: Let p(x) = x3 + x2 + x + 1
The zero of x + 1 is -1. [x + 1 = 0 means x = -1]
p(−1) = (−1)3 + (−1)2 + (−1) + 1
= −1 + 1 − 1 + 1
= 0
∴ By factor theorem, x + 1 is a factor of x3 + x2 + x + 1
(ii) x4 + x3 + x2 + x + 1
Ans: Let p(x) = x4 + x3 + x2 + x + 1
The zero of x + 1 is -1. . [x + 1= 0 means x = -1]
p(−1) = (−1)4 + (−1)3 + (−1)2 + (−1) + 1
= 1 − 1 + 1 − 1 + 1
= 1 ≠ 0
∴ By factor theorem, x+1 is not a factor of x4 + x3 + x2 + x + 1
(iii) x4 + 3x3 + 3x2 + x + 1
Ans: Let p(x)= x4 + x3 + x2 + x + 1
The zero of x+1 is -1.
p(−1)=(−1)4+3(−1)3+3(−1)2+(−1)+1
=1−3+3−1+1
=1 ≠ 0
∴ By factor theorem, x + 1 is not a factor of x4 +3x3 + 3x2 + x + 1
(iv) x3 – x2– (2+√2)x +√2
Ans: Let p(x) = x3–x2–(2+√2)x +√2
The zero of x+1 is -1.
p(−1) = (-1)3–(-1)2–(2+√2)(-1) + √2 = −1−1+2+√2+√2
= 2√2 ≠ 0
∴ By factor theorem, x+1 is not a factor of x3–x2–(2+√2)x +√2
Q2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x3 + x2 – 2x – 1, g(x) = x + 1
Ans: p(x) = 2x3+x2–2x–1, g(x) = x+1
g(x) = 0
⇒ x+1 = 0
⇒ x = −1
∴ Zero of g(x) is -1.
Now,
p(−1) = 2(−1)3+(−1)2–2(−1)–1
= −2 + 1 + 2 − 1
= 0
∴ By factor theorem, g(x) is a factor of p(x).
(ii) p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
Ans: p(x) = x3+ 3x2 3x + 1, g(x) = x + 2
g(x) = 0
⇒ x + 2 = 0
⇒ x = −2
∴ Zero of g(x) is -2.
Now,
p(−2) = (−2)3+3(−2)2+3(−2)+1
= −8 + 12 − 6 + 1
= −1 ≠ 0
∴ By factor theorem, g(x) is not a factor of p(x).
(iii) p(x)= x3 – 4x2 + x + 6, g(x) = x – 3
Ans: p(x) = x3– 4x2 + x + 6, g(x) = x - 3
g(x) = 0
⇒ x−3 = 0
⇒ x = 3
∴ Zero of g(x) is 3.
Now,
p(3) = (3)3−4(3)2 + (3) + 6
= 27 − 36 + 3 + 6
= 0
∴ By factor theorem, g(x) is a factor of p(x).
Q3. Find the value of k, if x–1 is a factor of p(x) in each of the following cases:
(i) p(x) = x2 + x + k
Ans: If x - 1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ (1)2+(1)+k = 0
⇒ 1+1+k = 0
⇒ 2+k = 0
⇒ k = −2
(ii) p(x) = 2x2 + kx + √2
Ans: If x-1 is a factor of p(x), then p(1)=0
⇒ 2(1)2 + k(1) + √2 = 0
⇒ 2 + k + √2 = 0
⇒ k = −(2 + √2)
(iii) p(x) = kx2–√2x + 1
Ans: If x - 1 is a factor of p(x), then p(1)=0
By Factor Theorem
⇒ k(1)2-√2(1)+1=0
⇒ k = √2-1
(iv) p(x) = kx2 – 3x + k
Ans: If x-1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ k(1)2–3(1)+k = 0
⇒ k−3+k = 0
⇒ 2k−3 = 0
⇒ k= 3/2
Q4. Factorize:
(i) 12x2 – 7x + 1
Ans: Using the splitting the middle term method,
We have to find a number whose sum = -7 and product =1×12 = 12
We get -3 and -4 as the numbers [-3+-4=-7 and -3×-4 = 12]
12x2–7x+1= 12x2-4x-3x+1
= 4x(3x-1)-1(3x-1)
= (4x-1)(3x-1)
(ii) 2x2 + 7x + 3
Ans: Using the splitting the middle term method,
We have to find a number whose sum = 7 and product = 2×3 = 6
We get 6 and 1 as the numbers [6+1 = 7 and 6×1 = 6]
2x2+7x+3 = 2x2+6x+1x+3
= 2x (x+3)+1(x+3)
= (2x+1)(x+3)
(iii) 6x2 + 5x - 6
Ans: Using the splitting the middle term method,
We have to find a number whose sum = 5 and product = 6×-6 = -36
We get -4 and 9 as the numbers [-4+9 = 5 and -4×9 = -36]
6x2+5x-6 = 6x2+9x–4x–6
= 3x(2x+3)–2(2x+3)
= (2x+3)(3x–2)
(iv) 3x2–x–4
Ans: Using the splitting the middle term method,
We have to find a number whose sum = -1 and product = 3 × -4 = -12
We get -4 and 3 as the numbers [-4 + 3 = -1 and -4 × 3 = -12]
3x2 – x – 4 = 3x2 – x – 4
= 3x2 – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4)
= (3x – 4)(x + 1)
5. Factorize:
(i) x3– 2x2 – x + 2
Ans: Let p(x) = x3–2x2–x+2
Factors of 2 are ±1 and ± 2
Now,
p(x) = x3–2x2–x+2
p(−1) = (−1)3–2(−1)2–(−1)+2
= −1−2+1+2
= 0
Therefore, (x+1) is the factor of p(x)
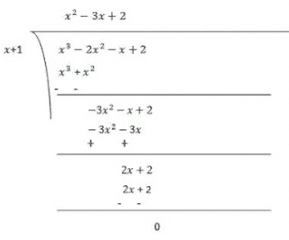
Now, Dividend = Divisor × Quotient + Remainder
Now by splitting the middle term method,
(x+1)(x2–3x+2) = (x+1)(x2–x–2x+2)
= (x+1)(x(x−1)−2(x−1))
= (x+1)(x−1)(x-2)
(ii) x3 – 3x2 – 9x – 5
Ans: Let p(x) = x3–3x2–9x–5
Factors of 5 are ±1 and ±5
By trial method, we find that
p(5) = 0
So, (x-5) is factor of p(x)
Now,
p(x) = x3–3x2–9x–5
p(5) = (5)3–3(5)2–9(5)–5
= 125−75−45−5
= 0
Therefore, (x-5) is the factor of p(x)
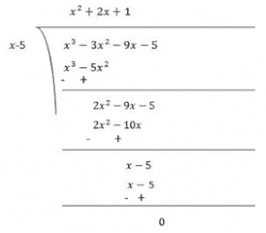
Now, Dividend = Divisor × Quotient + Remainder
(x−5)(x2+2x+1) = (x−5)(x2+x+x+1)
= (x−5)(x(x+1)+1(x+1))
= (x−5)(x+1)(x+1)
(iii) x3 + 13x2 + 32x + 20
Ans: Let p(x) = x3+13x2+32x+20
Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
By trial method, we find that
p(-1) = 0
So, (x+1) is factor of p(x)
Now,
p(x)= x3+13x2+32x+20
p(-1) = (−1)3+13(−1)2+32(−1)+20
= −1+13−32+20
= 0
Therefore, (x+1) is the factor of p(x)
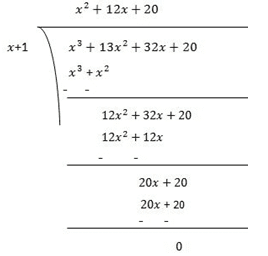
Now, Dividend = Divisor × Quotient +Remainder
Now by splitting the middle term method,
(x+1)(x2+12x+20) = (x+1)(x2+2x+10x+20)
= (x−5)x(x+2)+10(x+2)
= (x−5)(x+2)(x+10)
(iv) 2y3 + y2 – 2y – 1
Ans: Let p(y) = 2y3+y2–2y–1
Factors = 2×(−1)= -2 are ±1 and ±2
By trial method, we find that
p(1) = 0
So, (y-1) is factor of p(y)
Now,
p(y) = 2y3+y2–2y–1
p(1) = 2(1)3+(1)2–2(1)–1
= 2+1−2
= 0
Therefore, (y-1) is the factor of p(y)
Now, Dividend = Divisor × Quotient + Remainder
Now by splitting the middle term method,
(y−1)(2y2+3y+1) = (y−1)(2y2+2y+y+1)
= (y−1)(2y(y+1)+1(y+1))
= (y−1)(2y+1)(y+1)
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Solutions for Class 10 Maths - Polynomials Exercise 2.3
| 1. What are polynomials? |  |
| 2. What is the degree of a polynomial? |  |
| 3. How can we add or subtract polynomials? |  |
| 4. What is synthetic division? |  |
| 5. How do we find the zeroes of a polynomial? |  |






















