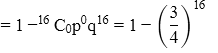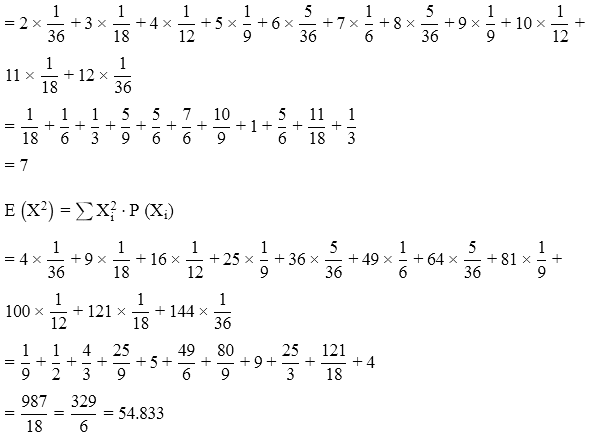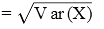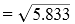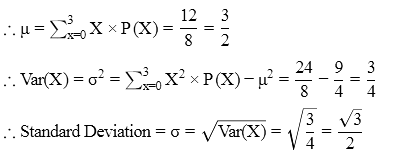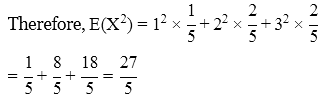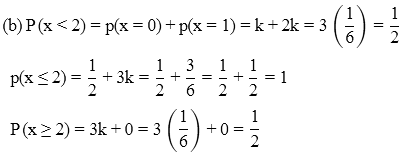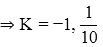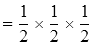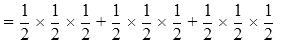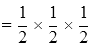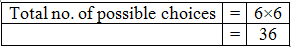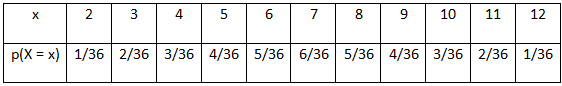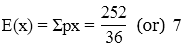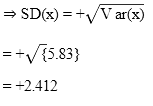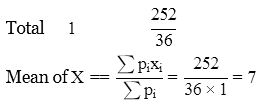Examples: Mean & Variance of Random Variables | Applied Mathematics for Class 12 - Commerce PDF Download
Example 1: The mean and variance of a binomial distribution are 4 and 3 respectively. Fix the distribution and find P(X ≥ 1).
Fact: In binomial distribution , mean = np and variance = npq
Here given np = 4 and npq = 3
So q = 3/4 ⇒ p = 1 − p = 1/4
Thus n = 16
Hence P(X ≥ 1) = 1−P(X = 0)
Example 2: Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.
When two fair dice are rolled, 6 × 6 = 36 observations are obtained.
P(X = 2) = P(1, 1) = 1/36
P(X = 3) = P(1, 2) + P(2, 1) = 2/36 = 1/18
P(X = 4)= P (1, 3) + P(2, 2) + P(3, 1) = 3/36 = 1/12
P(X = 5) = P(1, 4) + P(2, 3) + P(3, 2) + P(4, 1) = 4/36 = 1/9
P(X = 6) = P(1, 5) + P(2, 4) + P(3, 3) + P(4, 2) + P(5, 1) = 5/36
P(X = 7) = P(1, 6) + P(2, 5) + P(3, 4) + P(4, 3) + P(5, 2) + P(6, 1) = 6/36 = 1/6
P(X = 8) = P(2, 6) + P(3, 5) + P(4, 4) + P(5, 3) + P(6, 2) = 5/36
P(X = 9) = P(3, 6) + P(4, 5) + P(5, 4) + P(6, 3) = 4/36 = 1/9
P(X = 10) = P(4, 6) + P(5, 5) + P(6, 4) = 3/36 = 1/12
P(X = 11) = P(5, 6) + P(6, 5) = 2/36 = 1/18
P(X = 12) = P(6,6) = 1/36
Therefore, the required probability distribution is as follows.
Then, E(X) = ∑Xi ⋅P(Xi)
Then, Var(X) = E(X2)−[E(X)]2
= 54.833 − (7)2
= 54.833 − 49
= 5.833
∴ Standard deviation
= 2.415
Example 3: Find the variance and standard deviation of the random variable X whose probability distribution is given below: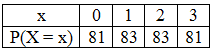
Let mean of X be μ
These are the required answers.
Example 4: The probability mass function (p.m.f) of X is given below:
We know, E(X2) = ∑X2 P(X)
Example 5: The random variable X has probability distribution P(X) of the following form.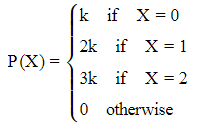 (a) determine value of K
(a) determine value of K
(b) Find P(X < 2),P(X ≤ 2),P(X ≥ 2)
(a) As Sum of all probabilities should be
⇒ k + 2k + 3k = 1 ⇒ k = 1/6
Example 6: The probability distribution of a random variable X is given below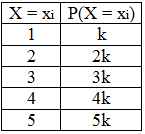 Find the value of k and the mean and variance of X.
Find the value of k and the mean and variance of X.
As we know that
∑Pi = 1
∴ k + 2k + 3k + 4k + 5k = 1
⇒ k = 1/15
Thus the value of k is 1/15
Example 7: A random variable 'X' has the following probability distribution: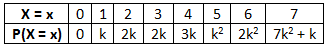 Find:
Find:
(i) k
(ii) The Mean and
(iii) P(0 < X < 5)
Sum of all probabilities must be equal to 1
So we get K + 2K + 2K + 3K + K2 + 2K2 + 7K2 + K = 1
⇒ 10K2 + 9K = 1
But probability cannot be negative , therefore the value of K= 1/10
The mean is 1.K + 2.2K + 3.2K + 4.3K + 5K2 + 6.2K2 + 7.7K2 + 7K
= 30K + 66K2 = 3 + 0.66 = 3.66
P(0 < x < 5) = P(x = 1) + P(x = 2) + P(x = 3) + P(x = 4) = K + 2K + 2K + 3K = 8K = 0.8
Example 8: Find the mean number of heads in three tosses of a fair coin.
Let X denote the success of getting heads.
Therefore, the sample space is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
It can be seen that X can take the value of 0, 1, 2 or 3.
∴ P(X = 0) = P(TTT)
=P(T)⋅P(T)⋅P(T)
= 1/8
∴ P(X = 1) = P(HHT) + P(HTH) + P(THH)
= 3/8
∴ P(X = 2) = P(HHT) + P(HTH) + P(THH)
= 3/8
∴ P(X = 3) = P(HHH)
= 1/8
Therefore, the required probability distribution is as follows.
Mean of XE(X), μ = ∑XiP(Xi)
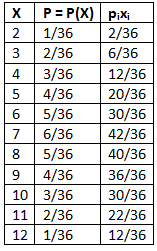
Example 9: Two unbiased dice are thrown together at random. Find the expected value of the total number of points shown up.
Let "x" indicate the sum of the points on the two dice
[Since you are required to find the expected value the sum of the scores on the two dice, the variable would represent the sum of the points on the dice]
The sum of the points on the two dice would be
2 if the dice show up {(1,1)}
3 if the dice show up {(1,2),(2,1)}
4 if the dice show up {(1,3),(2,2),(3,1)}
5 if the dice show up {(1,4),(2,3),(3,2),(4,1)}
6 if the dice show up {(1,5),(2,4),(3,3),(4,2),(5,1)}
7 if the dice show up {(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}
8 if the dice show up {(2,6),(3,5),(4,4),(5,3),(6,2)}
9 if the dice show up {(3,6),(4,5),(5,4),(6,3)}
10 if the dice show up {(4,6),(5,5),(6,4)}
11 if the dice show up {(5,6),(6,5)}
12 if the dice show up {(6,6)}
⇒ The values carried by the variable ("x") would be either 1,2,3,...,12
⇒ "X" is a discrete random variable with range = {1,2,3,...,12}
"X" represents the random variable and P(X = x) represents the probability that the value within the range of the random variable is a specified value of "x"
In the experiment of tossing 2 dice
Detailed calculation for mean and variance table is shown above:
Variance of the sum of the points on the two diceStandard Deviation of the sum of the points on the dice
Example 10: Let a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean of X .
P(X = 2) = P(1, 1) = 1/36
P(X = 3) = P[(1, 2),(2, 1)] = 2/36
P(X = 4) = P[(1, 3), (2, 2), (3, 1)] = 3/36
P(X = 5) = P[(1, 4),( 2, 3), (3, 2),(4, 1)] = 4/36
P(X = 6) = P[(1, 5), (2, 4),(3, 3),(4, 2),(5, 1)] =5/36
P(X = 7) = P[(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)] =6/36
P(X = 8) = P[(2, 6 ,(3, 5), (4, 4), (5, 3), (6, 2)] = 5/36
P(X = 9) = P[(3, 6), (4, 5), (5, 4), (6, 3)] = 4/36
P(X = 10) = P[(4, 6), (5, 5), (6, 4)] = 3/36
P(X = 11) = P[(5, 6),(6, 5)] = 2/36
P(X = 12) = P[(6, 6)] = 1/36
Mean = 7
Example 11:If a coin is tossed 5 times, find the probability of:
(a) Exactly 2 heads
(b) At least 4 heads.
(a) The repeated tossing of the coin is an example of a Bernoulli trial. According to the problem:
Number of trials: n = 5
Probability of head: p = 1/2 and hence the probability of tail, q = 1/2
For exactly two heads:
x = 2
P(x = 2) = 5C2 p2 q5-2 = 5! / 2! 3! × (½)2 × (½)3
P(x = 2) = 5/16
(b) For at least four heads,
x ≥ 4, P(x ≥ 4) = P(x = 4) + P(x=5)
Hence,
P(x = 4) = 5C4 p4 q5-4 = 5!/4! 1! × (½)4 × (½)1 = 5/32
P(x = 5) = 5C5 p5 q5-5 = (½)5 = 1/32
Therefore,
P(x ≥ 4) = 5/32 + 1/32 = 6/32 = 3/16
Example 12: For the same question given above, find the probability of:
(a) Getting at least 2 heads
P (at most 2 heads) = P(X ≤ 2) = P (X = 0) + P (X = 1)
P(X = 0) = (½)5 = 1/32
P(X=1) = 5C1 (½)5. = 5/32
Therefore,
P(X ≤ 2) = 1/32 + 5/32 = 3/16
Example 13: A fair coin is tossed 10 times, what are the probability of getting exactly 6 heads and at least six heads.
Let x denote the number of heads in an experiment.
Here, the number of times the coin tossed is 10. Hence, n = 10.
The probability of getting head, p ½
The probability of getting a tail, q = 1-p = 1-(½) = ½.
The binomial distribution is given by the formula:
P(X= x) = nCxpxqn-x, where = 0, 1, 2, 3, …
Therefore, P(X = x) = 10Cx(½)x(½)10-x
(i) The probability of getting exactly 6 heads is:
P(X=6) = 10C6(½)6(½)10-6
P(X= 6) = 10C6(½)10
P(X = 6) = 105/512.
Hence, the probability of getting exactly 6 heads is 105/512.
(ii) The probability of getting at least 6 heads is P(X ≥ 6)
P(X ≥ 6) = P(X=6) + P(X=7) + P(X= 8) + P(X = 9) + P(X=10)
P(X ≥ 6) = 10C6(½)10 + 10C7(½)10 + 10C8(½)10 + 10C9(½)10 + 10C10(½)10
P(X ≥ 6) = 193/512.
|
64 videos|110 docs|63 tests
|