Q.1. Prove that √5 is irrational.
Solutions: Let us assume, that √5 is rational number.
i.e. √5 = x/y (where, x and y are co-primes)
y√5= x
Squaring both the sides, we get,
(y√5)2 = x2
⇒ 5y2 = x2……………………………….. (1)
Thus, x2 is divisible by 5, so x is also divisible by 5.
Let us say, x = 5k, for some value of k and substituting the value of x in equation (1), we get,
5y2 = (5k)2
⇒ y2 = 5k2
is divisible by 5 it means y is divisible by 5.
Clearly, x and y are not co-primes. Thus, our assumption about √5 is rational is incorrect.
Hence, √5 is an irrational number.

Q.2. Prove that 3 + 2√5 + is irrational.
Solutions: Let us assume 3 + 2√5 is rational.
Then we can find co-prime x and y (y ≠ 0) such that 3 + 2√5 = x/y
Rearranging, we get,
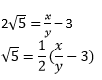
Since, x and y are integers, thus,
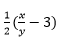 is a rational number.
is a rational number.
Therefore, √5 is also a rational number. But this contradicts the fact that √5 is irrational.
So, we conclude that 3 + 2√5 is irrational.
Q.3. Prove that the following are irrationals:
(i) 1/√2
(ii) 7√5
(iii) 6 + √2
Solutions:
(i) 1/√2
Let us assume 1/√2 is rational.
Then we can find co-prime x and y (y ≠ 0) such that 1/√2 = x/y
Rearranging, we get,
√2 = y/x
Since, x and y are integers, thus, √2 is a rational number, which contradicts the fact that √2 is irrational.
Hence, we can conclude that 1/√2 is irrational.
(ii) 7√5
Let us assume 7√5 is a rational number.
Then we can find co-prime a and b (b ≠ 0) such that 7√5 = x/y
Rearranging, we get,
√5 = x/7y
Since, x and y are integers, thus, √5 is a rational number, which contradicts the fact that √5 is irrational.
Hence, we can conclude that 7√5 is irrational.
(iii) 6 +√2
Let us assume 6 +√2 is a rational number.
Then we can find co-primes x and y (y ≠ 0) such that 6 +√2 = x/y⋅
Rearranging, we get,
√2 = (x/y) – 6
Since, x and y are integers, thus (x/y) – 6 is a rational number and therefore, √2 is rational. This contradicts the fact that √2 is an irrational number.
Hence, we can conclude that 6 +√2 is irrational.

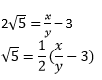
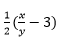 is a rational number.
is a rational number.


























