NCERT Solutions for Class 9 Maths Chapter 7 - Exercise 7.4 and 7.5 Triangles
Exercise 7.4
Q.1. Show that in a right-angled triangle, the hypotenuse is the longest side.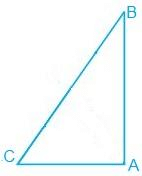
Solution:
It is known that ABC is a triangle right angled at B.
We know that,
A + B + C = 180°
Now, if B + C = 90° then A has to be 90°.
Since A is the largest angle of the triangle, the side opposite to it must be the largest.
So, AB is the hypotenuse which will be the largest side of the above right-angled triangle i.e. ΔABC.
Q.2. In Fig. 7.48, sides AB and AC of ΔABC are extended to points P and Q, respectively. Also, PBC < QCB. Show that AC > AB.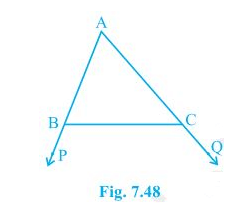
Solution:
It is given that PBC < QCB
We know that ABC + PBC = 180°
So, ABC = 180°-PBC
Also,
ACB + QCB = 180°
Therefore ACB = 180° -QCB
Now, since PBC < QCB,
∴ ABC > ACB
Hence, AC > AB as sides opposite to the larger angle is always larger.
Q.3. In Fig. 7.49, B < A and C < D. Show that AD < BC.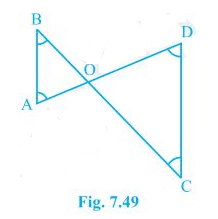
Solution:
In the question, it is mentioned that angles B and angle C is smaller than angles A and D, respectively i.e. B < A and C < D.
Now,
Since the side opposite to the smaller angle is always smaller
AO < BO — (i)
And OD < OC —(ii)
By adding equation (i) and equation (ii) we get
AO + OD < BO + OC
So, AD < BC
Q.4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50). Show that A > C and B > D.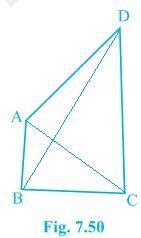
Solution:
In ΔABD, we see that
AB < AD < BD
So, ADB < ABD — (i) (Since angle opposite to longer side is always larger)
Now, in ΔBCD,
BC < DC < BD
Hence, it can be concluded that
BDC < CBD — (ii)
Now, by adding equation (i) and equation (ii) we get,
ADB + BDC < ABD + CBD
ADC < ABC
B > D
Similarly, In triangle ABC,
ACB < BAC — (iii) (Since the angle opposite to the longer side is always larger)
Now, In ΔADC,
DCA < DAC — (iv)
By adding equation (iii) and equation (iv) we get,
ACB + DCA < BAC+DAC
⇒ BCD < BAD
∴ A > C
Q.5. In Fig 7.51, PR > PQ and PS bisect QPR. Prove that PSR > PSQ.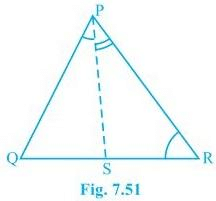
Solution:
It is given that PR > PQ and PS bisects QPR
Now we will have to prove that angle PSR is smaller than PSQ i.e. PSR > PSQ
Proof:
QPS = RPS — (ii) (As PS bisects ∠QPR)
PQR > PRQ — (i) (Since PR > PQ as angle opposite to the larger side is always larger)
PSR = PQR + QPS — (iii) (Since the exterior angle of a triangle equals to the sum of opposite interior angles)
PSQ = PRQ + RPS — (iv) (As the exterior angle of a triangle equals to the sum of opposite interior angles)
By adding (i) and (ii)
PQR + QPS > PRQ + RPS
Thus, from (i), (ii), (iii) and (iv), we get
PSR > PSQ
Q.6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Solution:
First, let “l” be a line segment and “B” be a point lying on it. A line AB perpendicular to l is now drawn. Also, let C be any other point on l. The diagram will be as follows: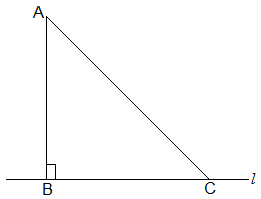 To prove:
To prove:
AB < AC
Proof:
In ΔABC, B = 90°
Now, we know that
A + B + C = 180°
∴ A + C = 90°
Hence, C must be an acute angle which implies C < B
So, AB < AC (As the side opposite to the larger angle is always larger)
Exercise 7.5
Q.1. ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
Soultion: Let us consider a ΔABC.
Draw ‘l’ the perpendicular bisector of AB.
Draw ‘m’ the perpendicular bisector of BC.
Let the two perpendicular bisectors ‘l’ and ‘m’ meet at O. ‘O’ is the required point which is equidistant from A, B and C.
Note: If we draw a circle with centre ‘O’ and radius OB or OC, then it will pass through A, B and C.
Q.2. In a triangle, locate a point in its interior which is equidistant from all the sides of the triangle.
Solution: Let us consider a ΔABC.
Draw ‘l’ the bisector of ∠B.
Draw ‘m’ the bisector of ∠C.
Let the two bisectors l and m meet at O. Thus, ‘O’ is the required point which is equidistant from the sides of ΔABC.
required point which is equidistant from the sides of ΔABC.
Note: If we draw OM ⊥ BC and draw a circle with O as centre and OM as radius, then the circle will touch the sides of the triangle.
Q.3. In a huge park, people are concentrated at three points (see figure): A : where there are different slides and swings form children,
B : near which a man-made lake is situated, C: which is near to a large parking and exit.
Where should an ice cream parlour be set up so that maximum number of persons can approach it?
Hint: The parlour should be equidistant from A, B and C.
Solution: Let us join A and B, and draw ‘l’ the perpendicular bisector of AB.
Now, join B and C, and draw ‘m’ the perpendicular bisector of BC. Let the perpendicular bisectors ‘l’ and ‘m’ meet at ‘O’. The point ‘O’ is the required point where the ice cream parlour be set up.
Note: If we join ‘A’ and ‘C’, and draw the perpendicular bisectors, then it will also meet (or pass through) the point O.
Q.4. Complete the hexagonal and star shaped Rangolies [see Fig. (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
Solution: It is an activity. We get the 150 equilateral triangles in the figure
(i) and 300 equilateral triangles in the figure
(ii). ∴ The figure
(ii) has more triangles.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 7 - Exercise 7.4 and 7.5 Triangles
| 1. What are the properties of an isosceles triangle? |  |
| 2. How can I determine if a triangle is equilateral? |  |
| 3. What is the Pythagorean Theorem? |  |
| 4. How can I find the area of a triangle? |  |
| 5. Can a triangle have more than one obtuse angle? |  |
















